Chapter: 11th Statistics : Chapter 9 : Random Variables and Mathematical Expectation
Distribution function and its properties
Distribution
function and its properties
We
get the probability of a given event at a particular point. If we want to have
the probability upto the point we get the probability P(X
≤ x). This type of probability is known as probability mass
function. We can also find how the probability is distributed within certain
limits. [P (X < x) or P (X > x) or P (a < x < b)].
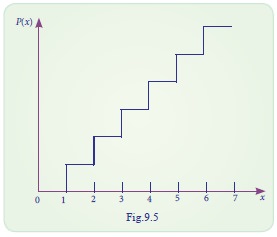
Distribution Function for discrete random variable
Definition:
Let X be a random variable ,the cumulative distribution
function (c.d.f) of a random variable X is defined as F(x)
= P(X≤x), 6x. It is called simply as
distribution function.
Properties:
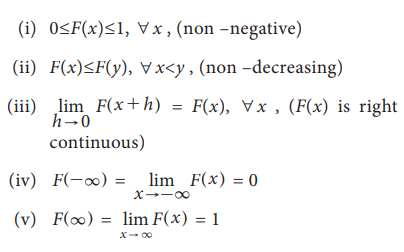
Distribution Function for continuous random variable
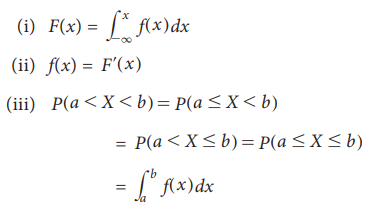
Properties

Example 9.12
A
random variable X has the following probability
mass function

i.
Find the value of ‘a ’
ii.
Find the c.d.f F(x) of X
iii.
Evaluate : (a) P(X
≥ 4) (b) P(X < 5) (c) P(3 ≤ X ≤6)
iv. P(X = 5) using F(x)
Solution:

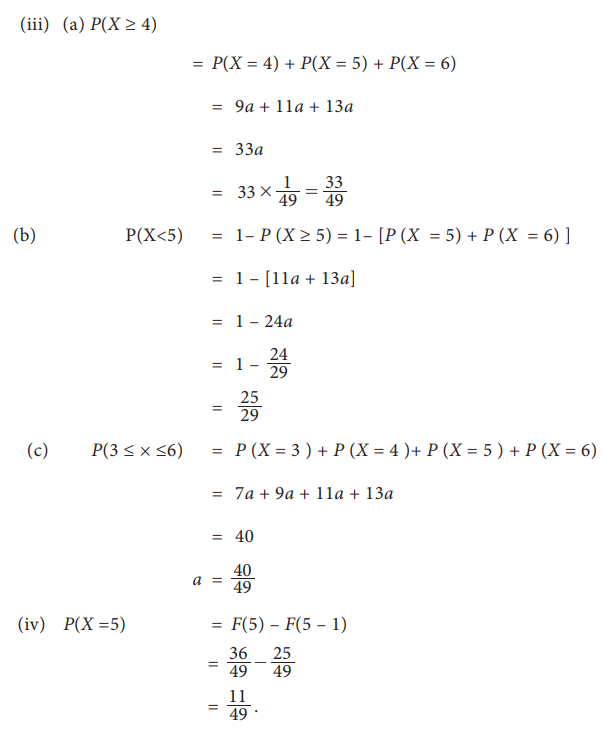
Example 9.13
Let
X be a random variable with p.d.f

Solution:
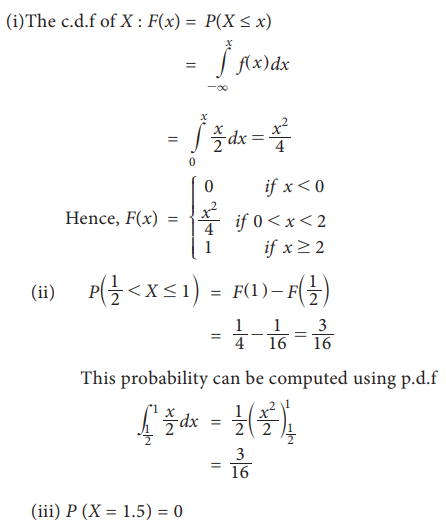
Related Topics