Principle of frequency modulation

Principle of frequency modulation

Frequency modulation uses the information signal, V_m(t) to vary the carrier frequency within some small range about its original value. Here are the three signals in mathematical form:

Information: V_m(t)

Carrier: V_c(t) = V_co sin ( 2 p f_c t + f )

FM: V_FM (t) = V_co sin (2 p [f_c + (Df/V_mo) V_m (t) ] t + f)

We have replaced the carrier frequency term, with a time-varying frequency. We have also introduced a new term: Df, the peak frequency deviation. In this form, you should be able to see that the carrier frequency term: f_c + (Df/V_mo) V_m (t) now varies between the extremes of f_c - Df and f_c + Df. The interpretation of Df becomes clear: it is the farthest away from the original frequency that the FM signal can be. Sometimes it is referred to as the "swing" in the frequency.

We can also define a modulation index for FM, analogous to AM: b = Df/f_m , where f_m is the maximum modulating frequency used.

The simplest interpretation of the modulation index, b, is as a measure of the peak frequency deviation, Df. In other words, b represents a way to express the peak deviation frequency as a multiple of the maximum modulating frequency, f_m, i.e. Df = b f_m.

Example: suppose in FM radio that the audio signal to be transmitted ranges from 20 to 15,000 Hz (it does). If the FM system used a maximum modulating index, b, of 5.0, then the frequency would "swing" by a maximum of 5 x 15 kHz = 75 kHz above and below the carrier frequency.

Here is a simple FM signal:

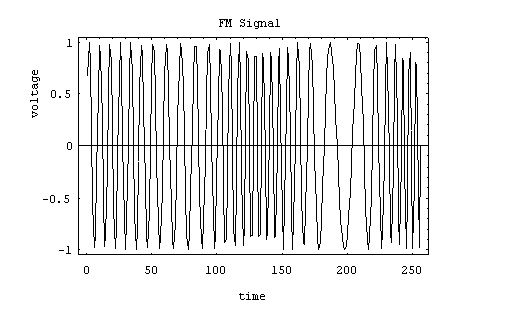
Here, the carrier is at 30 Hz, and the modulating frequency is 5 Hz. The modulation index is about 3, making the peak frequency deviation about 15 Hz. That means the frequency will vary somewhere between 15 and 45 Hz. How fast the cycle is completed is a function of the modulating frequency.

FM Spectrum

A spectrum represents the relative amounts of different frequency components in any signal. Its like the display on the graphic-equalizer in your stereo which has leds showing the relative amounts of bass, midrange and treble. These correspond directly to increasing frequencies (treble being the high frequency components). It is a well-know fact of mathematics, that any function (signal) can be decomposed into purely sinusoidal components (with a few pathological exceptions) . In technical terms, the sines and cosines form a complete set of functions, also known as a basis in the infinite-dimensional vector space of real-valued functions (gag reflex). Given that any signal can be thought to be made up of sinusoidal signals, the spectrum then represents the "recipe card" of how to make the signal from sinusoids. Like: 1 part of 50 Hz and 2 parts of 200 Hz. Pure sinusoids have the simplest spectrum of all, just one component:

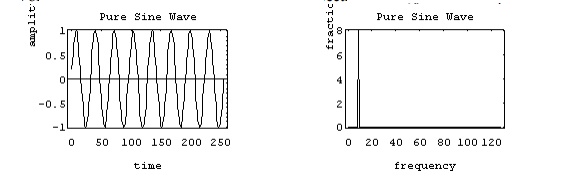
In this example, the carrier has 8 Hz and so the spectrum has a single component with value 1.0 at 8 Hz

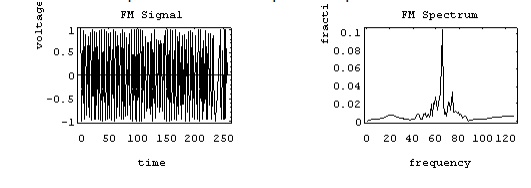
The FM spectrum is considerably more complicated. The spectrum of a simple FM signal looks like:

The carrier is now 65 Hz, the modulating signal is a pure 5 Hz tone, and the modulation index is 2. What we see are multiple side-bands (spikes at other than the carrier frequency) separated by the modulating frequency, 5 Hz. There are roughly 3 side-bands on either side of the carrier. The shape of the spectrum may be explained using a simple heterodyne argument: when you mix the three frequencies (f_c, f_m and Df) together you get the sum and difference frequencies. The largest combination is f_c + f_m + Df, and the smallest is f_c - f_m - Df. Since Df = b f_m, the frequency varies (b + 1) f_m above and below the carrier.

A more realistic example is to use an audio spectrum to provide the modulation:

In this example, the information signal varies between 1 and 11 Hz. The carrier is at 65 Hz and the modulation index is 2. The individual side-band spikes are replaced by a more-or-less continuous spectrum. However, the extent of the side-bands is limited (approximately) to (b + 1) f_m above and below. Here, that would be 33 Hz above and below, making the bandwidth about 66 Hz. We see the side-bands extend from 35 to 90 Hz, so out observed bandwidth is 65 Hz.

You may have wondered why we ignored the smooth humps at the extreme ends of the spectrum. The truth is that they are in fact a by-product of frequency modulation (there is no random noise in this example). However, they may be safely ignored because they are have only a minute fraction of the total power. In practice, the random noise would obscure them anyway.

Example: FM Radio

FM radio uses frequency modulation, of course. The frequency band for FM radio is about 88 to 108 MHz. The information signal is music and voice which falls in the audio spectrum. The full audio spectrum ranges form 20 to 20,000 Hz, but FM radio limits the upper modulating requency to 15 kHz (cf. AM radio which limits the upper frequency to 5 kHz). Although, some of the signal may be lost above 15 kHz, most people can't hear it anyway, so there is little loss of fidelity. FM radio maybe appropriately referred to as "high-fidelity."

If FM transmitters use a maximum modulation index of about 5.0, so the resulting bandwidth is 180 kHz (roughly 0.2 MHz). The FCC assigns stations ) 0.2 MHz apart to prevent overlapping signals (coincidence? I think not!). If you were to fill up the FM band with stations, you could get 108 - 88 / .2 = 100 stations, about the same number as AM radio (107). This sounds convincing, but is actually more complicated (agh!).

FM radio is broadcast in stereo, meaning two channels of information. In practice, they generate three signals prior to applying the modulation:

the L + R (left + right) signal in the range of 50 to 15,000 Hz. a 19 kHz pilot carrier.

the L-R signal centered on a 38 kHz pilot carrier (which is suppressed) that ranges from 23 to 53 kHz .

So, the information signal actually has a maximum modulating frequency of 53 kHz, requiring a reduction in the modulation index to about 1.0 to keep the total signal bandwidth about 200 kHz.

FM Performance

Bandwidth

As we have already shown, the bandwidth of a FM signal may be predicted using:

BW = 2 (b + 1 ) f_m

where b is the modulation index and

f_m is the maximum modulating frequency used.

FM radio has a significantly larger bandwidth than AM radio, but the FM radio band is also larger. The combination keeps the number of available channels about the same.

The bandwidth of an FM signal has a more complicated dependency than in the AM case (recall, the bandwidth of AM signals depend only on the maximum modulation frequency). In FM, both the modulation index and the modulating frequency affect the bandwidth. As the information is made stronger, the bandwidth also grows.

Efficiency

The efficiency of a signal is the power in the side-bands as a fraction of the total. In FM signals, because of the considerable side-bands produced, the efficiency is generally high. Recall that conventional AM is limited to about 33 % efficiency to prevent distortion in the receiver when the modulation index was greater than 1. FM has no analogous problem.

The side-band structure is fairly complicated, but it is safe to say that the efficiency is generally improved by making the modulation index larger (as it should be). But if you make the modulation index larger, so make the bandwidth larger (unlike AM) which has its disadvantages. As is typical in engineering, a compromise between efficiency and performance is struck. The modulation index is normally limited to a value between 1 and 5, depending on the application.

Noise

FM systems are far better at rejecting noise than AM systems. Noise generally is spread uniformly across the spectrum (the so-called white noise, meaning wide spectrum). The amplitude of the noise varies randomly at these frequencies. The change in amplitude can actually modulate the signal and be picked up in the AM system. As a result, AM systems are very sensitive to random noise. An example might be ignition system noise in your car. Special filters need to be installed to keep the interference out of your car radio.

FM systems are inherently immune to random noise. In order for the noise to interfere, it would have to modulate the frequency somehow. But the noise is distributed uniformly in frequency and varies mostly in amplitude. As a result, there is virtually no interference picked up in the FM receiver. FM is sometimes called "static free, " referring to its superior immunity to random noise.