Performance of Wind Machines

PERFORMANCE OF WIND MACHINES

WECS efficiency is of interest to both aerogenerator designers and system engineers. As WECS is a capital intensive technology, it is desirable for the overall wind electric plant to have the highest efficiency possible, thus optimally utilizing capital resources and minimizing the busbar electric energy cost.

The overall conversion efficiency, µ_oof an aerogenerator of the general type is

Above equation shows an application of cascaded energy conversion, from which overall efficiency will be strongly determined by the lowest efficiency converter in the cascade. For the aerogenerator this is the aeroturbine; the efficiency of the remaining three elements can be made quite high but less than 100 percent. It is now evident why so much emphasis is placed on the efficiency of the aeroturbine in wind literature.

Consider an arbitrary aeroturbine (Here Aero turbine is not equal to aerogenerator) of cross-sectional area ‘A’ driven by the wind. Its efficiency would be:

Thus the coefficient of performance of an aeroturbine is the fraction of power in the wind through the swept area which is converted into useful mechanical shaft power. The coefficient of performance is widely utilized throughout the recent wind research. We have seen that C_p for horizontal axis wind machine has theoretical maximum value = 0.593.

This theoretical efficiency limitation on a wind energy conversion system is loosely analogical similar to the thermodynamic carnot efficiency limitation on a conventional thermal power plant.

We know that the convertible power of energy is proportional to the cube of the wind speed. Thus if the wind speed decreases by 20%, the power output is reduced by almost 50%. The wind speed may very considerable from day to day and from season to season. The efficiency of a wind generator depends on the design of an wind rotor and rotational speed, expressed as the ratio of blade tip speed to wind speed i.e., V_T/V (is called as TSR – Tip Speed Ratio), if n is the rotation frequency, ie., rotation per second, if a rotor diameter D meters, the tip speed is πnD m/sec.

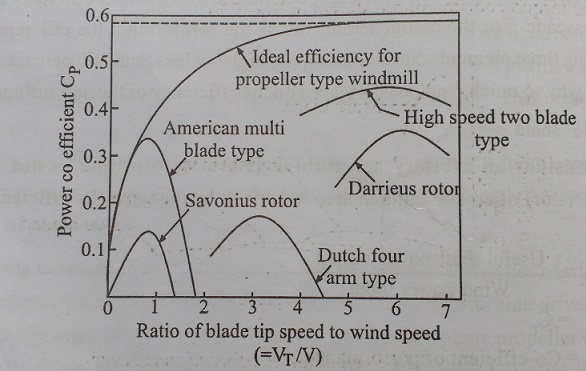
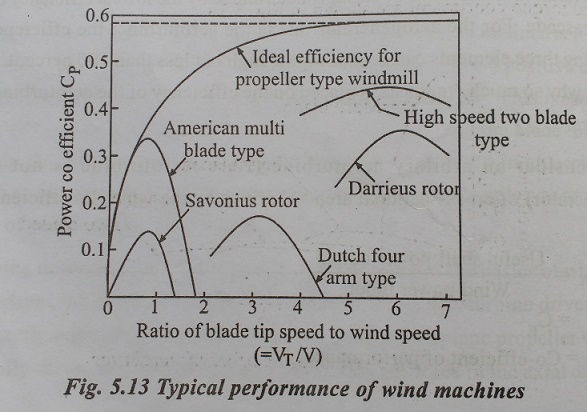
The dependence of the power coefficient on the tip speed ratio (TSR) for some common rotor types is indicated in Fig. 5.13. It is seen that the two-bladed propeller type of rotor can attain a much higher power coefficient (i.e., it is more efficient) than the American multi-blade wind mill and the classical Dutch four-bladed windmill. In practice two-bladed propeller (horizontal axis) rotor are ound to attain a maximum power coefficient of 0.40 to 0.45 at a tip speed ratio in the range a roughly 6 to 10

Golding has derived the expression for aeroturbine efficiency as,

Clearly If there were no drag, i.e., K=0, then efficiency would be unity (μ_A=1). In actuality K can be made very small, depending on the airfoil choosen and the angle of attack. Also above equation tells us the efficiency would be low if V_T/V were very large or again If it were small. One suspicions that there exists an optimum ratio of V_T/V (i.e., TSR).

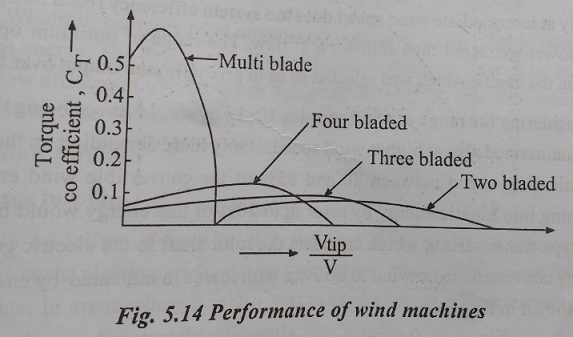
If one assembles models of various types of aeroturbine blades and puts them in a wind tunnel and runs carefully controlled experiments of their efficiencies as function of their TSR’S, then one obtains a family of curves similar to that shown in Fig.5.14.

The various types of windmills performance characteristics with respect to TSR and torque coefficient are shown in Fig. 5.14.

Only at intermediate wind speed does the system efficiency reach its optimum and the power extracted then follows a V³ law. The range of optimum operation depends on the engine which was selected so as to give optimum output over the year.

Considering the range of wind speed is 10-14m/sec, 14m/sec being the rated velocity maintained also at higher wind speeds. Only there depending on the degree of sophistication, could between 70 and 85% of the convertible wind energy by the gear type transmission, which connects the rotor shaft to the electric generator. The energy conversion from wind to utilities with losses in indicated by energy flow diagram shown in Fig. 5.15.