Paths: Their Role in White Box-Based Test Design

Paths: Their Role in White Box-Based Test Design

In Section 5.2 the role of a control flow graph as an aid to white box test design was described. It was also mentioned that tools were available to generate control flow graphs. These tools typically calculate a value for a software attribute called McCabe‘s Cyclomatic Complexity V(G) from a flow graph. The cyclomatic complexity attribute is very useful to a tester. The complexity value is usually calculated from the control flow graph (G) by the formula

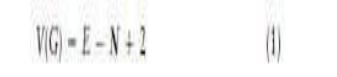
The value E is the number of edges in the control flow graph and N is the number of nodes. This formula can be applied to flow graphs where there are no disconnected components [4]. As an example, the cyclomatic complexity of the flow graph in Figure 5.3 is calculated as follows:

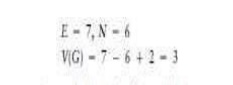
The cyclomatic complexity value of a module is useful to the tester in several ways. One of its uses is to provide an approximation of the number of test cases needed for branch coverage in a module of structured code. If the testability of a piece of software is defined in terms of the number of test cases required to adequately test it, then McCabes‘ cyclomatic complexity provides an approximation of the testability of a module. The tester can use the value of V(G) along with past project data to approximate the testing time and resources required to test a software module. In addition, the cyclomatic complexity value and the control flow graph give the tester another tool for developing white box test cases using the concept of a path. A definition for this term is given below.

A path is a sequence of control flow nodes usually beginning from the entry node of a graph through to the exit node.

A path may go through a given segment of the control flow graph one or more times. We usually designate a path by the sequence of nodes it encompasses. For example, one path from the graph in Figure 5.3 is

1-2-3-4-8

represents the edge between nodes 4 and 8 Cyclomatic complexity is a measure of the number of so-called in-dependent paths in the graph. An independent path is a special kind of path in the flow graph. Deriving a set of independent paths using a flow graph can support a tester in identifying the control flow features in the code and in setting coverage goals. A tester identifies a set of independent paths for the software unit by starting out with one simple path in the flow graph and iteratively adding new paths to the set by adding new edges at each iteration until there are no more new edges to add. The independent paths are defined as any new path through the graph that introduces a new edge that has not be traversed before the path is defined.

A set of independent paths for a graph is sometimes called a basis set. For most software modules it may be possible to derive a number of basis sets. If we examine the flow graph in Figure 5.3, we can derive the following set of independent paths starting with the first path identified above.

(i) 1-2-3-4-8

(ii)         1-2-3-4-5-6-7-4-8

(iii)1-2-3-4-5-7-4-8

The number of independent paths in a basis set is equal to the cyclomatic complexity of the graph. For this example they both have a value of 3. Recall that the cyclomatic complexity for a flow graph also gives us an approximation (usually an upper limit) of the number of tests needed to achieve branch (decision) coverage. If we prepare white box test cases so that the inputs cause the execution of all of these paths, we can be reasonably sure that we have achieved complete statement and decision coverage for the module. Testers should be aware that although identifying the independent paths and calculating cyclomatic complexity in a module of structured code provides useful support for achieving decision coverage goals, in some cases the number of independent paths in the basis set can lead to an overapproximation of the number of test cases needed for decision (branch) coverage. This is illustrated by the code example of Figure 5.2, and the test case as shown in Table 5.1.

To complete the discussion in this section, one additional logic-based testing criterion based on the path concept should be mentioned. It is the strongest program-based testing criterion, and it calls for complete path coverage; that is, every path (as distinguished from independent paths) in a module must be exerc ised by the test set at least once. This may not be a practical goal for a tester. For example, even in a small and simple unit of code there may be many paths between the entry and exit nodes. Adding even a few simple decision statements increases the number of paths.

Every loop multiplies the number of paths based on the number of possible iterations of the loop since each iteration constitutes a different path through the code. Thus, complete path coverage for even a simple module may not be practical, and for large and complex modules it is not feasible.

In addition, some paths in a program may be unachievable, that is, they cannot be executed no matter what combinations of input data are used. The latter makes achieving complete path coverage an impossible task. The same condition of unachievability may also hold true for some branches or statements in a program. Under these circumstances coverage goals are best expressed in terms of the number of feasible or achievable paths, branches, or statements respectively.

As a final note, the reader should not confuse the coverage based on independent path testing as equivalent to the strongest coverage goal—complete path coverage. The basis set is a special set of paths and does not represent all the paths in a module; it serves as a tool to aid the tester in achieving decision coverage.