Evaluating Test Adequacy Criteria

Evaluating Test Adequacy Criteria

Most of the white box testing approaches we have discussed so far are associated with application of an adequacy criterion. 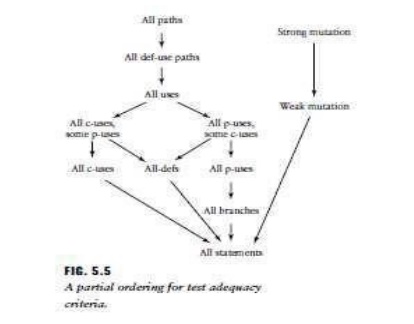Testers are often faced with the decision of which criterion to apply to a given item under test given the nature of the item and the constraints of the test environment (time, costs, resources) One source of information the tester can use to select an appropriate criterion is the test adequacy criterion hierarchy as shown in Figure 5.5 which describes a subsumes relationship among the criteria. Satisfying an adequacy criterion at the higher levels of the hierarchy implies a greater thoroughness in testing [1,14-16]. The criteria at the top of the hierarchy are said to subsume those at the lower levels. For example, achieving all definition-use (def-use) path adequacy means the tester has also achieved both branch and statement adequacy. Note from the hierarchy that statement adequacy is the weakest of the test adequacy criteria. Unfortunately, in many organizations achieving a high level of statement coverage is not even included as a minimal testing goal.

As a conscientious tester you might at first reason that your testing goal should be to develop tests that can satisfy the most stringent criterion. However, you should consider that each adequacy criterion has both strengths and weaknesses. Each, is effective in revealing certain types of defects. Application of the so-called Stronger criteria usually requires more tester time and resources. This translates into higher testing costs. Testing conditions, and the nature of the software should guide your choice of a criterion.

Support for evaluating test adequacy criteria comes from a theoretical treatment developed by Weyuker . She presents a set of axioms that allow testers to formalize properties which should be satisfied by any good program-based test data adequacy criterion. Testers can use the axioms to

• recognize both strong and weak adequacy criteria; a tester may decide to use a weak criterion, but should be aware of its weakness with respect to the properties described by the axioms;

• focus attention on the properties that an effective test data adequacy criterion should exhibit;

•  select an appropriate criterion for the item under test;

•   stimulate thought for the development of new criteria; the axioms are the framework with

which to evaluate these new criteria.

The axioms are based on the following set of assumptions :

(i) programs are written in a structured programming language;

(ii)    programs  are    SESE   (single    entry/single  exit);

(iii)  all input statements appear at the beginning of the program;

(iv)          all output statements appear at the end of the program.

The axioms/properties described by Weyuker are the following :

1. Applicability Property

For every program there exists an adequate test set. What this axiom means is that for all programs we should be able to design an adequate test set that properly tests it. The test set may be very large so the tester will want to select representable points of the specification domain to test it. If we test on all representable points, that is called an exhaustive test set. The exhaustive test set will surely be adequate since there will be no other test data that we can generate. However, in past discussions we have ruled out exhaustive testing because in most cases it is too expensive, time consuming, and impractical.

2. Non exhaustive Applicability Property

For a program P and a test set T, P is adequately tested by the test set T, and T is not an exhaustive test set. To paraphrase, a tester does not need an exhaustive test set in order to adequately test a program.

3. Monotonicity Property

If a test set T is adequate for program P, and if T is equal to, or a subset of T , then T is adequate for program P.‖

4. Inadequate Empty Set

In empty test set is not an adequate test for any program. If a program is not tested at all, a tester cannot claim it has been adequately tested! Note that these first four axioms are very general and apply to all programs independent of programming language and equally apply to uses of both program- and specification-based testing. For some of the next group of axioms this is not true.

5. Antiextensionality Property

There are programs P and Q such that P is equivalent to Q, and T is adequate for P, but T is not adequate for Q. We can interpret this axiom as saying that just because two programs are semantically equivalent (they may perform the same function) does not mean we should test them the same way. Their implementations (code structure) may be very different. The reader should note that if programs have equivalent specifications then their test sets may coincide using black box testing techniques, but this axiom applies to program-based testing and it is the differences that may occur in program code that make it necessary to test P and Q with different test sets.

6. General Multiple Change Property

There are programs P and Q that have the same shape, and there is a test set T such that T is adequate for P, but is not adequate for Q. Here Weyuker introduces the concept of shape to express a syntactic equivalence. She states that two programs are the same shape if one can be transformed into the other by applying the set of rules shown below any number of times:

(i) replace relational operator r1 in a predicate with relational operator r2;

(ii) replace constant c1 in a predicate of an assignment statement with constant c2;

(iii)replace arithmetic operator a1 in an assignment statement with arithmetic operator a2.

Axiom 5 says that semantic closeness is not sufficient to imply that two programs should be tested in the same way. Given this definition of shape, Axiom 6 says that even the syntactic closeness of two programs is not strong enough reason to imply they should be tested in the same way.

7. Antidecomposition Property

There is a program P and a component Q such that T is adequate for P, T is the set of vectors of values that variables can assume on entrance to Q for some t in T, and T is not adequate for Q.This axiom states that although an encompassing program has been adequately tested, it does not follow that each of its components parts has been properly tested. Implications for this axiom are:

a routine that has been adequately tested in one environment may not have been adequately tested to work in another environment, the environment being the enclosing program.

although we may think of P, the enclosing program, as being more complex than Q it may not be. Q may be more semantically complex; it may lie on an unexecutable path of P, and thus would have the null set, as its test set, which would violate Axiom 4.

8. Anticomposition Property

There are programs P and Q, and test set T, such that T is adequate for P, and the set of vectors of values that variables can assume on entrance to Q for inputs in T is adequate for Q, but T is not adequate for P; Q (the composition of P and Q). Paraphrasing this axiom we can say that adequately testing each individual program component in isolation does not necessarily mean that we have adequately tested the entire program (the program as a whole). When we integrate two separate program components, there are interactions that cannot arise in the isolated components. Axioms 7 and 8 have special impact on the testing of object oriented code. These issues are covered in Chapter 6.

9. Renaming Property

If P is a renaming of Q, then T is adequate for P only if T is adequate for Q. A program P is a renaming of Q if P is identical to Q expect for the fact that all instances of an identifier, let us say a in Q have been replaced in P by an identifier, let us say b, where b does not occur in Q, or if there is a set of such renamed identifiers. This axiom simply says that an inessential change in a program such as changing the names of the variables should not change the nature of the test data that are needed to adequately test the program.

10. Complexity Property

For every n, there is a program P such that P is adequately tested by a size n test set, but not by any size n 1 test set.This means that for every program, there are other programs that require more testing.

11. Statement Coverage Property

If the test set T is adequate for P, then T causes every executable statement of P to be executed.Ensuring that their test set executed all statements in a program is a minimum coverage goal for a tester. A tester soon realizes that if some portion of the program has never been executed, then that portion could contain defects: it could be totally in error and be working improperly. Testing would not be able to detect any defects in this portion of the code. However, this axiom implies that a tester needs to be able to determine which statements of a program are executable. It is possible that not all of program statements are executable. Unfortunately, there is no algorithm to support the tester in the latter task, but

Weyuker believes that developers/testers are quite good at determining whether or not code is, or is not, executable [2]. Issues relating to infeasible (unexecutable) paths, statements, and branches have been discussed.

The first eight axioms as described by Weyuker exposed weaknesses in several well -known program-based adequacy criteria. For example , both statement and branch adequacy criteria were found to fail in satisfying several of the axioms including the applicability axiom. Some data flow adequacy criteria also failed to satisfy the applicability axiom. An additional three axioms/properties (shown here as 9-11) were added to the original set to provide an even stronger framework for evaluating test adequacy criteria. Weyuker meant for these axioms to be used as a tool by testers to understand the strengths and weaknesses of the criteria they select. Note that each criterion has a place on the Subsumes hierarchy as shown in Figure 5.5. A summary showing several criteria and eight of the axioms they satisfy, and fail to satisfy, is shown in Table 5.2.

Weyuker‘s goal for the research community is to eventually develop criteria that satisfy all of the axioms. Using these new criteria, testers will be able to have greater confidence that the code under test has been adequately tested. Until then testers will need to continue to use exiting criteria such as branch- and statement-based criteria. However, they should be aware of inherent weaknesses of each, and use combinations of criteria and different testing techniques to adequately test a program.