Chapter: Mathematics (maths) : Partial Differential Equations
Partial Differential Equations
PARTIAL DIFFERENTIAL EQUATIONS
This unit covers topics that explain the formation of partial differential equations and the solutions of special types of partial differential equations.
1 INTRODUCTION
2 FORMATION OF PARTIAL DIFFERNTIAL EQUATIONS
3 SOLUTIONS OF PARTIAL DIFFERENTIAL EQUATIONS
4 LAGRANGEŌĆÖS LINEAR EQUATIONS
5 PARTIAL DIFFERENTIAL EQUATIONS OF HIGHER ORDER WITH CONSTANT CO-EFFECIENTS
6 NON-HOMOGENOUS LINEAR EQUATIONS
1 INTRODUCTION
A partial differential equation is one which involves one or more partial derivatives. The order of the highest derivative is called the order of the equation. A partial differential equation contains more than one independent variable. But, here we shall consider partial differential only equation two independent variables x and y so that z = f(x,y). We shall denote
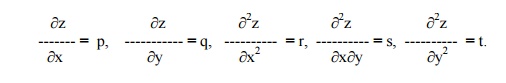
A partial differential equation is linear if it is of the first degree in the dependent variable and its partial derivatives. If each term of such an equation contains either the dependent variable or one of its derivatives, the equation is said to be homogeneous, otherwise it is non homogeneous.
2 Formation of Partial Differential Equations
Partial differential equations can be obtained by the elimination of arbitrary constants or by the elimination of arbitrary functions.
By the elimination of arbitrary constants
Let us consider the function
f( x, y, z, a, b ) = 0 ------------- (1)
where a & b are arbitrary constants
Differentiating equation (1) partially w.r.t x & y, we get
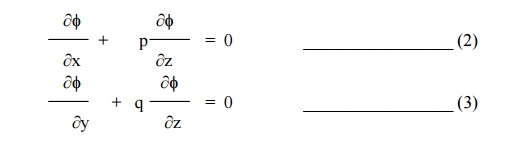
Eliminating a and b from equations (1), (2) and (3), we get a partial differential equation of the first order of the form f (x,y,z, p, q) = 0
Example 1
Eliminate the arbitrary constants a & b from z = ax + by + ab
Consider z = ax + by + ab ____________ (1)
Differentiating (1) partially w.r.t x & y, we get
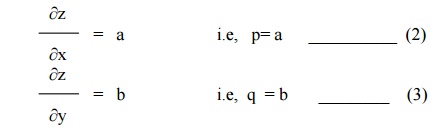
Using (2) & (3) in (1), we get
z = px +qy+ pq
which is the required partial differential equation.
Example 2
Form the partial differential equation by eliminating the arbitrary constants a and b from
z = ( x2 +a2 ) ( y2 + b 2)
Given z = ( x2 +a2 ) ( y2 + b2) ŌĆ”ŌĆ”..(1)
Differentiating (1) partially w.r.t x & y , we get
p = 2x (y2 + b2 )
q = 2y (x + a )
Substituting the values of p and q in (1), we get
4xyz = pq
which is the required partial differential equation.
Example 3
Find the partial differential equation of the family of spheres of radius one whose centre lie in the xy - plane.
The equation of the sphere is given by
( x ŌĆōa )2 + ( y- b) 2 + z2 = 1 _____________ (1)
Differentiating (1) partially w.r.t x & y , we get
2 (x-a ) + 2 zp = 0
2 ( y-b ) + 2 zq = 0
From these equations we obtain
x-a = -zp _________ (2)
y -b = -zq _________ (3)
Using (2) and (3) in (1), we get
z2p2 + z2q2 + z 2 = 1
or z2 ( p2 + q2 + 1) = 1
Example 4
Eliminate the arbitrary constants a, b & c from

and form the partial differential equation.
The given equation is

or -zp + xzr + p2x = 0
By the elimination of arbitrary functions
Let u and v be any two functions arbitrary function. This relation can be expressed as
u = f(v) ______________ (1)
Differentiating (1) partially w.r.t x & y and eliminating the arbitrary functions from these relations, we get a partial differential equation of the first order of the form
f(x, y, z, p, q ) = 0.
Example 5
Obtain the partial differential equation by eliminating ŌĆ×fŌĆ×from z = ( x+y ) f ( x2 - y2 )
Let us now consider the equation
z = (x+y ) f(x2- y2) _____________ (1)
Differentiating (1) partially w.r.t x & y , we get
p = ( x + y ) f ' ( x2 - y2 ) . 2x + f ( x2 - y2 )
q = ( x + y ) f ' ( x2 - y2 ) . (-2y) + f ( x2 - y2 )

i.e, py - yf( x2 - y2 ) = -qx +xf ( x2 - y2 )
i.e, py +qx = ( x+y ) f ( x2 - y2 )
Therefore, we have by(1), py +qx = z
Example 6
Form the partial differential equation by eliminating the arbitrary function f
from
z = ey f (x + y)
Consider z = ey f ( x +y ) ___________ ( 1)
Differentiating (1) partially w .r. t x & y, we get
p = ey f ' (x + y)
q = ey f '(x + y) + f(x + y). ey
Hence, we have
q = p + z
Example 7

Exercises:
1. 1. Form the partial differential equation by eliminating the arbitrary constants ŌĆ×aŌƤ & ŌĆ×bŌƤ from the following equations.
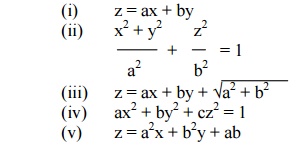
2. Find the PDE of the family of spheres of radius 1 having their centres lie on the xy plane{Hint: (x ŌĆōa)2 + (y ŌĆōb)2 + z2 = 1}
3. Find the PDE of all spheres whose centre lie on the (i) z axis (ii) x-axis
4. Form the partial differential equations by eliminating the arbitrary functions in the following cases.
(i) z = f (x + y)
(ii) z = f (x2 ŌĆōy2)
(iii) z = f (x2 + y2 + z2)
(iv) f(xyz, x + y + z) = 0
(v) F (xy + z2, x + y + z) = 0
(vi) z = f (x + iy) +f (x ŌĆōiy)
(vii) z = f(x3 + 2y) +g(x3 ŌĆō2y)
3 SOLUTIONS OF A PARTIAL DIFFERENTIAL EQUATION
A solution or integral of a partial differential equation is a relation connecting the dependent and the independent variables which satisfies the given differential equation. A partial differential equation can result both from elimination of arbitrary constants and from elimination of arbitrary functions as explained in section 1.2. But, there is a basic difference in the two forms of solutions. A solution containing as many arbitrary constants as there are independent variables is called a complete integral. Here, the partial differential equations contain only two independent variables so that the complete integral will include two constants.A solution obtained by giving particular values to the arbitrary constants in a complete integral is called a particular integral.
Singular Integral
Let f (x,y,z,p,q) = 0 ---------- (1)
be the partial differential equation whose complete integral is
f (x,y,z,a,b) = 0----------- (2)
where ŌĆ×aŌƤ and ŌĆ×bŌƤ are arbitrary constants.
Differentiating (2) partially w.r.t. a and b, we obtain

The eliminant of ŌĆ×aŌƤ and ŌĆ×bŌƤ from the equations (2), (3) and (4), when it exists, is called the singular integral of (1).
General Integral
In the complete integral (2), put b = F(a), we get
f (x,y,z,a, F(a) ) = 0 ---------- (5)
Differentiating (2), partially w.r.t.a, we get

The eliminant of ŌĆ×aŌƤ between (5) and (6), if it exists, is called the general integral of (1).
SOLUTION OF STANDARD TYPES OF FIRST ORDER PARTIAL
DIFFERENTIAL EQUATIONS.
The first order partial differential equation can be written as
f(x,y,z, p,q) = 0,
where p = ┬Čz/┬Čx and q = ┬Čz / ┬Čy. In this section, we shall solve some standard forms of equations by special methods.
Standard I : f (p,q) = 0. i.e, equations containing p and q only.
Suppose that z = ax + by +c is a solution of the equation f(p,q) = 0, where f (a,b)
= 0.
Solving this for b, we get b = F (a).
Hence the complete integral is z = ax + F(a) y +c------------ | (1) |
Now, the singular integral is obtained by eliminating a & c between
z = ax + y F(a) + c 0 = x + y F'(a)
0 = 1.
The last equation being absurd, the singular integral does not exist in this case.
To obtain the general integral, let us take c = F (a).
Then, z = ax + F(a) y + F (a) -------------- (2)
Differentiating (2) partially w.r.t. a, we get
0 = x + F'(a). y + F '(a) --------------- (3)
EliminatingŌƤbetweenŌĆ×a (2) and (3), we get the gene
Example 8
Solve pq = 2
The given equation is of the form f (p,q) = 0
The solution is z = ax + by +c, where ab = 2.
Solving, b = 2/b
The complete integral is
Z = ax + 2/a y + c ---------- (1)
Differentiating (1) partially w.r.t ŌĆ×cŌƤ, we
0 = 1,
which is absurd. Hence, there is no singular integral.
To find the general integral, put c = ’üå (a) in (1), we get
Z = ax + 2/a y + F (a)
Differentiating partially w.r.t ŌĆ×aŌƤ, we get
0 = x ŌĆō 2/ a2 y + F ŌĆś(a)
Eliminating ŌĆ×aŌƤ between these equations gives the general integral.
Example 9
Solve pq + p +q = 0
The given equation is of the form f (p,q) = 0.
The solution is z = ax + by +c, where ab + a + b = 0.
Solving, we get
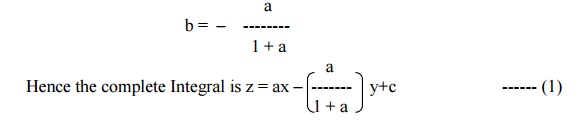
Differentiating (1) partially w.r.t. ŌĆ×cŌƤ, we get
0 = 1.
The above equation being absurd, there is no singular integral for the given partial differential equation.
To find the general integral, put c = F (a) in (1), we have
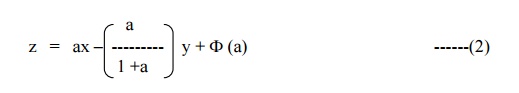
Differentiating (2) partially w.r.t a, we get
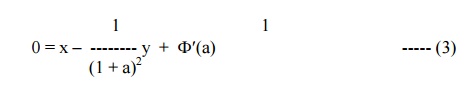
Example 10
Solve p2 + q2 = npq
The solution of this equation is z = ax + by + c, where a2 + b2 = nab.
Solving, we get

Differentiating (1) partially w.r.t c, we get 0 = 1, which is absurd. Therefore, there is no singular integral for the given equation.
To find the general Integral, put C = F (a), we get

The eliminant of ŌĆ×aŌƤ between these equations gives the general integral
Standard II : Equations of the form f (x,p,q) = 0, f (y,p,q) = 0 and f (z,p,q) = 0. i.e, one of the variables x,y,z occurs explicitly.
(i) Let us consider the equation f (x,p,q) = 0.
Since z is a function of x and y, we have
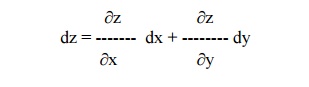
or dz = pdx + qdy
Assume that q = a.
Then the given equation takes the form f (x, p,a ) = 0
Solving, we get p = F(x,a).
Therefore, dz = F(x,a) dx + a dy.
(ii) Let us consider the equation f(y,p,q) = 0. Assume that p = a.
Then the equation becomes f (y,a, q) = 0 Solving, we get q = F (y,a).
Therefore, dz = adx + F(y,a) dy.
Integrating, z = ax + ├▓F(y,a) dy + b, which is a complete Integral.
(iii) Let us consider the equation f(z, p, q) = 0.
Assume that q = ap.
Then the equation becomes f (z, p, ap) = 0
Solving, we get p = F(z,a). Hence dz = F(z,a) dx + a F(z, a) dy.
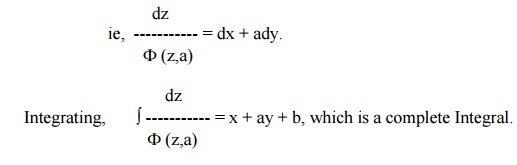
Example 11
Solve q = xp + p2
Given q = xp + p2 -------------(1)
This is of the form f (x,p,q) = 0.
Put q = a in (1), we get
a = xp + p2
i.e, p2 + xp ŌĆōa = 0.
Therefore,
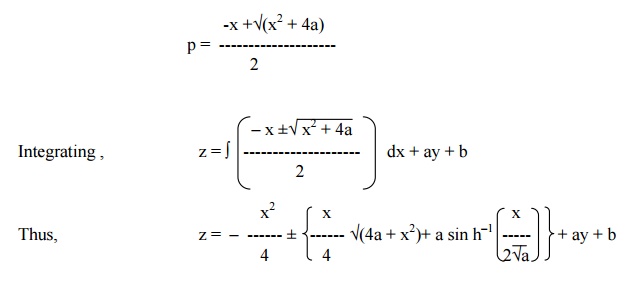
Example 12
Solve q = yp2
This is of the form f (y,p,q) = 0
Then, put p = a.
Therfore, the given equation becomes q = a2y.
Since dz = pdx + qdy, we have
dz = adx + a2y dy
Integrating, we get z = ax + (a2y2/2) + b
Example 13
Solve 9 (p2z + q2) = 4
This is of the form f (z,p,q) = 0
Then, putting q = ap, the given equation becomes
9 (p2z + a2p2) = 4

or (z + a2)3/2 = x + ay + b.
Standard III : f1(x,p) = f2 (y,q). ie, equations in which ŌĆśzŌĆÖ is absent and the variables are separable.
Let us assume as a trivial solution that
f(x,p) = g(y,q) = a (say).
Solving for p and q, we get p = F(x,a) and q = G(y,a).
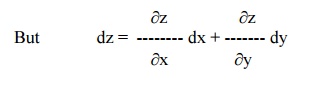
Hence dz = pdx + qdy = F(x,a) dx + G(y,a) dy
Therefore, z = ├▓F(x,a) dx + ├▓G(y,a) dy + b , which is the complete integral of the given equation containing two constants a and b. The singular and general integrals are found in the usual way.
Example 14
Solve pq = xy
The given equation can be written as

Example 15
Solve p2 + q2 = x2 + y2
The given equation can be written as p2 ŌĆōx2 = y2 ŌĆōq2 = a2 (say)
p2 ŌĆōx2 = a2 Implies p = ├¢(a2 + x2)
andy2 ŌĆōq2 = a2 Implies q = ├¢(y2 ŌĆōa2)
But dz = pdx + qdy
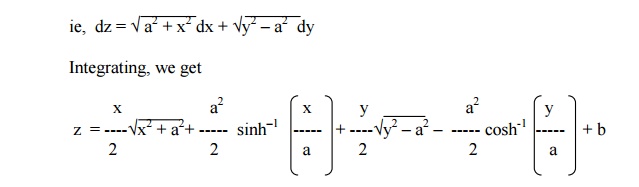
Standard IV (ClairautŌĆÖs) form
Equation of the type z = px + qy + f (p,q) ------(1) is known as ClairautŌƤs
Differentiating (1) partially w.r.t x and y, we get p = a and q = b.
Therefore, the complete integral is given by
z = ax + by + f (a,b).
Example 16
Solve z = px + qy +pq
The given equation is in ClairautŌƤs. form
Putting p = a and q = b, we have
z = ax + by + ab -------- (1)
which is the complete integral.
To find the singular integral, differentiating (1) partially w.r.t a and b, we get
0 = x + b
0 = y + a
Therefore we have, a = -y and b= -x.
Substituting the values of a & b in (1), we get
z = -xy ŌĆōxy + xy
or z + xy = 0, which is the singular integral.
To get the general integral, put b = F(a) in (1).
Then z = ax + F(a)y + a F(a) ---------- (2)
Differentiating (2) partially w.r.t a, we have
0 = x + F'(a) y + aF'(a) + F(a) ---------- (3)
Eliminating ŌĆ×aŌƤ between (2) and (3), we get the general integral.
Example 17
Find the complete and singular solutions of


Exercises
Solve the following Equations
1. pq = k
2. p + q = pq
3. Ûp +Ûq = x
4. p = y2q2
5. z = p2 + q2
6. p + q = x + y
7. p2z2 + q2 = 1
8. z = px + qy - 2Ûpq
9. {z ŌĆō(px + qy)}2 = c2 + p2 + q2
10. z = px + qy + p2q2
EQUATIONS REDUCIBLE TO THE STANDARD FORMS
Sometimes, it is possible to have non ŌĆōlinear partial differential equations of the first order which do not belong to any of the four standard forms discussed earlier. By changing the variables suitably, we will reduce them into any one of the four standard forms.
Type (i) : Equations of the form F(xm p, ynq) = 0 (or) F (z, xmp, ynq) = 0.
Case(i) : If m ┬╣1 and n ┬╣1, then put x1-m = X and y1-n = Y.
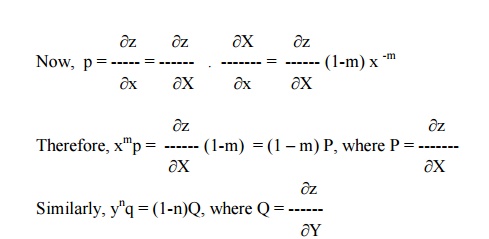
Hence, the given equation takes the form F(P,Q) = 0 (or) F(z,P,Q) = 0.
Case(ii) : If m = 1 and n = 1, then put log x = X and log y = Y.
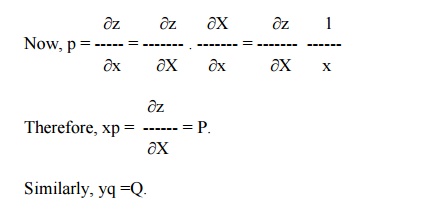
Example 18
Solve x4p2 + y2zq = 2z2
The given equation can be expressed as
(x2p)2 + (y2q)z = 2z2
Here m = 2, n = 2
Put X = x1-m = x -1 and Y = y 1-n = y -1.
We have xmp = (1-m) P and ynq = (1-n)Q
i.e, x2p = -P and y2q = -Q.
Hence the given equation becomes
P2 ŌĆōQz = 2z2 ----------(1)
This equation is of the form f (z,P,Q) = 0.
Let us take Q = aP.
Then equation (1) reduces to
P2 ŌĆōaPz =2z2
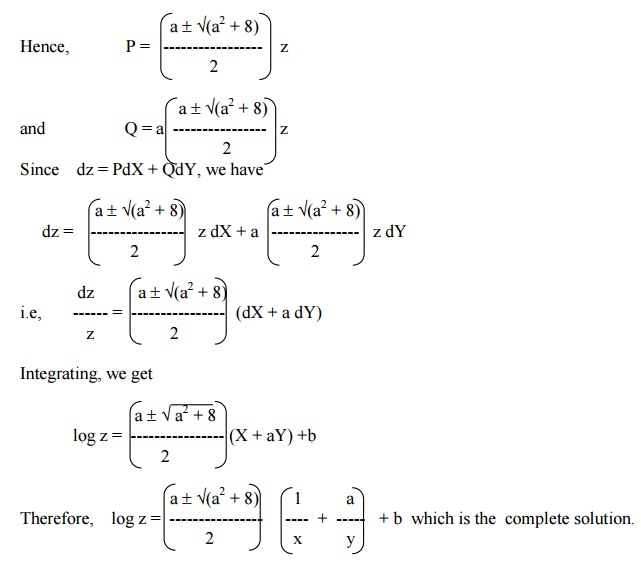
Example 19
Solve x2p2 + y2q2 = z2
The given equation can be written as
(xp)2 + (yq)2 = z2
Here m = 1, n = 1.
Put X = log x and Y = log y.
Then xp = P and yq = Q.
Hence the given equation becomes
P2 + Q2 = z2 ------------- (1)
This equation is of the form F(z,P,Q) = 0.
Therefore, let us assume that Q = aP.
Now, equation (1) becomes,
P2 + a2 P2 = z2

Integrating, we get
Û(1+a2) log z = X + aY + b.
Therefore, Û(1+a2) log z = logx + alogy + b, which is the complete solution.
Type (ii) : Equations of the form F(zkp, zkq) = 0 (or) F(x, zkp) = G(y,zkq).
Case (i) : If k ┬╣-1, put Z = zk+1,

Example 20
Solve z4q2 ŌĆōz2p = 1
The given equation can also be written as
(z2q)2 ŌĆō(z2p) =1
Here k = 2. Putting Z = z k+1 = z3, we get
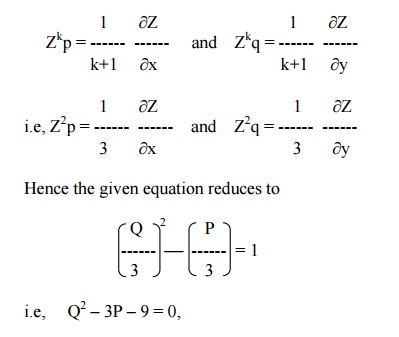
i.e, Q2 ŌĆō3P ŌĆō9 = 0,
which is of the form F(P,Q) = 0.
Hence its solution is Z = ax + by + c, where b2 ŌĆō3a ŌĆō9 = 0.
Solving for b, b = ± Û(3a +9)
Hence the complete solution is
Z = ax + Û(3a +9) . y + c
or z3 = ax + Û(3a +9) y + c

4 LagrangeŌĆÖs Linear Equation
Equations of the form Pp + Qq = R ________ (1), where P, Q and R are functions of x, y, z, are known as Lagrang solve this equation, let us consider the equations u = a and v = b, where a, b are arbitrary constants and u, v are functions of x, y, z.

Equations (5) represent a pair of simultaneous equations which are of the first order and of first degree.Therefore, the two solutions of (5) are u = a and v = b. Thus, f( u, v ) = 0 is the required solution of (1).
Note :
To solve the LagrangeŌƤs equation,we have to form the subsidiary or auxiliary equations
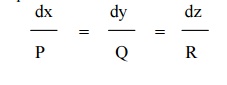
which can be solved either by the method of grouping or by the method of multipliers.
Example 21
Find the general solution of px + qy = z.
Here, the subsidiary equations are
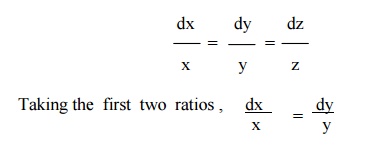
Integrating, log x = log y + log c1
or x = c1 y i.e, c1 = x / y
From the last two ratios,
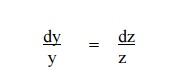
Integrating, log y = log z + log c2
or y = c2 z
i.e, c2 = y / z
Hence the required general solution is
╬”( x/y,= 0,y/z)where ╬” is arbitrary
Example 22
Solve p tan x + q tan y = tan z
The subsidiary equations are
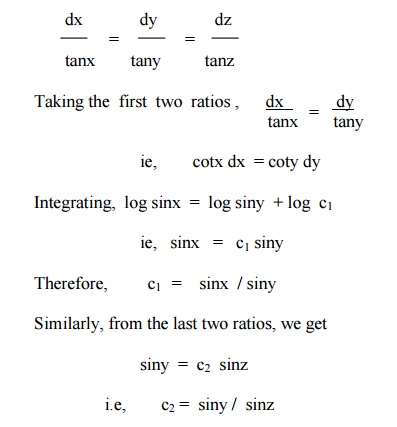
Hence the required general solution is
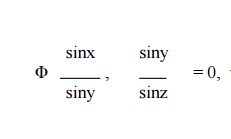
where ╬” is arbitrary
Example 23
Solve (y-z) p + (z-x) q = x-y
Here the subsidiary equations are

Example 24
Find the general solution of (mz - ny) p + (nx- lz)q = ly - mx.

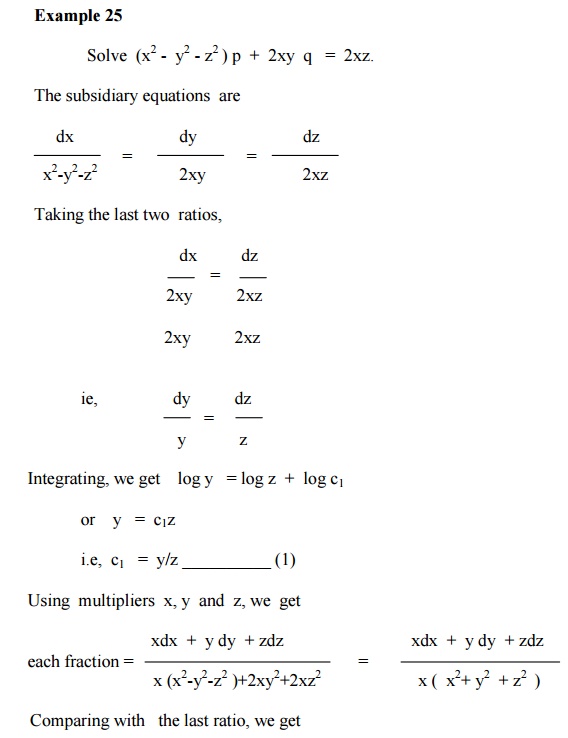

Exercises
Solve the following equations
1. px2 + qy2 = z2
2. pyz + qzx = xy
3. xp ŌĆōyq = y2 ŌĆōx2
4. y2zp + x2zq = y2x
5. z (x ŌĆōy) = px2 ŌĆōqy2
6. (a ŌĆōx) p + (b ŌĆōy) q = c ŌĆōz
7. (y2z p) /x + xzq = y2
8. (y2 + z2) p ŌĆōxyq + xz = 0
9. x2p + y2q = (x + y) z
10. p ŌĆōq = log (x+y)
11. (xz + yz)p + (xz ŌĆōyz)q = x2 + y2
12. (y ŌĆōz)p ŌĆō(2x + y)q = 2x + z
5 PARTIAL DIFFERENTIAL EQUATIONS OF HIGHER ORDER WITH CONSTANT COEFFICIENTS.
Homogeneous Linear Equations with constant Coefficients.
A homogeneous linear partial differential equation of the nth order is of the form
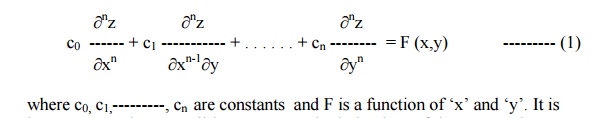
homogeneous because all its terms contain derivatives of the same order.
Equation (1) can be expressed as
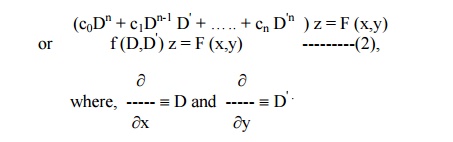
As in the case of ordinary linear equations with constant coefficients the complete solution of (1) consists of two parts, namely, the complementary function and the particular integral.
The complementary function is the complete solution of f (D,D') z = 0-------(3), which must contain n arbitrary functions as the degree of the polynomial f(D,D'). The particular integral is the particular solution of equation (2).
Finding the complementary function
Let us now consider the equation f(D,D') z = F (x,y)
The auxiliary equation of (3) is obtained by replacing D by m and D' by 1.
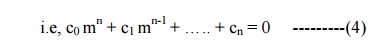
Solving equation (4) for ŌĆ×mŌƤ, we get ŌĆ×nŌƤ roots. Depending upon the nature of the roots, the Complementary function is written as given below:

Finding the particular Integral

Expand [f (D,D')]-1 in ascending powers of D or D' and operate on xm yn term by term.
Case (iv) : When F(x,y) is any function of x and y.

into partial fractions considering f (D,D') as a function of D alone.
Then operate each partial fraction on F(x,y) in such a way that
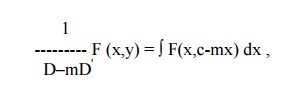
where c is replaced by y+mx after integration
Example 26
Solve(D3 ŌĆō3D2D' + 4D'3) z = ex+2y
The auxillary equation is m=m3 ŌĆō3m2 + 4 = 0
The roots are m = -1,2,2
Therefore the C.F is f1(y-x) + f2 (y+ 2x) + xf3 (y+2x).

Hence, the solution is z = C.F. + P.I
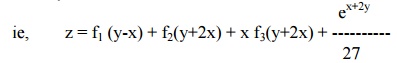
Example 27
Solve (D2 ŌĆō4DD' +4 D' 2) z = cos (x ŌĆō2y)
The auxiliary equation is m2 ŌĆō4m + 4 = 0
Solving, we get m = 2,2.
Therefore the C.F is f1(y+2x) + xf2(y+2x).
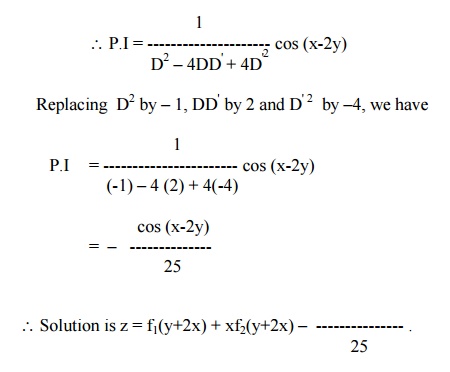
Example 28
Solve (D2 ŌĆō2DD') z = x3y + e5x
The auxiliary equation is m2 ŌĆō2m = 0.
Solving, we get m = 0,2.
Hence the C.F is f1 (y) + f2 (y+2x).
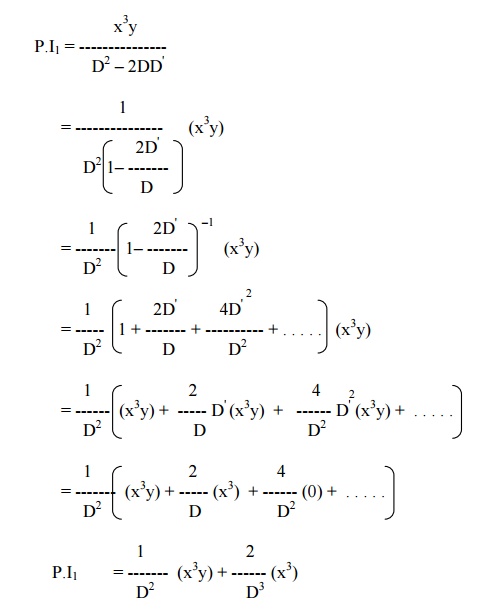
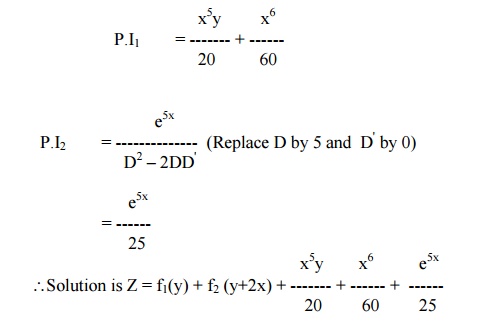
Example 29
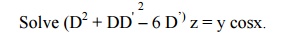
The auxiliary equation is m2 + m ŌĆō6 = 0.
Therefore, m = ŌĆō3, 2.
Hence the C.F is f1(y-3x) + f2(y + 2x).
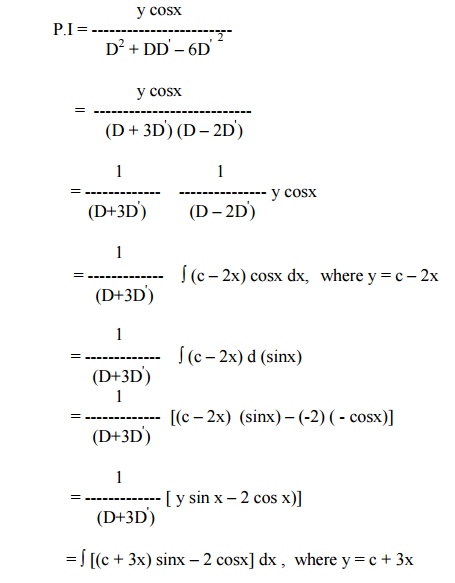
= ├▓(c + 3x) d(ŌĆōcosx) ŌĆō2├▓cosx dx
= (c + 3x) (ŌĆōcosx) ŌĆō(3) ( - sinx) ŌĆō2 sinx
= ŌĆōy cosx + sinx
Hence the complete solution is
z = f1(y ŌĆō3x) + f2(y + 2x) ŌĆōy cosx + sinx
Example 30
Solve r ŌĆō4s + 4t = e 2x +y
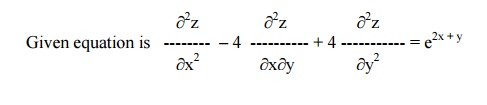
i.e, (D2 ŌĆō4DD' + 4D' 2 ) z = e2x + y
The auxiliary equation is m2 ŌĆō4m + 4 = 0.
Therefore, m = 2,2
Hence the C.F is f1(y + 2x) + x f2(y + 2x).
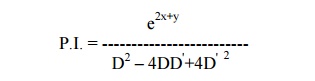
Since D2 ŌĆō4DD'+4D'2 = 0 for D = 2 and D' = 1, we have to apply the general rule.
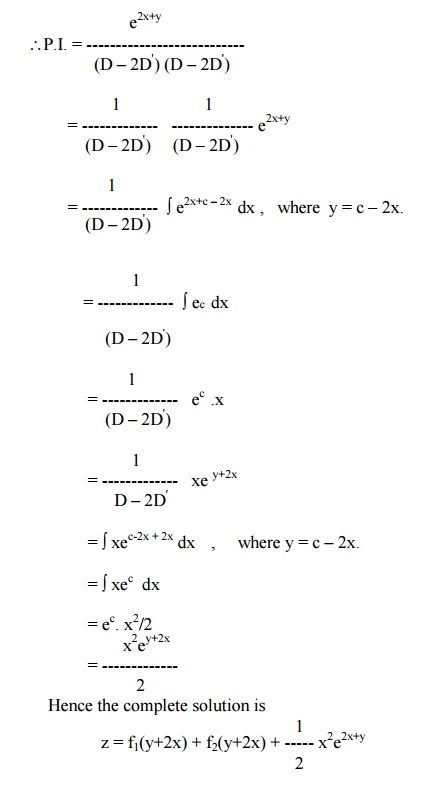
6 Non ŌĆōHomogeneous Linear Equations
Let us consider the partial differential equation
f (D,D') z = F (x,y)------- (1)
If f (D,D') is not homogeneous, then (1) is a nonŌĆōhomogeneous linear partial differential equation. Here also, the complete solution = C.F + P.I.
The methods for finding the Particular Integrals are the same as those for homogeneous linear equations.
But for finding the C.F, we have to factorize f (D,D') into factors of the form D ŌĆōmD' ŌĆōc.
Consider now the equation
(D ŌĆōmD' ŌĆōc) z = 0 ----------- (2).
This equation can be expressed as
p ŌĆōmq = cz ---------(3),
which is in Lagrangian form.
The subsidiary equations are
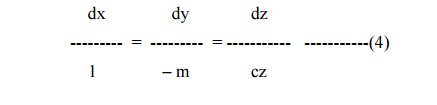
The solutions of (4) are y + mx = a and z = becx.
Taking b = f (a), we get z = ecx f (y+mx) as the solution of (2).
Note:
1. If (D-m1D' ŌĆōC1) (D ŌĆōm2D'-C2) ŌĆ”ŌĆ” ŌĆōm(Dn'-Cn) z = 0 is the partial
differential equation, then its complete solution is
z = ec1x f1(y +m1x) + ec2x f2(y+m2x) + . . . . . + ecnx fn(y+mnx)
2. In the case of repeated factors, the equation (D-mD' ŌĆōC)nz = 0 has a complete
solution z = ecx f1(y +mx) + x ecx f2(y+mx) + . . . . . +x n-1 ecx fn(y+mx).
Example 31
Solve (D-D'-1) (D-D' ŌĆō2)z = e 2x ŌĆōy
Here m1 = 1, m2 = 1, c1 = 1, c2 = 2.
Therefore, the C.F is ex f1 (y+x) + e2x f2 (y+x).

Example 32
Solve (D2 ŌĆōDD' + D' ŌĆō1) z = cos (x + 2y)
The given equation can be rewritten as
(D-D'+1) (D-1) z = cos (x + 2y)
Here m1 = 1, m2 = 0, c1 = -1, c2 = 1.
Therefore, the C.F = eŌĆōx f1(y+x) + ex f2 (y)
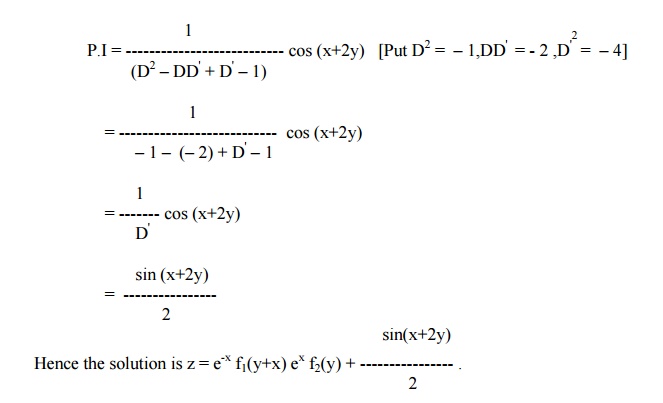
Example 33
Solve [(D + D'ŌĆō1) (D + 2D' ŌĆō3)] z = ex+2y + 4 + 3x +6y
Here m1 = ŌĆō1, m2 = ŌĆō2 , c1 = 1, c2 = 3.
Hence the C.F is z = ex f1(y ŌĆōx) + e3x f2(y ŌĆō2x).


It is the complete solution.
Exercises
(a) Solve the following homogeneous Equations.
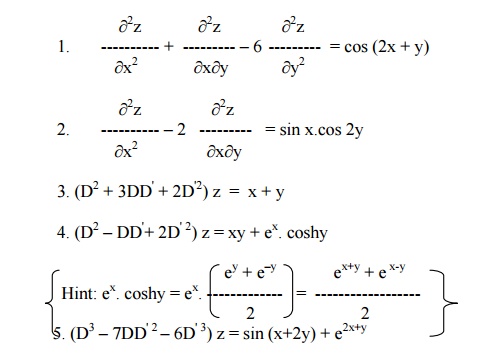
6. (D2 + 4DD' ŌĆō5D'2) z = 3e2x-y + sin (x ŌĆō2y)
7. (D2 ŌĆōDD' ŌĆō30D'2) z = xy + e6x+y
8. (D2 ŌĆō4D' 2) z = cos2x. cos3y
9. (D2 ŌĆōDD' ŌĆō2D'2) z = (y ŌĆō1)ex
10.4r + 12s + 9t = e3x ŌĆō2y
(b)Solve the following non ŌĆōhomogeneous equations.
1. (2DD' + D' 2 ŌĆō3D') z = 3 cos(3x ŌĆō2y)
2. (D2 + DD' + D' ŌĆō1) z = e-x
3. r ŌĆōs + p = x2 + y2
4. (D2 ŌĆō2DD' + D'2 ŌĆō3D + 3D' + 2)z = (e3x + 2e-2y)2
(D2 ŌĆōD'2 ŌĆō3D + 3D') z = xy + 7.
Related Topics