Chapter: Mathematics (maths) : Partial Differential Equations
Partial Differential Equations of Higher Order With Constant Coefficients
PARTIAL DIFFERENTIAL EQUATIONS OF HIGHER ORDER WITH CONSTANT COEFFICIENTS.
Homogeneous Linear Equations with constant Coefficients.
A homogeneous linear partial differential equation of the nth order is of the form
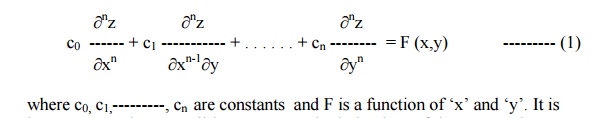
homogeneous because all its terms contain derivatives of the same order.
Equation (1) can be expressed as
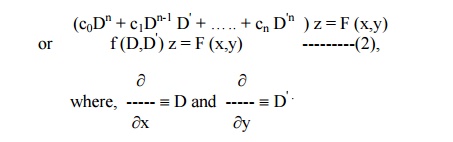
As in the case of ordinary linear equations with constant coefficients the complete solution of (1) consists of two parts, namely, the complementary function and the particular integral.
The complementary function is the complete solution of f (D,D') z = 0-------(3), which must contain n arbitrary functions as the degree of the polynomial f(D,D'). The particular integral is the particular solution of equation (2).
Finding the complementary function
Let us now consider the equation f(D,D') z = F (x,y)
The auxiliary equation of (3) is obtained by replacing D by m and D' by 1.
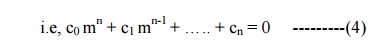
Solving equation (4) for „m‟, we get „n‟ roots. Depending upon the nature of the roots, the Complementary function is written as given below:

Finding the particular Integral

Expand [f (D,D')]-1 in ascending powers of D or D' and operate on xm yn term by term.
Case (iv) : When F(x,y) is any function of x and y.

into partial fractions considering f (D,D') as a function of D alone.
Then operate each partial fraction on F(x,y) in such a way that
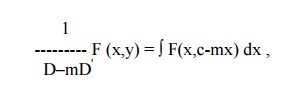
where c is replaced by y+mx after integration
Example 26
Solve(D3 –3D2D' + 4D'3) z = ex+2y
The auxillary equation is m=m3 –3m2 + 4 = 0
The roots are m = -1,2,2
Therefore the C.F is f1(y-x) + f2 (y+ 2x) + xf3 (y+2x).

Hence, the solution is z = C.F. + P.I
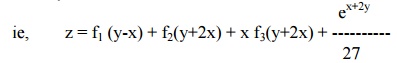
Example 27
Solve (D2 –4DD' +4 D' 2) z = cos (x –2y)
The auxiliary equation is m2 –4m + 4 = 0
Solving, we get m = 2,2.
Therefore the C.F is f1(y+2x) + xf2(y+2x).
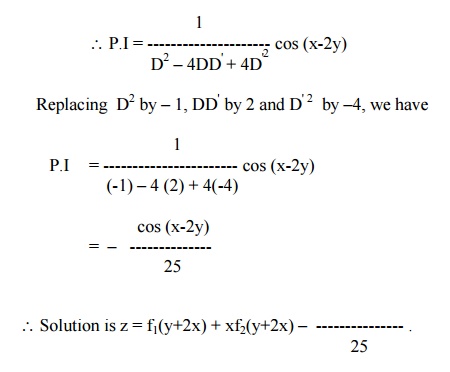
Example 28
Solve (D2 –2DD') z = x3y + e5x
The auxiliary equation is m2 –2m = 0.
Solving, we get m = 0,2.
Hence the C.F is f1 (y) + f2 (y+2x).
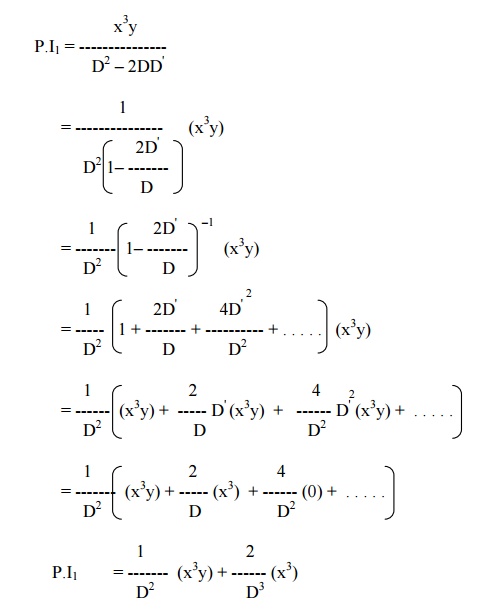
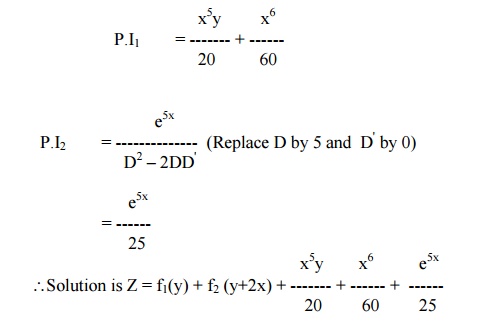
Example 29
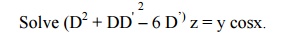
The auxiliary equation is m2 + m –6 = 0.
Therefore, m = –3, 2.
Hence the C.F is f1(y-3x) + f2(y + 2x).
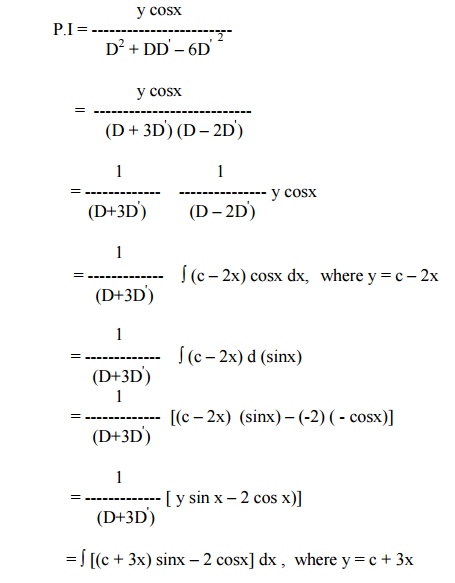
= ò(c + 3x) d(–cosx) –2òcosx dx
= (c + 3x) (–cosx) –(3) ( - sinx) –2 sinx
= –y cosx + sinx
Hence the complete solution is
z = f1(y –3x) + f2(y + 2x) –y cosx + sinx
Example 30
Solve r –4s + 4t = e 2x +y
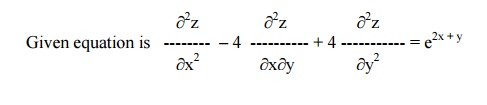
i.e, (D2 –4DD' + 4D' 2 ) z = e2x + y
The auxiliary equation is m2 –4m + 4 = 0.
Therefore, m = 2,2
Hence the C.F is f1(y + 2x) + x f2(y + 2x).
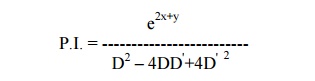
Since D2 –4DD'+4D'2 = 0 for D = 2 and D' = 1, we have to apply the general rule.
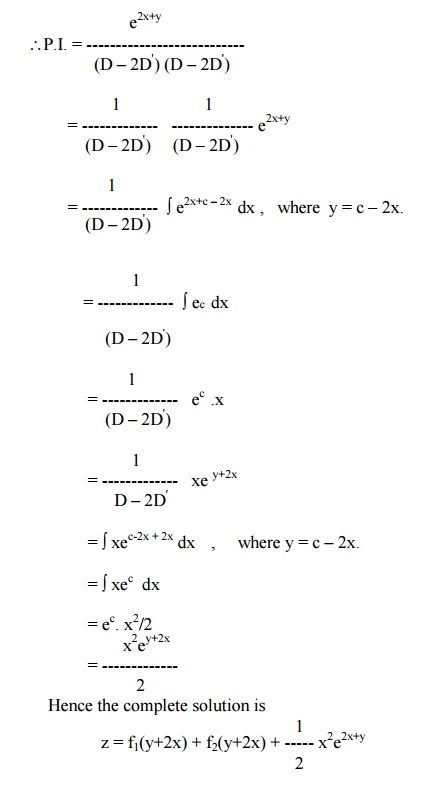
Related Topics