Chapter: Mathematics (maths) : Partial Differential Equations
Non Homogeneous Linear Equations
Non –Homogeneous Linear Equations
Let us consider the partial differential equation
f (D,D') z = F (x,y)------- (1)
If f (D,D') is not homogeneous, then (1) is a non–homogeneous linear partial differential equation. Here also, the complete solution = C.F + P.I.
The methods for finding the Particular Integrals are the same as those for homogeneous linear equations.
But for finding the C.F, we have to factorize f (D,D') into factors of the form D –mD' –c.
Consider now the equation
(D –mD' –c) z = 0 ----------- (2).
This equation can be expressed as
p –mq = cz ---------(3),
which is in Lagrangian form.
The subsidiary equations are
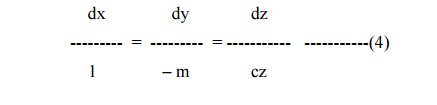
The solutions of (4) are y + mx = a and z = becx.
Taking b = f (a), we get z = ecx f (y+mx) as the solution of (2).
Note:
1. If (D-m1D' –C1) (D –m2D'-C2) …… –m(Dn'-Cn) z = 0 is the partial
differential equation, then its complete solution is
z = ec1x f1(y +m1x) + ec2x f2(y+m2x) + . . . . . + ecnx fn(y+mnx)
2. In the case of repeated factors, the equation (D-mD' –C)nz = 0 has a complete
solution z = ecx f1(y +mx) + x ecx f2(y+mx) + . . . . . +x n-1 ecx fn(y+mx).
Example 31
Solve (D-D'-1) (D-D' –2)z = e 2x –y
Here m1 = 1, m2 = 1, c1 = 1, c2 = 2.
Therefore, the C.F is ex f1 (y+x) + e2x f2 (y+x).

Example 32
Solve (D2 –DD' + D' –1) z = cos (x + 2y)
The given equation can be rewritten as
(D-D'+1) (D-1) z = cos (x + 2y)
Here m1 = 1, m2 = 0, c1 = -1, c2 = 1.
Therefore, the C.F = e–x f1(y+x) + ex f2 (y)
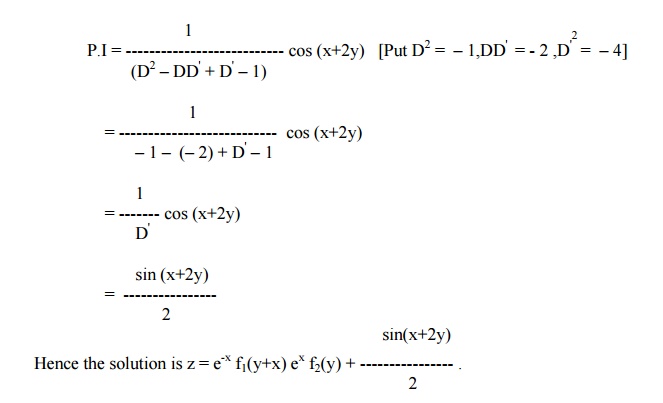
Example 33
Solve [(D + D'–1) (D + 2D' –3)] z = ex+2y + 4 + 3x +6y
Here m1 = –1, m2 = –2 , c1 = 1, c2 = 3.
Hence the C.F is z = ex f1(y –x) + e3x f2(y –2x).


It is the complete solution.
Exercises
(a) Solve the following homogeneous Equations.
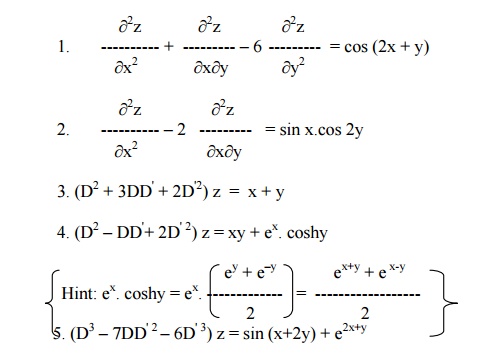
6. (D2 + 4DD' –5D'2) z = 3e2x-y + sin (x –2y)
7. (D2 –DD' –30D'2) z = xy + e6x+y
8. (D2 –4D' 2) z = cos2x. cos3y
9. (D2 –DD' –2D'2) z = (y –1)ex
10.4r + 12s + 9t = e3x –2y
(b)Solve the following non –homogeneous equations.
1. (2DD' + D' 2 –3D') z = 3 cos(3x –2y)
2. (D2 + DD' + D' –1) z = e-x
3. r –s + p = x2 + y2
4. (D2 –2DD' + D'2 –3D + 3D' + 2)z = (e3x + 2e-2y)2
(D2 –D'2 –3D + 3D') z = xy + 7.
Related Topics