Chapter: Mathematics (maths) : Fourier Series
Fourier Series
FOURIER SERIES
1 INTRODUCTION
2 PERIODIC FUNCTIONS
3 EVEN AND ODD FUNCTIONS
4 HALF RANGE SERIES
5 PARSEVAL’S THEOREM
6 CHANGE OF INTERVAL
7 HARMONIC ANALYSIS
8 COMPLEX FORM OF FOURIER SERIES
9 SUMMARY
1 INTRODUCTION
The concept of Fourier series was first introduced by Jacques Fourier (1768– 1830), French Physicist and Mathematician. These series became a most important tool in Mathematical physics and had deep influence on the further development of mathematics it self.Fourier series are series of cosines and sines and arise in representing general periodic functions that occurs in many Science and Engineering problems. Since the periodic functions are often complicated, it is necessary to express these in terms of the simple periodic functions of sine and cosine. They play an important role in solving ordinary and partial differential equations.
2 PERIODIC FUNCTIONS
A function f (x) is called periodic if it is defined for all real „x‟ some positive number „p‟ such that
f (x + p ) = f (x) for all x.
This number „p‟ is called a period of f(x
If a periodic function f (x) has a smallest period p (>0), this is often called the fundamental period of f(x). For example, the functions cosx and sinx have fundamental period 2p.
DIRICHLET CONDITIONS
Any function f(x), defined in the interval c £x £c + 2p, can be developed as a Fourier series of the form
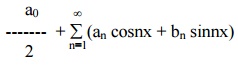
provided the following conditions are satisfied.
f (x) is periodic, single–valued and finite in [ c, c + 2 p].
f (x) has a finite number of discontinuities in [ c, c + 2p].
f (x) has at the most a finite number of maxima and minima in [ c,c+ 2p].
These conditions are known as Dirichlet conditions. When these conditions are satisfied, the Fourier series converges to f(x) at every point of continuity. At a point of discontinuity x = c, the sum of the series is given by
f(x) = (1/2) [ f (c-0) + f (c+0)] ,
where f (c-0) is the limit on the left and f (c+0) is the limit on the right.
EULER’S FORMULAE
The Fourier series for the function f(x) in the interval c < x < c + 2pis given by
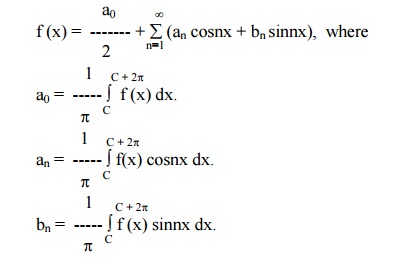
These values of a0, an, bn are known as Euler‟s 0 , formula en,bn The coefficients a0, an, bn are are also termed as Fourier coefficients.
Example 1
Expand f(x) = x as Fourier Series (Fs) in the interval [ -π, π]
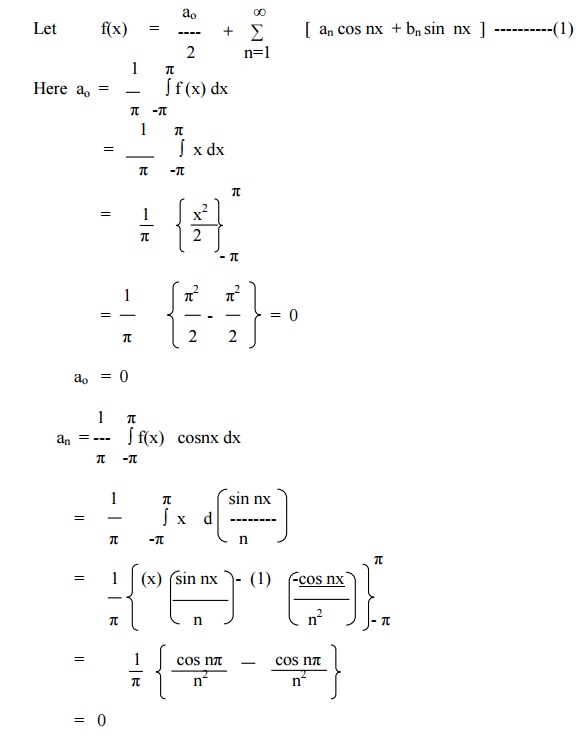
Example 2
Expand f(x) = x2 in the interval ( -p£x £p) and hence deduce that
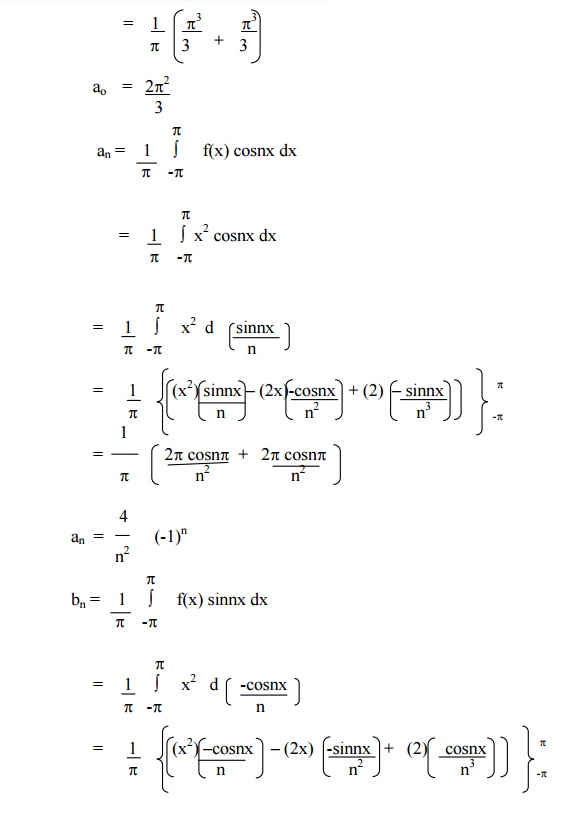
Example 3
Obtain the Fourier Series of periodicity 2πin [for-π, π]
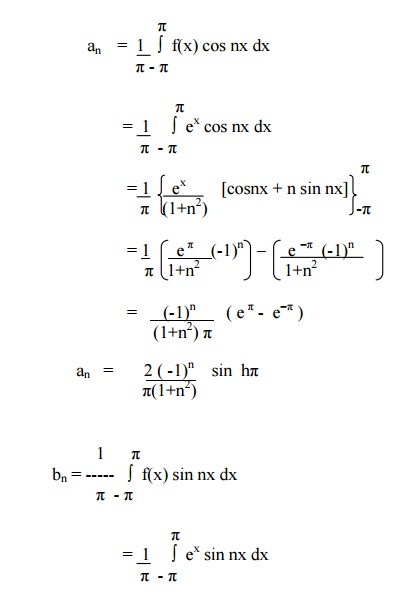
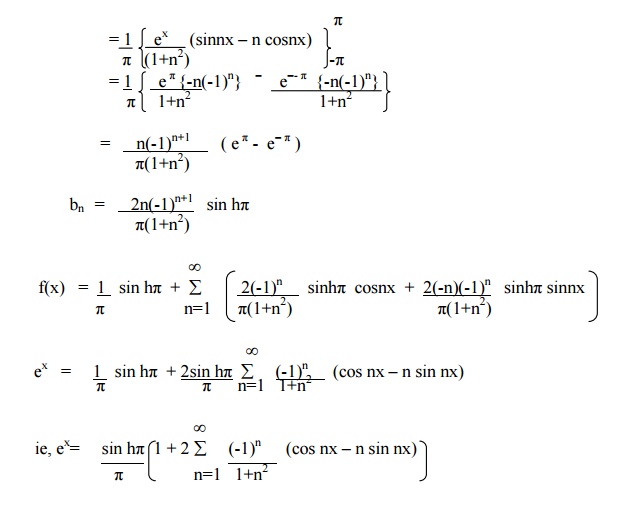
Example 4
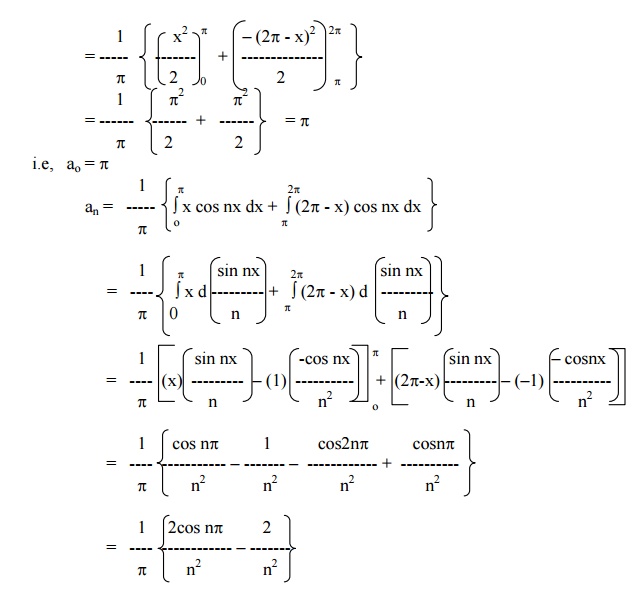
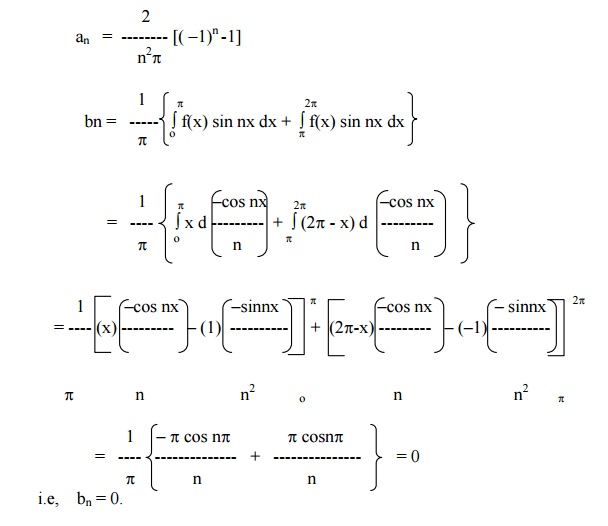
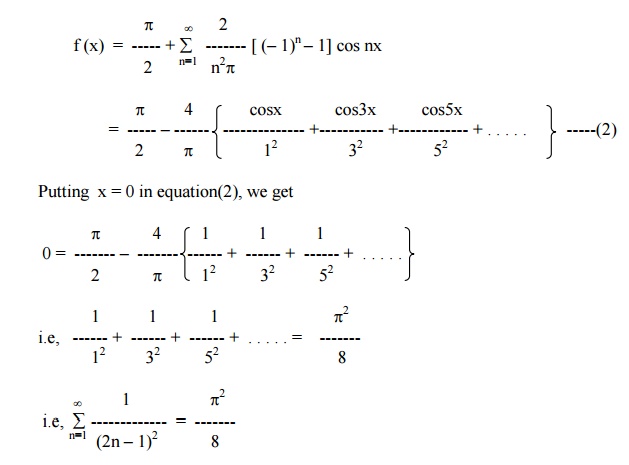
Example 5
Find the Fourier series for f (x) = (x + x2) in (-p< x < p) of percodicity 2p and hence deduce that
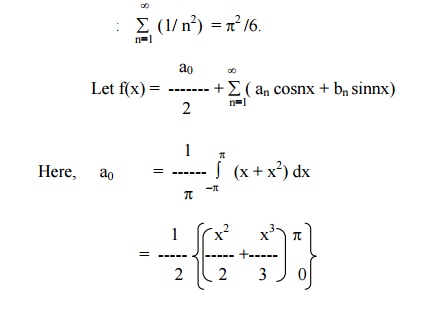
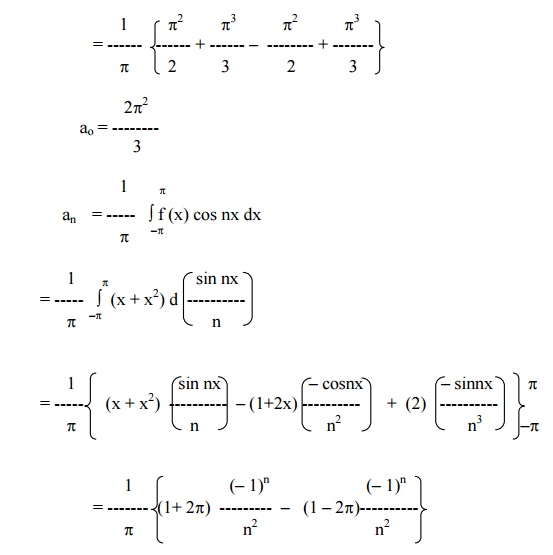
Here x = -pand x = pare the end points of the range. \ The value of FS at x = pis the average of the values of f(x) at x = pand x = -p.
Exercises:
Determine the Fourier expressions of the following functions in the given interval
1.f(x) = (p- x)2, 0 < x < 2p
2.f(x) = 0 in -p< x < 0
= pin 0 < x < p
3.f(x) = x –x2 in [-p,p]
4.f(x) = x(2p-x) in (0,2p)
5.f(x) = sinh ax in [-p, p]
6.f(x) = cosh ax in [-p, p]
7.f(x) = 1 in 0 < x < p
= 2 in p< x < 2p
8.f(x) = -p/4 when -p< x < 0
= p/4 when 0 < x < p
9.f(x) = cosax, in -p< x < p, wherea‟is„ not an integer
10.Obtain a fourier series to represent e-ax from x = -pto x = p. Hence derive the series for p/ sinhp
3 Even and Odd functions
A function f(x) is said to be even if f (-x) = f (x). For example x2, cosx, x sinx, secx are even functions. A function f (x) is said to be odd if f (-x) = - f (x). For example, x3, sin x, x cos x,. are odd functions.
(1) The Euler‟s formula for even function is a
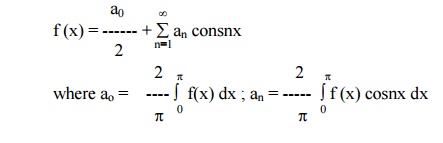
(2) The Euler‟s formula for odd function is
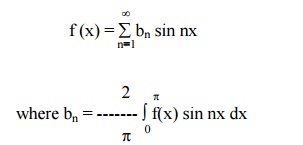
Example 6
Find the Fourier Series for f (x) = x in ( -p, p)
Here, f(x) = x is an odd function.
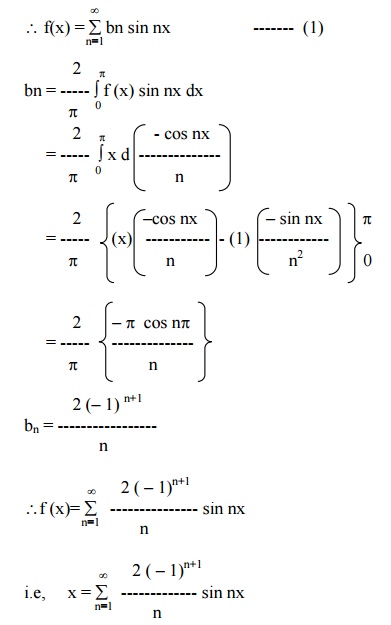
Example 7
Expand f (x) = |x| in (-p, p) as FS and hence deduce that
Example 8
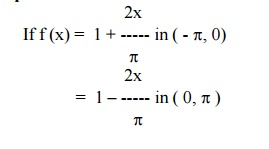
Then find the FS for f(x) and hence show that
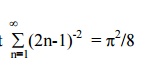
Here f (-x) in (-p,0) = f (x) in (0,p)
f (-x) in (0,p) = f (x) in (-p,0)
f(x) is a even function
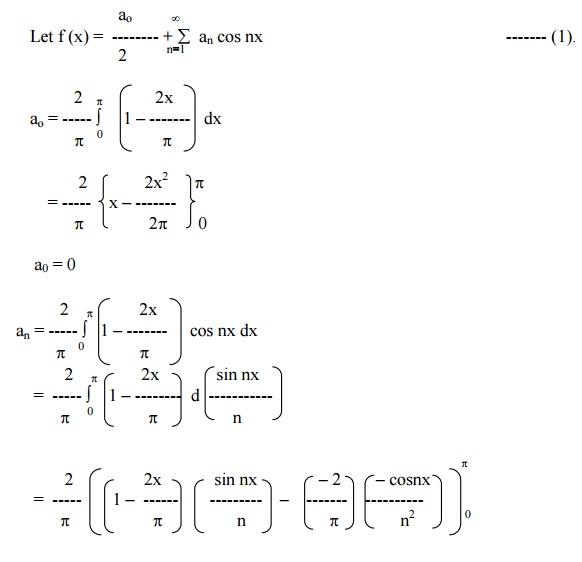
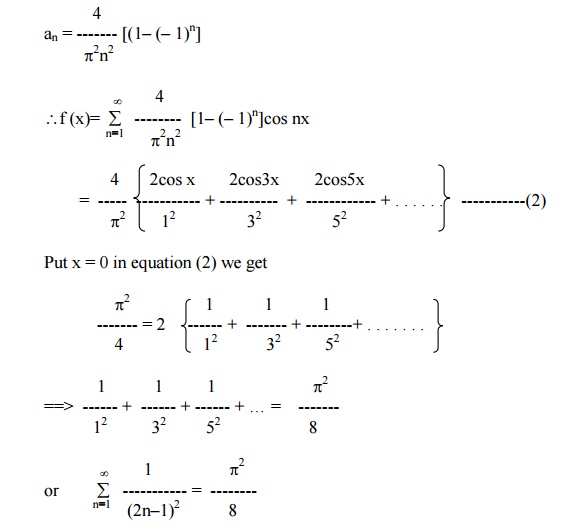
Example 9
Obtain the FS expansion of f(x) = x sinx in (-p< x<p) and hence deduce that
Here f (x) = xsinx is an even function.
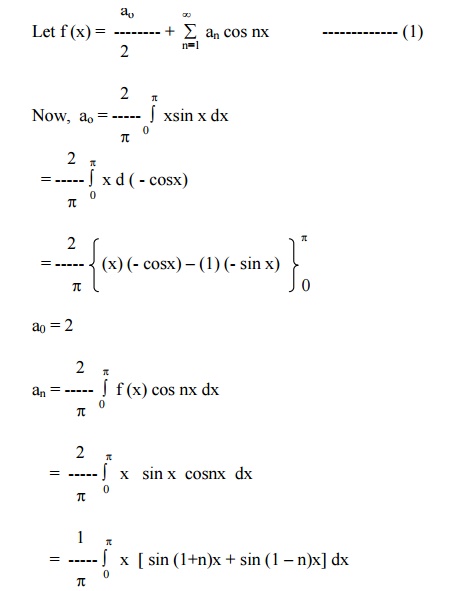
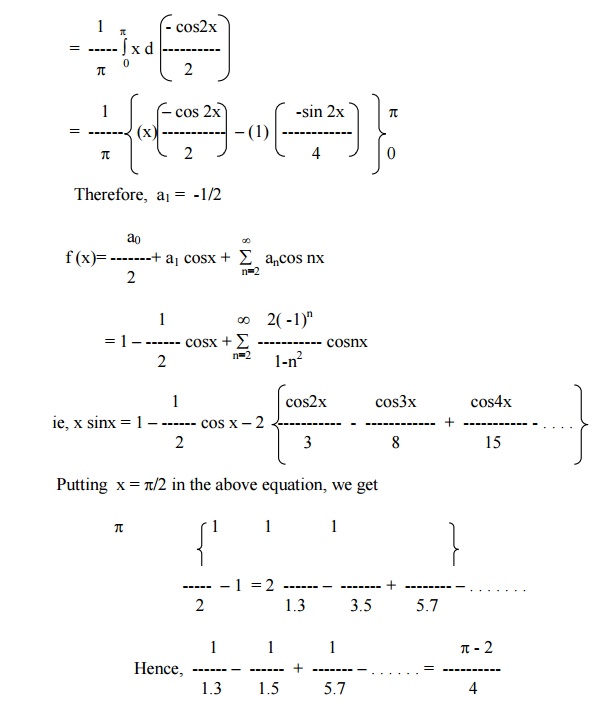
Exercises:
Determine Fourier expressions of the following functions in the given interval:
i. f(x) = p/2 + x, -p< x < 0
p/2 - x, 0 < x < p
ii. f(x) = -x+1 for + -p< x < 0
x+1 for 0 =< x =< p
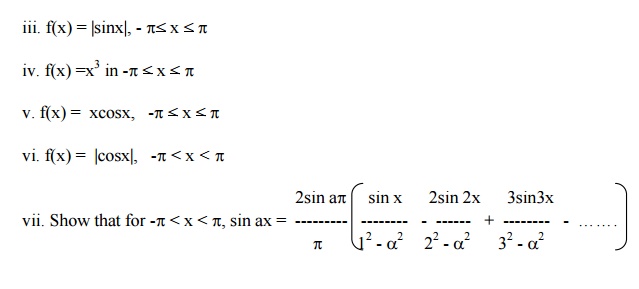
4 HALF RANGE SERIES
It is often necessary to obtain a Fourier expansion of a function for the range (0, p) which is half the period of the Fourier series, the Fourier expansion of such a function consists a cosine or sine terms only.
(i) Half Range Cosine Series
The Fourier cosine series for f(x) in the interval (0,p) is given by
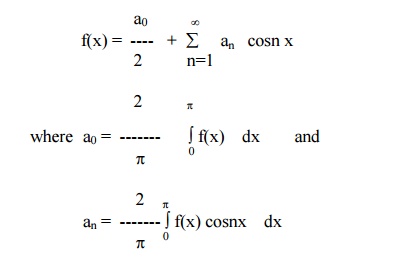
(ii) Half Range Sine Series
The Fourier sine series for f(x) in the interval (0,p) is given by
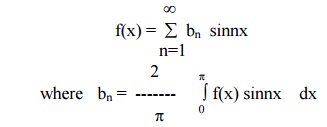
Example 10
If c is the constant in ( 0 < x < p) then show that
c = (4c / p) { sinx + (sin3x /3) + sin5x / 5) + ... ... ... }
Given f(x) = c in (0,p).
Example 11
Find the Fourier Half Range Sine Series and Cosine Series for f(x) = x in the interval (0,p).
Sine Series
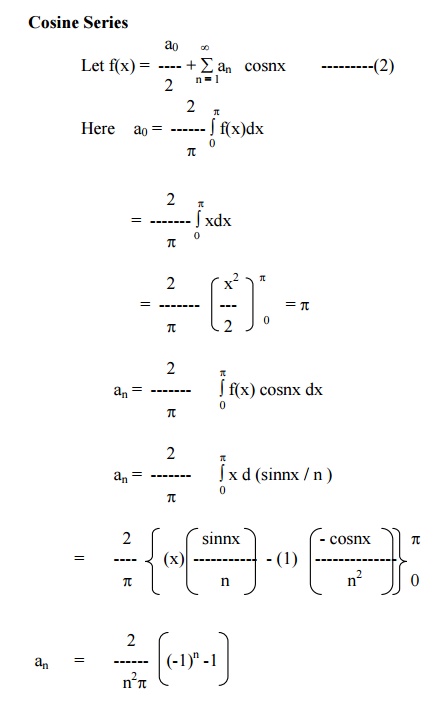
Example 12
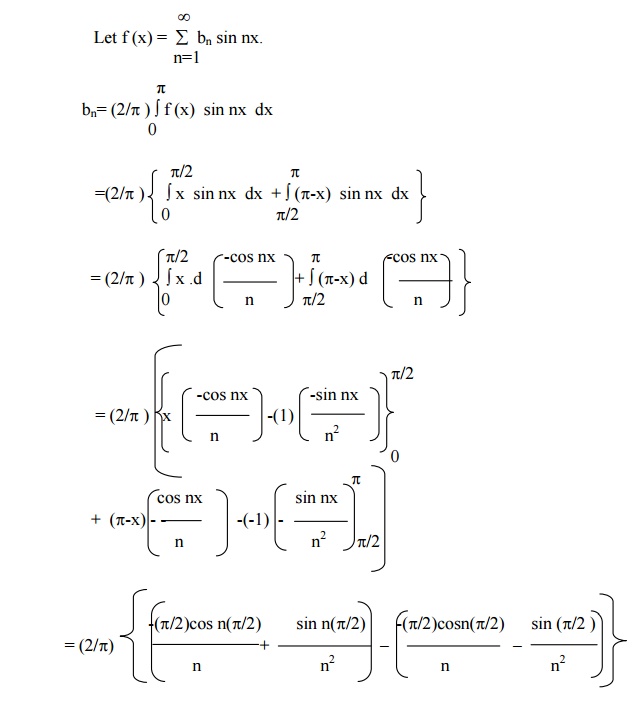
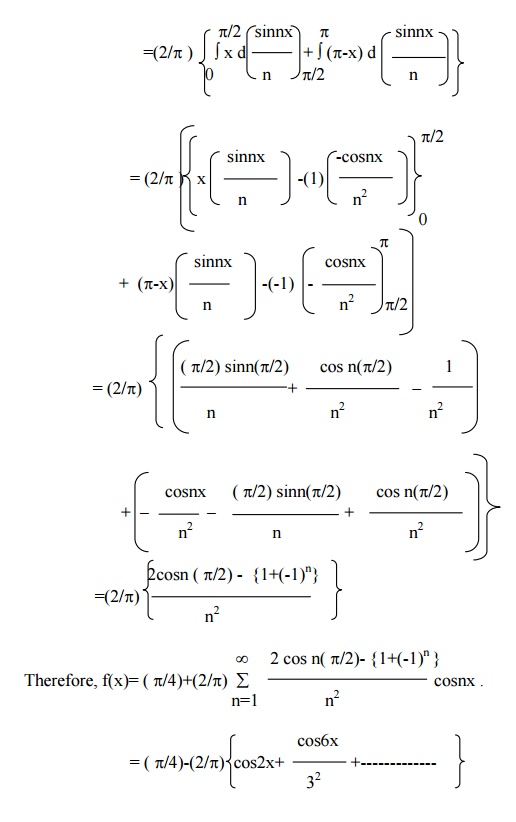
Find the sine and cosine half-range series for the function function . f(x) = x , 0 < x £π/2
= π-x, £x< pπ/2
Sine series
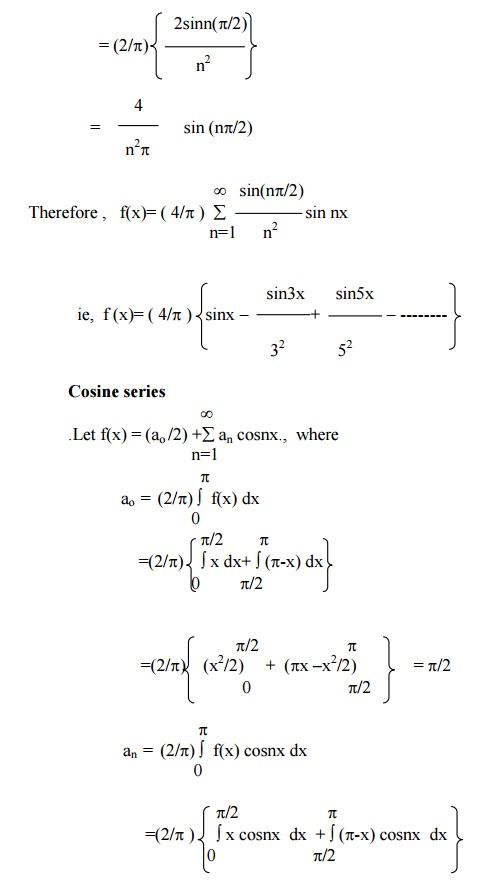
Exercises
1.Obtain cosine and sine series for f(x) = x in the interval 0< x < p. Hence show that 1/12
2.Find the half range cosine and sine series for f(x) = x2 in the range 0 < x < p
3.Obtain the half-range cosine series for the function f(x) = xsinx in (0,p)..
4.Obtain cosine and sine series for f(x) = x (p-x) in 0< x < p 5.Find the half-range cosine series for the function
6.f(x) = (px) / 4 , 0<x< (p/2)
= (p/4)(p-x), p/2 < x < p.
7.Find half range sine series and cosine series for
f(x) = x in 0<x< (p/2)
= 0 in p/2 < x < p.
8.Find half range sine series and cosine series for the function f(x) == p- x in the interval 0 < x < p.
9.Find the half range sine series of f(x) = x cosx in (0,p)
10.Obtain cosine series for
f(x) = cos x , 0<x< (p/2)
= 0, p/2 < x < p.
5 Parseval’s Theorem
Root Mean square value of the function f(x) over an interval (a, b) is defined as
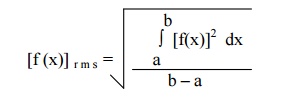
The use of r.m.s value of a periodic function is frequently made in the theory of mechanical vibrations and in electric circuit theory. The r.m.s value is known as the effective value of the function.
Parseval’s Theorem
If f(x) defined in the interval (c, c+2π ), then the Parseval‟s Identity is given by
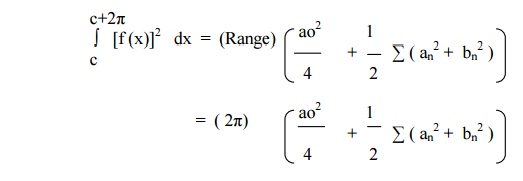
Example 13
Obtain the Fourier series for f(x)
6 CHANGE OF INTERVAL
In most of the Engineering applications, we require an expansion of a given function over an interval 2l other than 2p.
Suppose f(x) is a function defined in the interval c< x < c+2l. The Fourier expansion for f(x) in the interval c<x<c+2l is given by
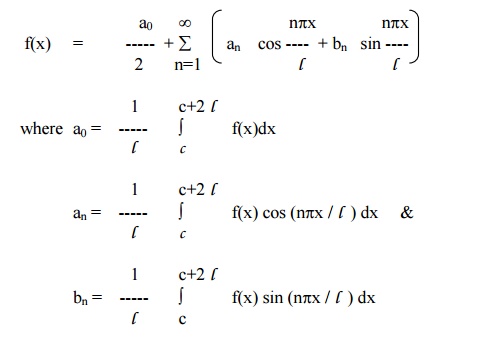
Even and Odd Function
If f(x) is an even function and is defined in the interval ( c, c+2 l ), then
Half Range Series
Sine Series
Cosine series
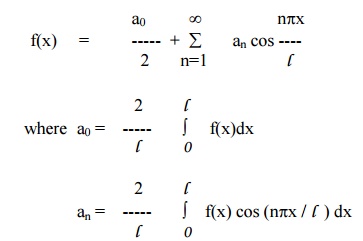
Example 14
Find the Fourier series expansion for the function
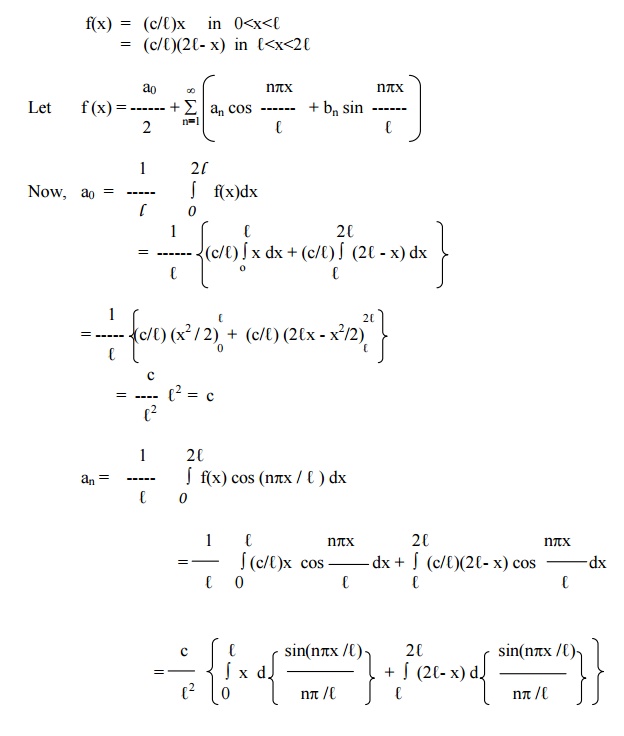
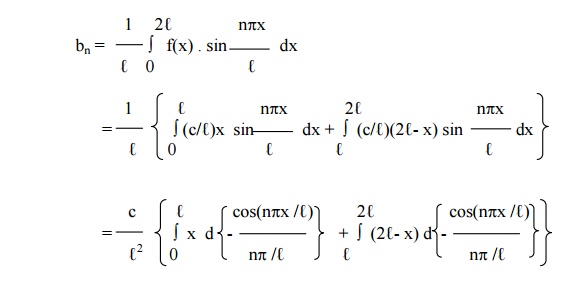
Example 15
Find the Fourier series of periodicity 3 for f(x) = 2x –x2 , in 0 <x <3.
Here 2â„“ = 3.
\ â„“ = 3 / 2.
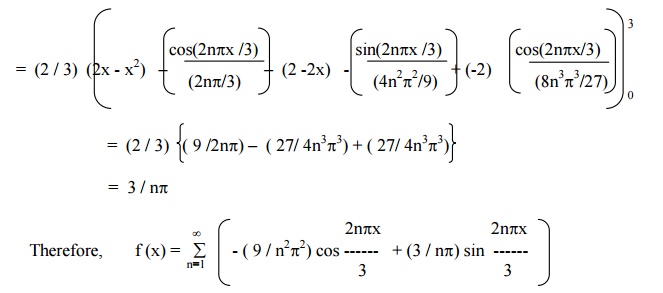
Exercises
1.Obtain the Fourier series for f(x) = px in 0 < x < 2. 2.Find the Fourier series to represent x2 in the interval (-l, l ). 3.Find a Fourier series in (-2, 2), if
f(x) = 0, -2 < x < 0
= 1, 0 < x < 2.
4.Obtain the Fourier series for
f(x) = 1-x in 0 < x < l
= 0 in l < x < 2 l. Hence deduce that
1- (1/3 ) +(1/5) –(1/7) p/4+& … =
2 2 ) + (1/5 2 2
(1/1 ) + (1/3 ) + p…/8) = (
5.If f(x) = px, 0 < x < 1
= p (2-x), 1 < x < 2,
Show that in the interval (0,2),
6.Obtain the Fourier series for
f(x) = x in 0 < x < 1
= 0 in 1 < x < 2
7.Obtain the Fourier series for
f(x) = (cx /l ) in 0 < x < l
= (c/l ) (2 l - x ) in l < x < 2 l .
8.Obtain the Fourier series for
f(x) = (l + x ), - l < x < 0. = (l - x ), 0 < x < l.
10.Express f(x) = x as a half –range sine series in 0 < x < 2
11.Obtain the half-range sine series for ex in 0 < x < 1.
12.Find the half –range cosine series for the function f(x) = (x-2)2 in the interval 0 < x < 2.
7 Harmonic Analysis
The process of finding the Fourier series for a function given by numerical values is known as harmonic analysis.
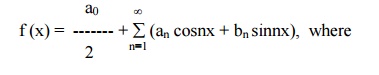
ie, f(x) = (a0/2) + (a1 cosx + b1 sinx) + (a2 cos2x + b2 sin2x) + (a3cos3x + b3sin3x)+-------------…(1)
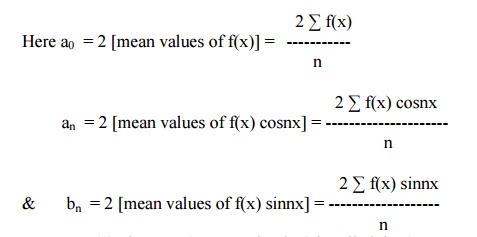
In (1), the term (a1cosx + b1 sinx) is called the fundamental or first harmonic, the term (a2cos2x + b2sin2x) is called the second harmonic and so on.
Example 16
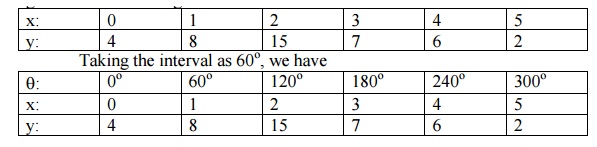
Compute the first three harmonics of the Fourier series of f(x) given by the following table.
We exclude the last point x = 2Ï€.
Let f(x) = (a0/2) + (a1 cosx + b1 sinx) + (a2 cos2x + b2 sin2x) + …………
To evaluate the coefficients, we form the following table.
\ f(x) = 1.45 – 0.37cosx + 0.17 sinx – 0.1cos2x – 0.06 sin2x + 0.033 cos3x+…
Example 17
Obtain the first three coefficients in the Fourier cosine series for y, where y is given in the following table:
\ Fourier cosine series in the interval (0, 2π) is y = (a0 /2) + a1cosq+ a2cos2q+ a3cos3q+ …..
To evaluate the coefficients, we form the following table.
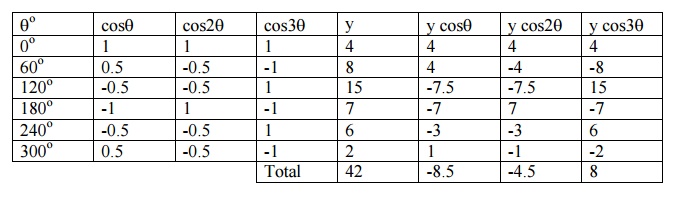
Now, a0 = 2 (42/6) = 14
a1 = 2 ( -8.5/6) = - 2.8
a2 = 2 (-4.5/6) =
a3 = 2 (8/6) = 2.7
y = 7 –2.8 cosq- 1.5 cos2q+ 2.7 cos3q+ …..
Example 18
The values of x and the corresponding values of f(x) over a period T are given below. Show that f(x) = 0.75 + 0.37 cosq+ 1.004 sinq,where q= (2Ï€x )/T
We omit the last value since f(x) at x = 0 is known.
Here q= 2Ï€x / T
When x varies from 0 to T, qvaries from 0 to 2Ï€ with2Ï€/6. an incre
Let f(x) = F(q) = (a0/2) + a1 cosq+ b1 sinq.
To evaluate the coefficients, we form the following table.
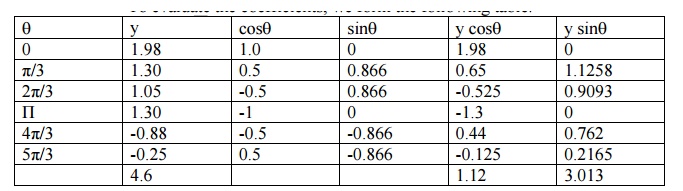
Now, a0 = 2 ( ∑ f(x)/6)=1.5
a1 = 2 (1.12 /6) = 0.37
a2 = 2 (3.013/6) = 1.004
Therefore, f(x) = 0.75 + 0.37 cosq+ 1.004 sinq
Exercises
1.The following table gives the variations of periodic current over a period.
t (seconds) : 0 T/6 T/3 T/2 2T/3 5T/6 T
A (amplitude): 1.98 1.30 1.05 1.30 -0.88 -0.25 1.98
Show that there is a direct current part of 0.75 amp in the variable current and obtain the
amplitude of the first harmonic.
2.The turning moment T is given for a series of values of the crank angle q°=75°
q° : 0 30 60 90 120 150 180
T° : 0 5224 8097 7850 5499 2626 0
Obtain the first four terms in a series of sines to represent T and calculate
T for q= 75°
3. Obtain the constant term and the co-efficient of the first sine and cosine terms in the
Fourier expansionfollowingof table„y‟. as given in th
X : 0 1 2 3 4 5
Y : 9 18 24 28 26 20
4. Find the first three harmonics of Fourier series of y = f(x) from the following data.
X : 0 ° 30° 60° 90° 120° 150° 180° 210° 240° 270° 300° 330°
Y : 298 356373 337 254 15580 516093 147 221
2.8 Complex Form of Fourier Series
The series for f(x) defined in the interval (c, c+2Ï€)and satisfying
8 Complex Form of Fourier Series
The series for f(x) defined in the interval (c, c+2Ï€)and satisfying
Dirichlet‟s conditions can be given in the form of
In the interval (c, c+2â„“), the complex form of Fourier series is given by
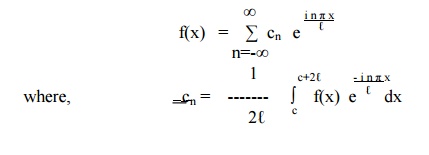
Example 19
Find the complex form of the Fourier series f(x) = e –x in -1 ≤ x ≤ 1.
Example 20
Find the complex form of the Fourier series f(x) = ex in - π < x< π.
Exercises
Find the complex form of the Fourier series of the following functions.
1.f(x) = eax, -l < x < l.
2.f(x) = cosax, -p< x < p.
3.f(x) = sinx, 0 < x < p.
4.f(x) = e-x, -1 < x < 1.
5.f(x) = sinax, a is not an integer in (-p, p).
9 SUMMARY(FOURIER SERIES)
A Fourier series of a periodic function consists of a sum of sine and cosine terms. Sines and cosines are the most fundamental periodic functions.The Fourier series is named after the French Mathematician and Physicist Jacques Fourier (1768 –1830). Fourier series has its application in problems pertaining to Heat conduction, acoustics, etc. The subject matter may be divided into the following sub topics.
FORMULA FOR FOURIER SERIES
Consider a real-valued function f(x) which obeys the following conditions called
Dirichlet‟s conditions :
1. f(x) is defined in an interval (a,a+2l), and f(x+2l) = f(x) so that f(x) is a periodic function of period 2l.
2. f(x) is continuous or has only a finite number of discontinuities in the interval (a,a+2l).
3. f(x) has no or only a finite number of maxima or minima in the interval (a,a+2l).
Also, let
is called the Fourier series of f(x) in the interval (a,a+2l). Also, the real numbers a0, a1, a2, ….an, and b1, b2 , ….bn are called the Fourier coefficients of f(x). The formulae (1), (2) and (3) are called Euler‟s formulae.
It can be proved that the sum of the series (4) is f(x) if f(x) is continuous at x. Thus we have
Suppose f(x) is discontinuous at x, then the sum of the series (4) would
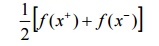
where f(x+) and f(x-) are the values of f(x) immediately to the right and to the left of f(x) respectively.
Particular Cases Case (i)
Suppose a=0. Then f(x) is defined over the interval (0,2l). Formulae (1), (2), (3) reduce to
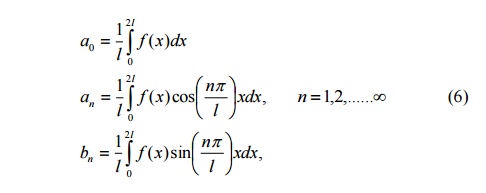
Then the right-hand side of (5) is the Fourier expansion of f(x) over the interval (0,2l).
If we set l=p, then f(x) is defined over the interval (0,2p). Formulae (6) reduce to
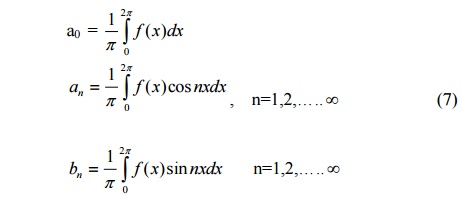
Also, in this case, (5) becomes
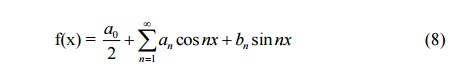
Case (ii)
Suppose a=-l. Then f(x) is defined over the interval (-l , l). Formulae (1), (2) (3) reduce to
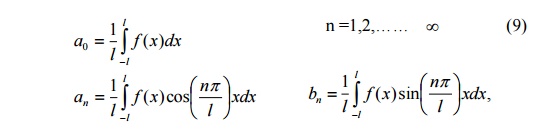
Then the right-hand side of (5) is the Fourier expansion of f(x) over the interval (-l , l).
If we set l = p, then f(x) is defined over the interval (-p, p). Formulae (9) reduce to
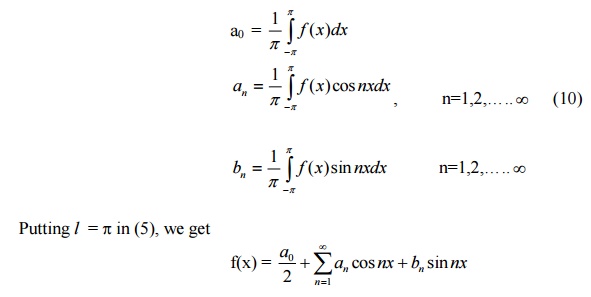
Some useful results :
1. The following rule called Bernoulli‟seful in evaluating the Fourier coefficients.
2. The following integrals are also useful :
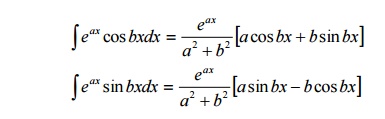
3. If „n‟ is integer, then
sin np= 0 , cosnp= (-1)n , sin2np= 0, cos2np=1
ASSIGNMENT
1. The displacement y of a part of a mechanism is tabulated with corresponding angular movement x0 of the crank. Express y as a Fourier series upto the third harmonic.
x0 0 30 60 90 120 150 180 210 240 270 300 330
Y 1.80 1.10 0.30 0.16 1.50 1.30 2.16 1.25 1.30 1.52 1.76 2.00
2. Obtain the Fourier series of y upto the second harmonic using the following table :
x0 45 90 135 180 225 270 315 360
y 4.0 3.8 2.4 2.0 -1.5 0 2.8 3.4
3. Obtain the constant term and the coefficients of the first sine and cosine terms in the Fourier expansion of y as given in the following table :
x 0 1 2 3 4 5
y 9 18 24 28 26 20
4. Find the Fourier series of y upto the second harmonic from the following table :
x 0 2 4 6 8 10 12
Y 9.0 18.2 24.4 27.8 27.5 22.0 9.0
5. Obtain the first 3 coefficients in the Fourier cosine series for y, where y is given below
x 0 1 2 3 4 5
y 4 8 15 7 6 2
Related Topics