Half Range Series

HALF RANGE SERIES

It is often necessary to obtain a Fourier expansion of a function for the range (0, p) which is half the period of the Fourier series, the Fourier expansion of such a function consists a cosine or sine terms only.

(i) Half Range Cosine Series

The Fourier cosine series for f(x) in the interval (0,p) is given by

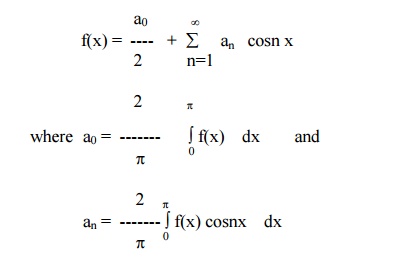
(ii)    Half Range Sine Series 

The Fourier sine series for f(x) in the interval (0,p) is given by

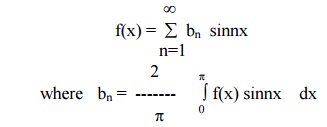
Example 10

If  c is the constant in ( 0 < x < p) then show that

c = (4c / p)  { sinx + (sin3x /3) + sin5x / 5) + ... ... ... }

Given   f(x) = c in (0,p).

Example 11

Find the Fourier Half Range Sine Series and Cosine Series for f(x) = x in the interval (0,p).

Sine Series

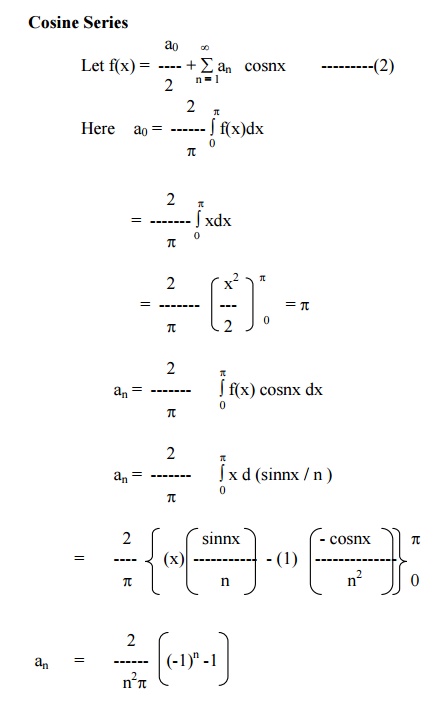
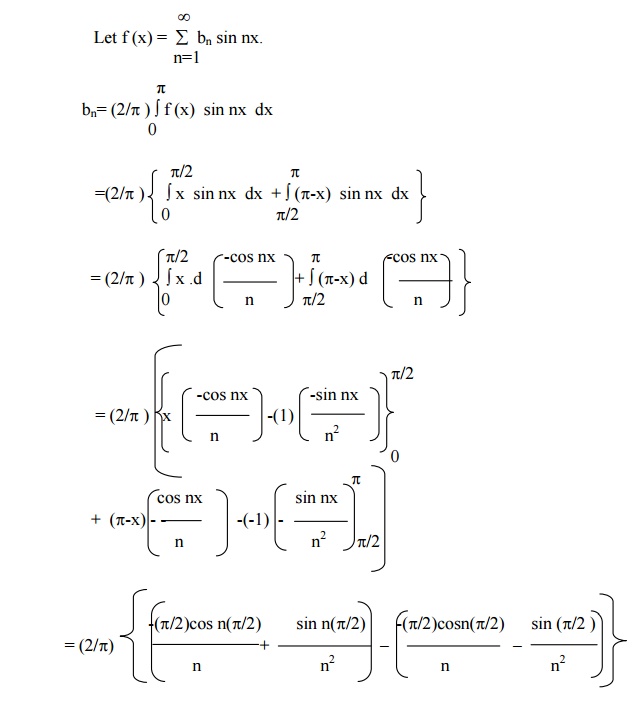
Example 12

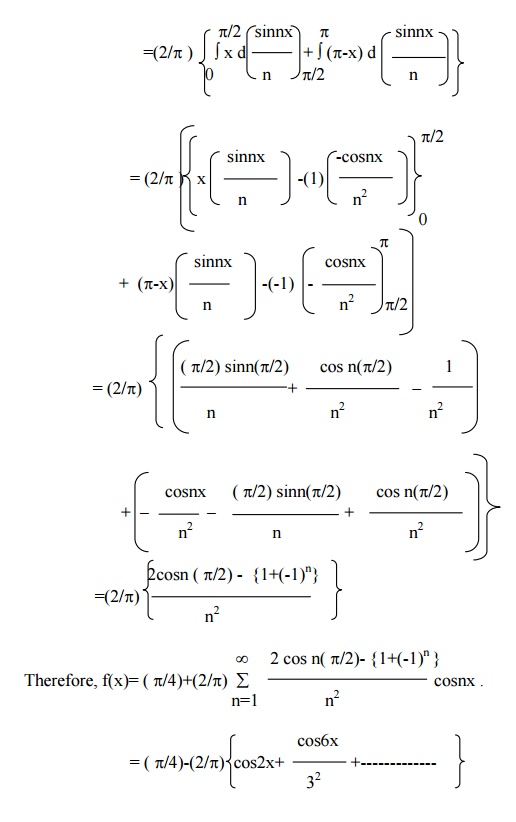
Find the sine and cosine half-range series for the function function . f(x) = x , 0 < x Â£Ï€/2

= Ï€-x,  Â£x< pÏ€/2

Sine series

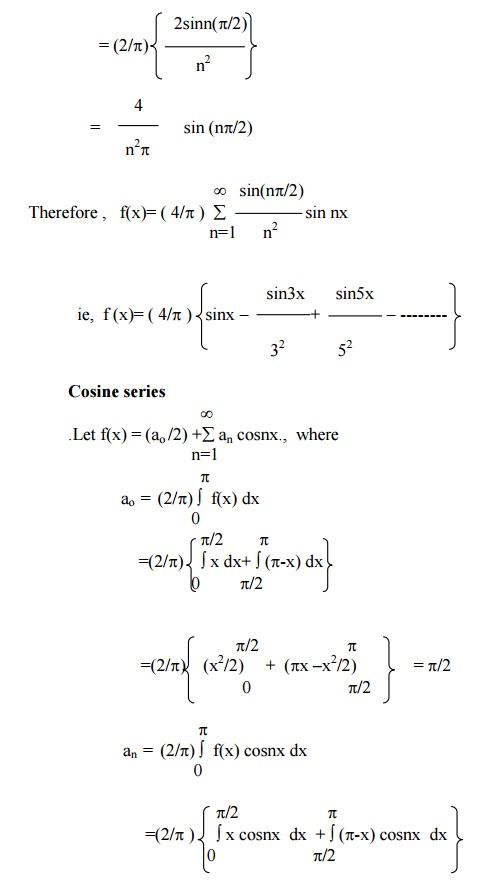
Exercises

1.Obtain cosine and sine series for f(x) = x in the interval 0< x < p. Hence show that 1/12

2.Find the half range cosine and sine series for f(x) = x2 in the range 0 < x < p

3.Obtain the half-range cosine series for the function f(x) = xsinx in (0,p)..

4.Obtain cosine and sine series for f(x) = x (p-x) in 0< x < p 5.Find the half-range cosine series for the function

6.f(x) = (px) / 4 , 0<x< (p/2)

= (p/4)(p-x), p/2 < x < p.

7.Find half range sine series and cosine series for

f(x) = x in  0<x< (p/2)

= 0 in  p/2 < x < p.

8.Find half range sine series and cosine series for the function f(x) == p- x in the interval 0 < x < p.

9.Find the half range sine series of f(x) = x cosx in (0,p)

10.Obtain cosine series for

f(x) = cos x ,   0<x< (p/2)

=   0,  p/2 < x < p.