Chapter: Mathematics (maths) : Fourier Series
Important Questions and Answers: Fourier Series
FOURIER SERIES
1. Explain periodic function with
examples.
A function f (x)is said to have a period T if for all x ,
f (x
+T
)=f
(x), where T is a
positive constant. The least value of T >0 is called the period of f (x).
Example : f
(x)=sin x ; f (x +2p) sin=(x 2 +p) sin=x .
2. State Dirichlet’s conditions for a function to be expanded as a Fourier series.
Let a function f
( x) be defined in the interval c <x
<c
2+p with period 2p and satisfies the following conditions can be
expanded as a Fourier series in (c, c +2p)
.
(i)
f (x)
is a well defined function.
(ii)
f (
x) is finite or bounded.
(iii)
f (
x) has only a finite number of discontinuous point.
(iv)
f (
x) has only a finite number of maxima and minima.
3. State
whether y =tan x can be expressed as a Fourier
series. If so how?. If not why?
tan
x cannot be
expanded as a
Fourier series. Since
tan x not satisfies
D
condition.
4. State
the convergence condition on Fourier series.
(i) The
Fourier series of f ( x) converges to f ( x) at all
points where f ( x) is continuous.
(ii) At
a point of discontinuity x0 , the series converges to the
average of the left limit and right limit
of
f (x) at x0
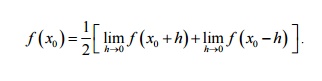
5. To
what value does the sum of Fourier series of
f (x)
converge at the point of continuity
x =a ?
The
sum of Fourier series of f (x)
converges to the value f (a)
at the continuous point
x =a
.
6. To what value does the sum of Fourier
series of f (
x) converge at the point of discontinuity x =a ?
At the discontinuous point x =a , the sum of
Fourier series of f ( x)
converges to


\ sinh
x is an odd function.
\ a0 =0,
an =0.
10. Write the formulae for Fourier
constants for f
(
x) in the interval (-p, p).
The Fourier constants for f (x) in the interval (-p,
p)are given by
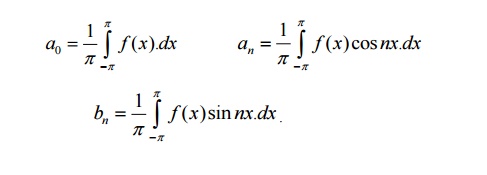
11. Find the constant a0
of the Fourier series for function f
(x)=x in 0
ÂŁx
ÂŁ2p.
The given function f ( x ) = |x| is an even function.

14. Find bn in the
expansion of x2 as a Fourier series in (-p,p).
Since
f ( x ) =x2 is an even function, the value of bn =0
15. Find the constant term a0 in the Fourier series corresponding to f (x
)= x
-x3 in
(-Ď€,
Ď€).
Given f (x)=x -x3
f
(-x)=-x +x3 =-(x-x3
)=-f (x)
i.e, f (-x)=-f (x)
\
f (
x) is an odd function in (-p,p)
Hence
a0 =0 .
16. If
f (x)=x
2 -x4 is expanded as a Fourier series in (-l,l ), find the value of bn
.

The coefficient of sin nx , bn
=0 . Since the Fourier
series of f ( x) consists of cosine terms only.
18. Find the constant a0 of the Fourier series for the function f (x) = xcosx in - π < x < π.
-Ď€ < x <. Î
f ( x ) =x cos x
f
(
-x ) =x-cos x =f(x-)
\ f
(
x) is an odd function. Hence
a0 =0 .
19.
Write the Fourier sine series of k
in (0,p).

20. Obtain the sine series for unity in
(0, π).
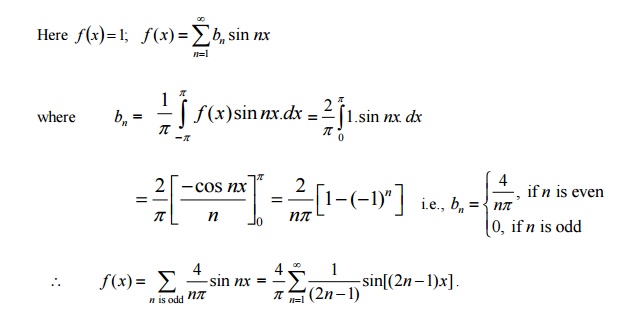
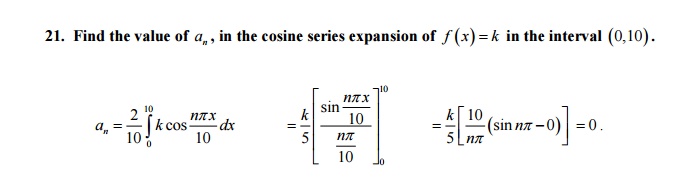
22. If
f (x)is
defined in -3 ÂŁx 3ÂŁwhat is the value of Fourier coefficients.
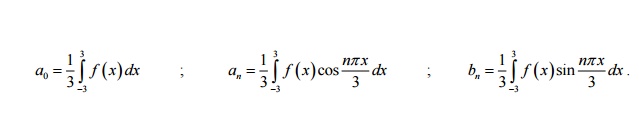
23. Define Root Mean Square value of a
function.
The
root mean square value of y =f ( x) in (a
, b) is denoted by y . It is defined as

24. Find the R.M.S value of y
=x
2 in
(-p, p).
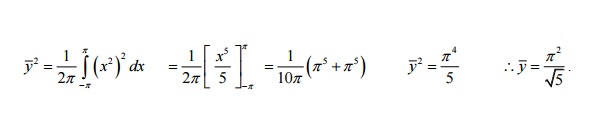
25. Find the R.M.S value if f ( x ) = x2 in -Ď€
ÂŁx
ÂŁ.Ď€
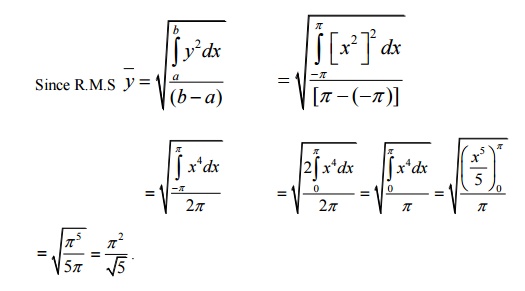
26. State the
Parseval’s Identity (or)
theorem
If f (
x) is a periodic function of
period 2p in (c, c +2p)
with Fourier coefficients

27. Write the complex form of Fourier
series for f(x) defined in the interval (c, c+2l).
The series for f (x) defined in the interval (c, c +2p) and satisfying Dirichlet’s conditions can be given in the form of
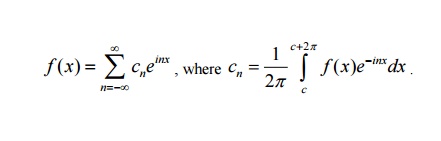
28. What do you mean by Harmonic
analysis?
The process of finding the Fourier series of the periodic function y =f (x)of period 2l (or )2p using the numerical values of x and yBar is known as Harmonic analysis.
PART B

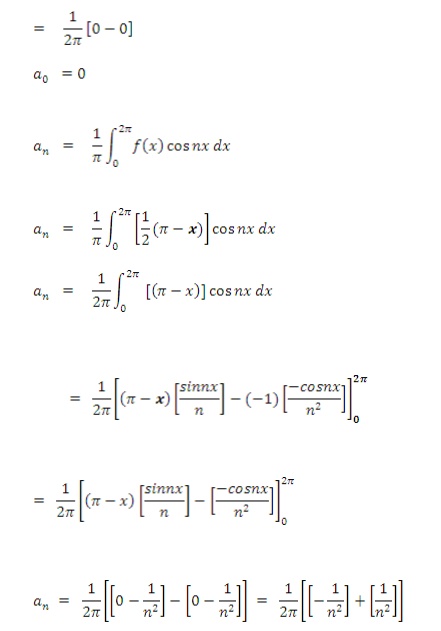
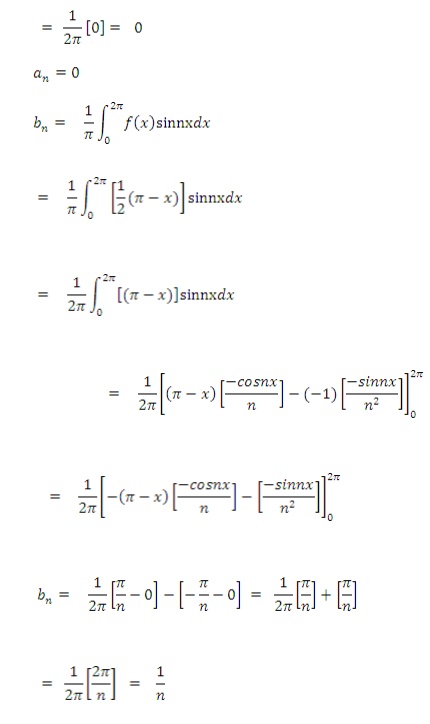
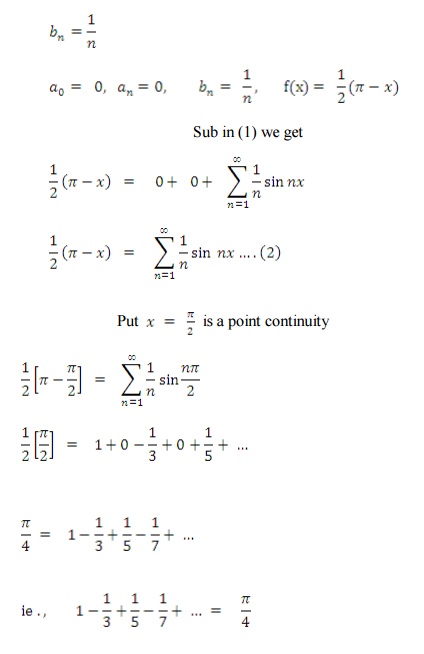
2) Obtain Fourier series for f(x) of
period 2l and defined as follows

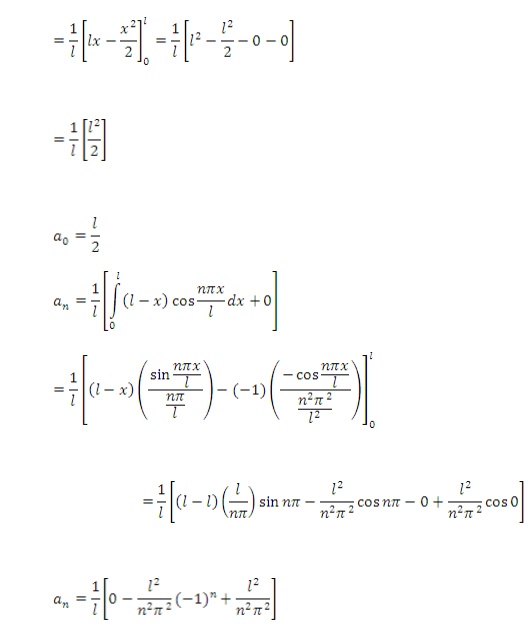
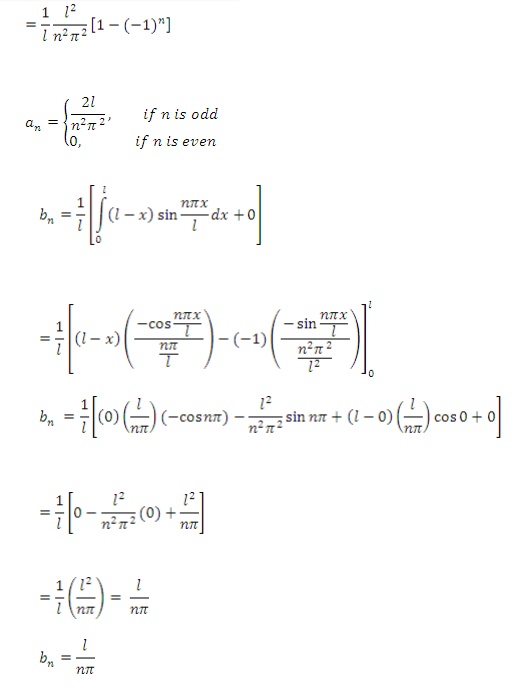
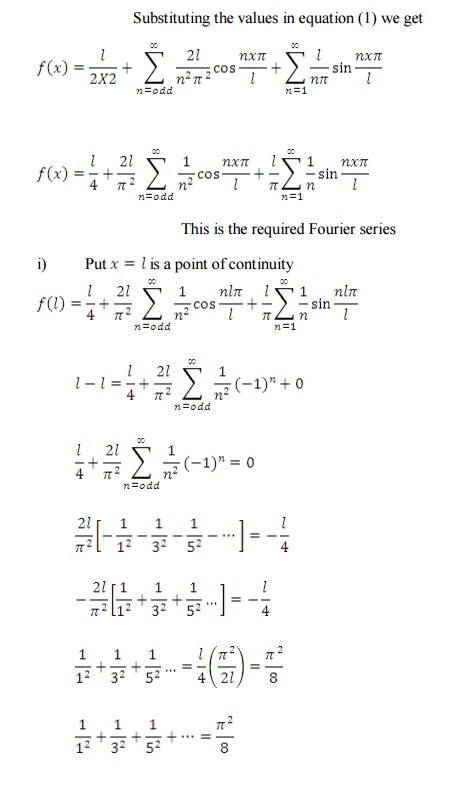
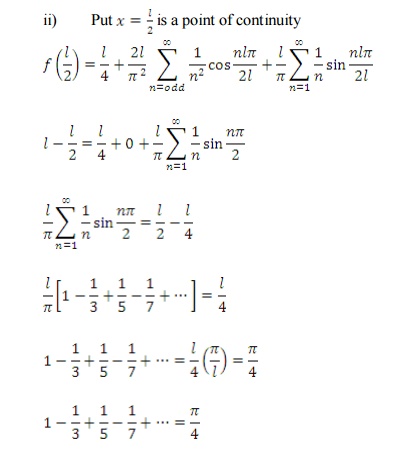
Hence
proved
ODD AND EVEN FUNCTION
3.
Find the Fourier series of
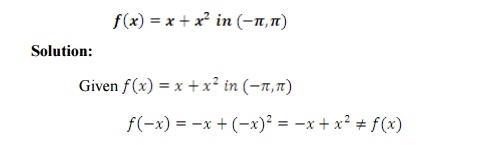
Therefore
f(x) is neither even nor odd function
We know that the Fourier series is
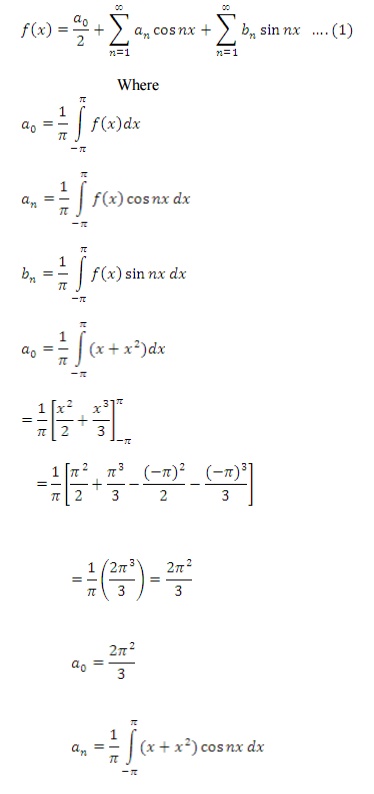
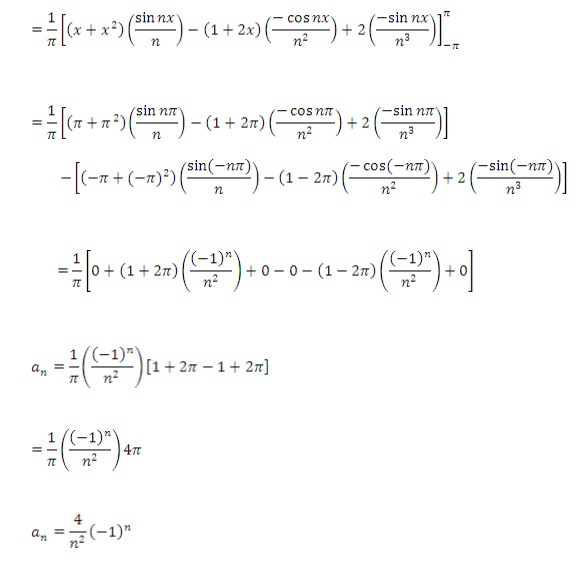
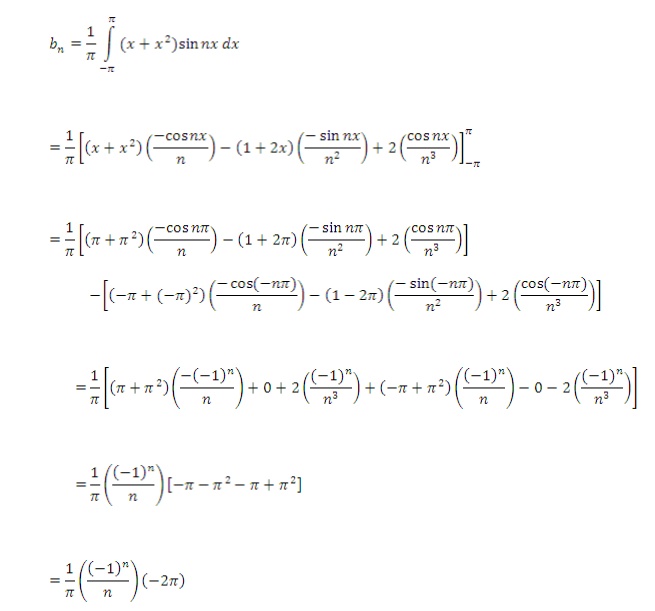

FOURIER SINE SERIES


This
is the required half range Fourier sine series.
HALF
RANGE COSINE SERIES
4)
Obtain the half range cosine series
for f(x)=(x-2)2 in the interval (0,2).
olution:
Given
f(x)=(x-2)2
We know that the Fourier half range cosine series is
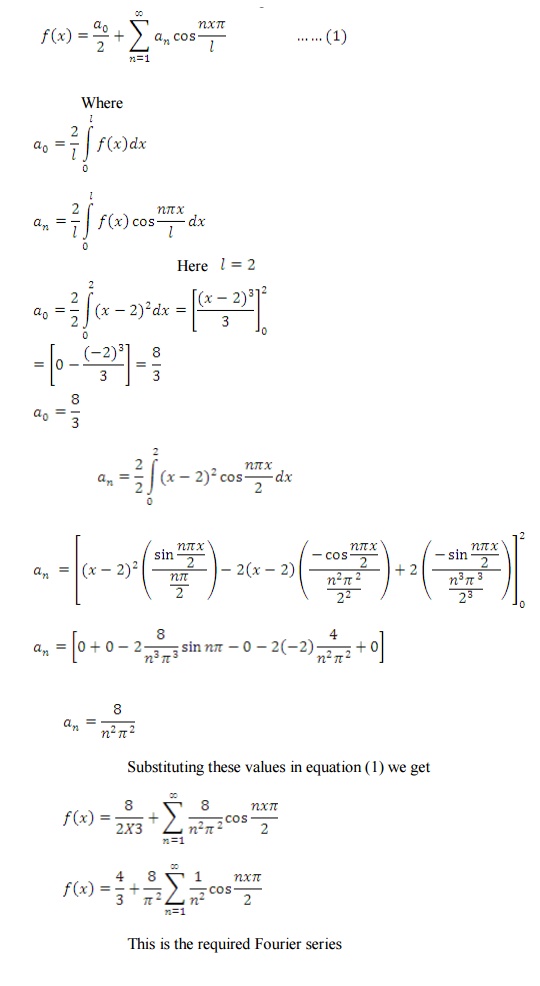
This is the required Fourier series
COMPLEX
FORM OF FOURIER SERIES
6) Find the complex form of the Fourier series of

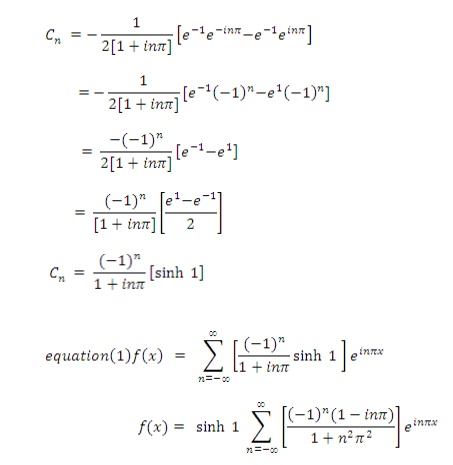
HARMONIC
ANALYSIS
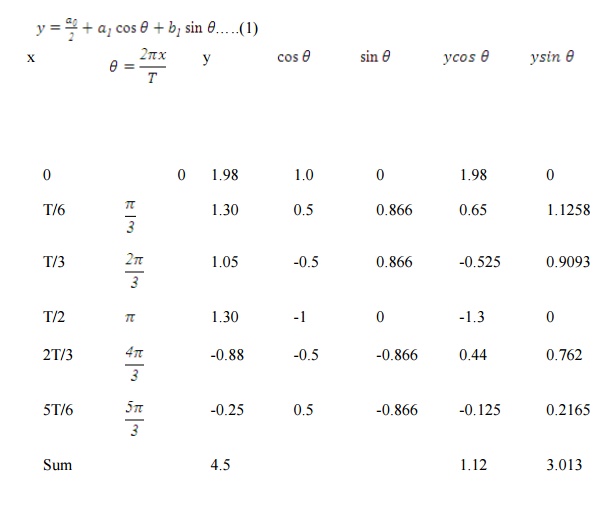
7)Computeupto first harmonics of the
Fourier series of f(x) given by the following table
X 0 T/6 T/3 T/2 2T/3 5T/6 T
F(x) 1.98 1.3 1.05 1.3 -0.88 -0.25 1.98
Solution:
First and last value are
same. Hence we omit the last value.
When x varies from 0 to T
varies from 0 to 2p
We know that the Fourier
series is
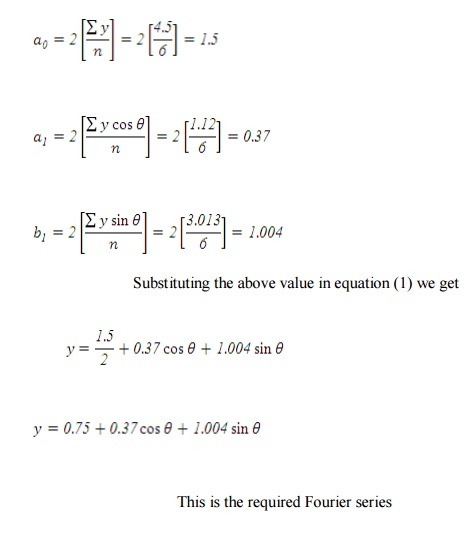
Related Topics