Formula For Fourier Series

A Fourier series of a periodic function consists of a sum of sine and cosine terms. Sines and cosines are the most fundamental periodic functions.The Fourier series is named after the French Mathematician and Physicist Jacques Fourier (1768 –1830). Fourier series has its application in problems pertaining to Heat conduction, acoustics, etc. The subject matter may be divided into the following sub topics.

FORMULA FOR FOURIER SERIES

Consider a real-valued function f(x) which obeys the following conditions called

Dirichlet‟s conditions   :

1.     f(x) is defined in an interval (a,a+2l), and f(x+2l) = f(x) so that f(x) is a periodic function of period 2l. 

2.     f(x) is continuous or has only a finite number of discontinuities in the interval (a,a+2l). 

3.     f(x) has no or only a finite number of maxima or minima in the interval (a,a+2l).

Also, let

is called the Fourier series of f(x) in the interval (a,a+2l). Also, the real numbers a0, a1, a2, ….an, and b1, b2 , ….bn are called the Fourier coefficients of f(x). The formulae (1), (2) and   (3)   are   called   Euler‟s   formulae.

It can be proved that the sum of the series (4) is f(x) if f(x) is continuous at x. Thus we have

Suppose f(x) is discontinuous at x, then the sum of the series (4) would

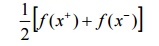
where f(x+) and f(x-) are the values of f(x) immediately to the right and to the left of f(x) respectively.

Particular Cases Case (i)

Suppose a=0. Then f(x) is defined over the interval (0,2l). Formulae (1), (2), (3) reduce to

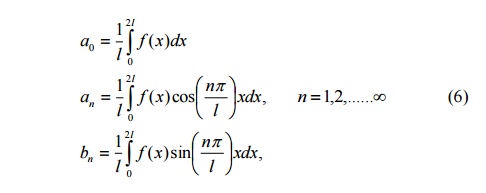
Then the right-hand side of (5) is the Fourier expansion of f(x) over the interval (0,2l).

If we set l=p, then f(x) is defined over the interval (0,2p). Formulae (6) reduce to

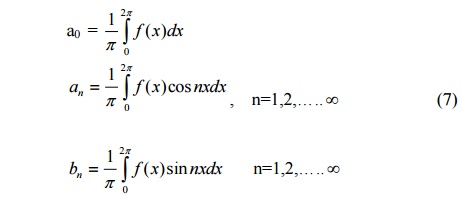
Also, in this case, (5) becomes

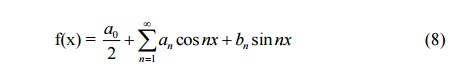
Case (ii)

Suppose a=-l. Then f(x) is defined over the interval (-l , l). Formulae (1), (2) (3) reduce to

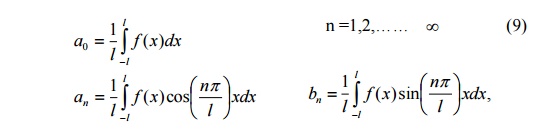
Then the right-hand side of (5) is the Fourier expansion of f(x) over the interval (-l , l).

If we set l = p, then f(x) is defined over the interval (-p, p).  Formulae (9) reduce to

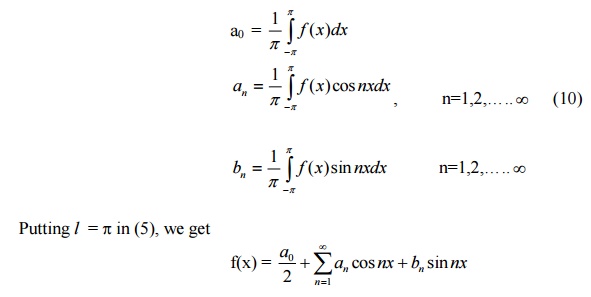
Some useful results :

1.     The   following   rule   called   Bernoulli‟seful in evaluating the Fourier coefficients.

2.       The following integrals are also useful : 

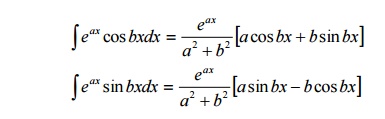
3.                                         If   â€žn‟   is   integer,   then 

sin np= 0 ,       cosnp= (-1)n ,        sin2np= 0,  cos2np=1