Chapter: Mathematics (maths) : Applications of Partial Differential Equations
Applications of Partial Differential Equations
APPLICATIONS OF PARTIAL DIFFERENTIAL EQUATIONS
1 INTRODUCTION
2 SOLUTION OF WAVE EQUATION
3 SOLUTION OF THE HEAT EQUATION
4 SOLUTION OF LAPLACE EQUATIONS
1 INTRODUCTION
In Science and Engineering problems, we always seek a solution of the differential equation which satisfies some specified conditions known as the boundary conditions. The differential equation together with the boundary conditions constitutes a boundary value problem. In the case of ordinary differential equations, we may first find the general solution and then determine the arbitrary constants from the initial values. But the same method is not applicable to partial differential equations because the general solution contains arbitrary constants or arbitrary functions. Hence it is difficult to adjust these constants and functions so as to satisfy the given boundary conditions. Fortunately, most of the boundary value problems involving linear partial differential equations can be solved by a simple method known as the method of separation of variables which furnishes particular solutions of the given differential equation directly and then these solutions can be suitably combined to give the solution of the physical problems.
2Solution of the wave equation
The wave equation is
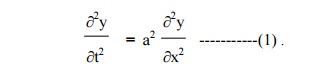
Let y = X(x) . T(t) be the solution of (1), where „X‟ is a function of „x‟ only and „T‟ is a function of „t‟ only.
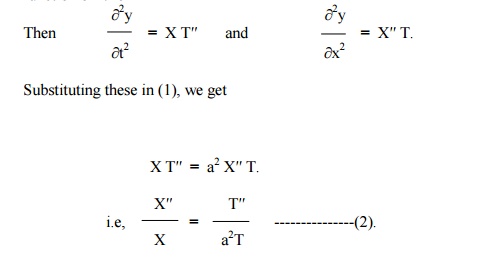
Of these three solutions, we have to select that particular solution which suits the physical nature of the problem and the given boundary conditions. Since we are dealing with problems on vibrations of strings, „y‟ must be a periodic function of „x‟ and „t‟.

Now the left side of (2) is a function of „x‟ only and the right side is a function of „t‟ only.
Since „x‟ and „t‟ are independent variables, (2) can hold good only if each side is equal to a constant.
Hence the solution must involve trigonometric terms.
Therefore, the solution given by (5),
i.e, y = (c5 coslx + c6 sin lx) (c7 cosalt+ c8 sin alt)
is the only suitable solution of the wave equation.
llustrative Examples.
Example 1
If a string of length â„“ is initially at rest in equilibrium position and each of its points is given the velocity
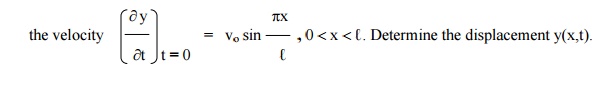
Solution
The displacement y(x,t) is given by the equation
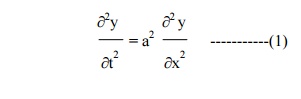
The boundary conditions are
i. y(0,t) = 0, for t Âł0.
ii. y(â„“,t) Âł0.= 0, for t
y(x,0) = 0, for 0 ÂŁx ÂŁâ„“.
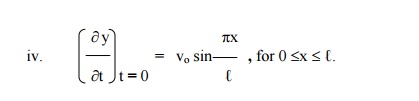
Since the vibration of a string is periodic, therefore, the solution of (1) is of the form
y(x,t) = (Acoslx + Bsinlx)(Ccoslat + Dsinlat) ------------(2)
Using (i) in (2) , we get
0 = A(Ccoslat + Dsinlat) , for all t Âł0.
Therefore, A = 0
Hence equation (2) becomes
y(x,t) = B sinlx(Ccoslat + Dsinlat) ------------ (3)
Using (ii) in (3), we get
0 = Bsinlâ„“ (Ccoslat+Dsinlat), for all t Âł0, which gives lâ„“ = n
Hence, l= np / l , n being an integer.

Using condition (iv) in the above equation, we get

Example 2
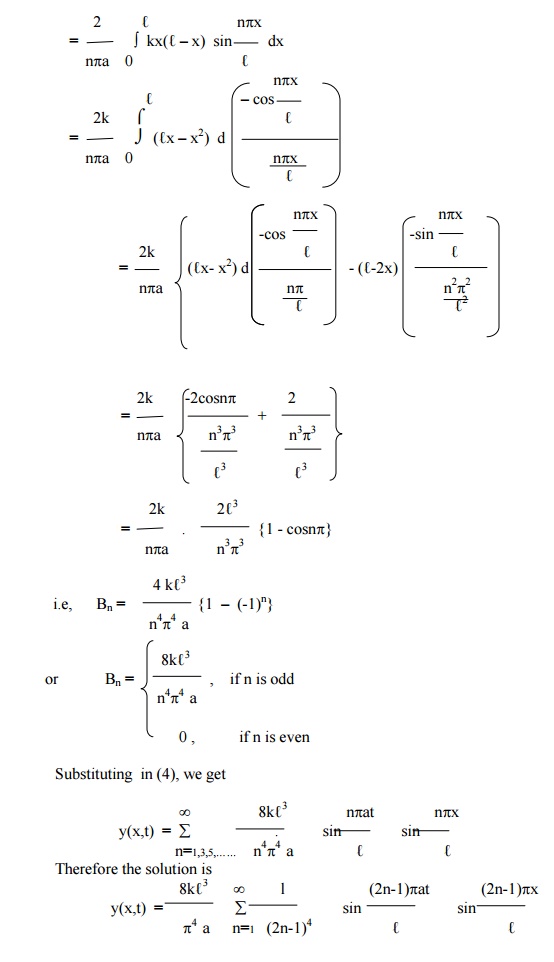
A tightly stretched string with fixed end points x = 0 & x = â„“ is initially at rest in its equilibrium position . If it is set vibrating by giving to each of its points a velocity
¶y/¶t = kx(ℓ-x) at t = 0. Find the displacement y(x,t).
Solution
The displacement y(x,t) is given by the equation
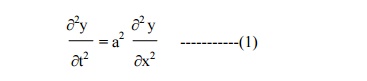
The boundary conditions are


Example 3
A tightly stretched string with fixed end points x = 0 & x = â„“ is initially in a position given by y(x,0) = y0sin3(px/â„“). If it is released from this position, find the displacement y at any time and at any distance from the end x = 0 .
Solution
The displacement y(x,t) is given by the equation
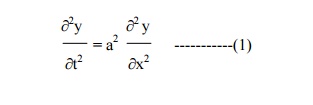
The boundary conditions are
(i) y(0,t) = 0, "t Âł0.
(ii) y("tâ„“Âł,t)0. = 0,
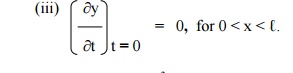
(iv) y(x,0) = y0 sin3((px/â„“), for 0 < x < â„“.
The suitable solution of (1) is given by
y(x,t) = (Acoslx + Bsinlx)(Ccoslat + Dsinlat) ------------(2)
Using (i) and (ii) in (2) , we get


Example 4
A string is stretched & fastened to two points x = 0 and x = â„“ apart. Motion is started by displacing the string into the form y(x,0) = k(â„“x-x2) from which it is released at time t = 0. Find the displacement y(x,t).
Solution
The displacement y(x,t) is given by the equation
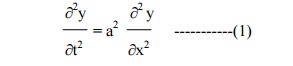
The boundary conditions are
(i) y(0,t) = 0, "t Âł0.
(ii) y(â„“,t) "t Âł=0. 0,
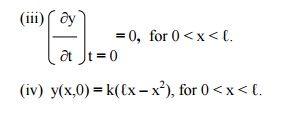
The suitable solution of (1) is given by
y(x,t) = (Acoslx + Bsinlx)(Ccoslat + Dsinlat) ------------(2)
Using (i) and (ii) in (2) , we get

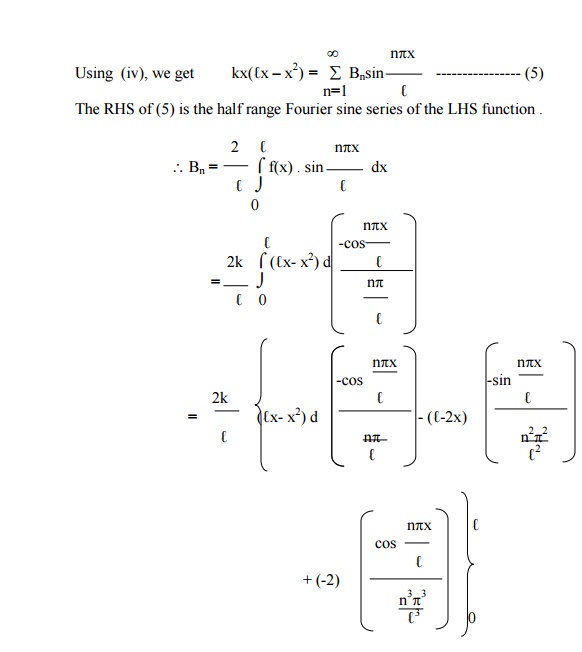

Example 5
Solution
The displacement y(x,t) is given by the equation
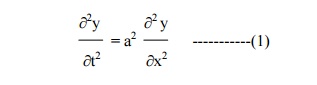
The suitable solution of (1) is given by
y(x,t) = (Acoslx + Bsinlx)(Ccoslat + Dsinlat) ------------(2)
The boundary conditions are
(i) y(0,t) = 0, "t Âł0.
(ii) y(â„“,t) "t Âł=0. 0,
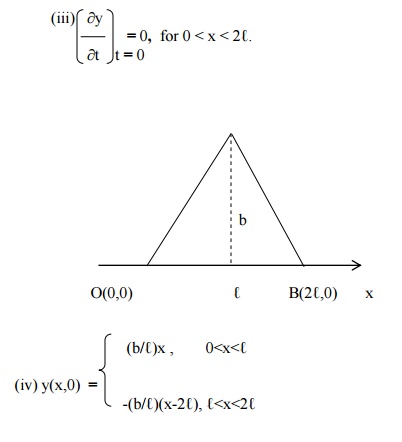
[Since, equation of OA is(y- b)/(oy-b)== (x(b/-â„“)/(2â„“-â„“)x)]â„“
Using conditions (i) and (ii) in (2), we get

Here B can not be zero, therefore D = 0.
Hence equation (3) becomes

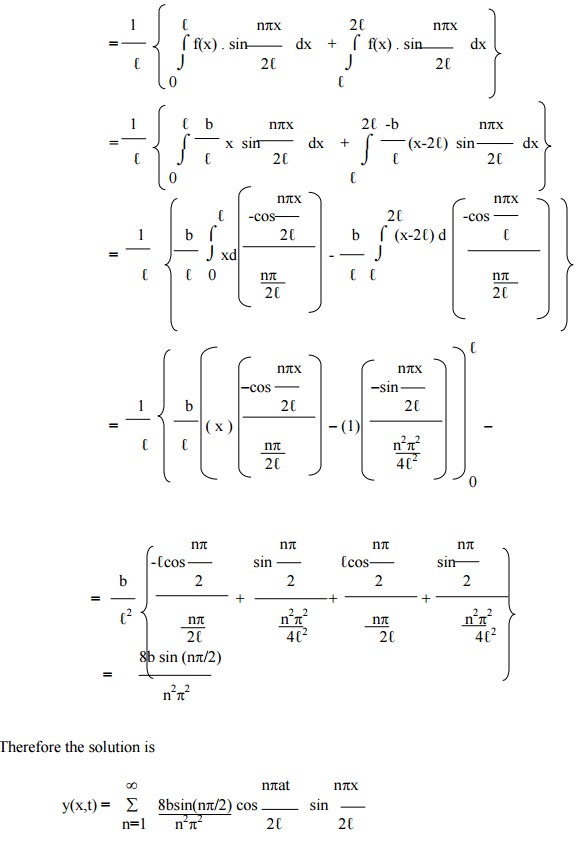
Example 6
A tightly stretched string with fixed end points x = 0 & x = ℓ is initially in the position y(x,0) = f(x). It is set vibrating by giving to each of its points a velocity ¶y/¶t = g(x) at t = 0 . Find the displacement y(x,t) in the form of Fourier series.
Solution
The displacement y(x,t) is given by the equation
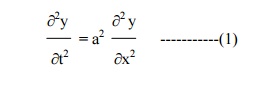
The boundary conditions are
(i) y(0,t) = 0, "t Âł0.
(ii) y(â„“,t) "t Âł=0. 0,
(iii) y(x,0) = f(x) , for 0 ÂŁx ÂŁâ„“.
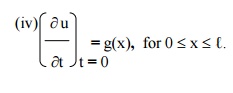
=g(x) , for 0 £x £ℓ. ¶t t
The solution of equation .(1) is given by
y(x,t) = (Acoslx + Bsinlx)(Ccoslat + Dsinlat) ------------(2)
where A, B, C, D are constants.
Applying conditions (i) and (ii) in (2), we have


Substituting the values of Bn and Dn in (3), we get the required solution of the given equation.
Exercises
(1) Find the solution of the equation of a vibrating string of length 'â„“', satisfying the conditions
y(0,t) = y(ℓ,t) = 0 and y = f(x), ¶y/ ¶t = 0 at t = 0.
(2) A taut string of length 20 cms. fastened at both ends is displaced from its position of equilibrium, by imparting to each of its points an initial velocity given by
v = x in 0 ÂŁx ÂŁ10
= 20 -x in 10 ÂŁx ÂŁ20,
„x‟ being the distance from one end. Determine the displacement at any subsequent time.
(3) Find the solution of the wave equation
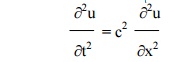
corresponding to the triangular initial deflection f(x ) = (2k/ â„“) x where 0<x<â„“/2
= (2k/ ℓ) –x)(ℓ-x) where ℓ/2<x<ℓ,
and initial velocity zero.
(4) A tightly stretched string with fixed end points x = 0 and x = ℓ is initially at rest in its equilibrium position. If it is set vibrating by giving to each of its points a velocity ¶y/ ¶t = f(x)
at t = 0. Find the displacement y(x,t).
(5) Solve the following boundary value problem of vibration of string
i. y(0,t) = 0
ii. y(â„“,t) = 0
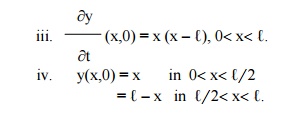
(6) A tightly stretched string with fixed end points x = 0 and x = ℓ is initially in a position given by y(x,0) = k( sin(px/ ℓ) – sin( 2px/ ℓ)). If it is released from rest, find the displacement of „y‟ at any distance „x‟ from one end at any time "t‟.
3 Solution of the heat equation
The heat equation is
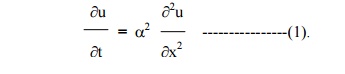
Let u = X(x) . T(t) be the solution of (1), where „X‟ is a function of „x‟ alone and „T‟ is a function of „t‟ alone.
Substituting these in (1), we get

Now the left side of (2) is a function of „x‟ alone and the right side is a function of „t‟ alone. Since „x‟ and „t‟ are independent variables, (2) can be true only if each side is equal to a constant.
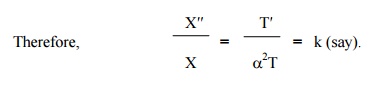
Hence, we get X′′ - kX = 0 and T′ -a2kT=0.-------------- (3).
Solving equations (3), we get
(i) when „k‟, is say positive and k =
X = c1 elx + c2 e - lx
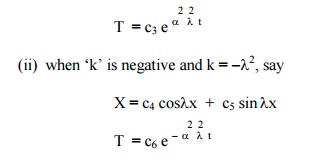
(iii) when „k‟ is zero.
X = c7 x + c8
T = c9
Thus the various possible solutions of the heat equation (1) are

Of these three solutions, we have to choose that solution which suits the physical nature of the problem and the given boundary conditions. As we are dealing with problems on heat flow, u(x,t) must be a transient solution such that „u‟ is to decrease with the increase of time „t‟.
Therefore, the solution given by (5),
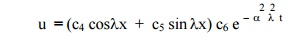
is the only suitable solution of the heat equation.
Illustrative Examples
Example 7
A rod „ℓ‟ cm with insulated lateral surface is initially at temperature f(x) at an inner point of distance x cm from one end. If both the ends are kept at zero temperature, find the temperature at any point of the rod at any subsequent time.

The boundary conditions are
(i)u (0,t) = 0, " t ≥ 0
(ii) u (â„“,t) "t > 0 = 0,
(iii) u (x,0) = f (x), 0 < x < â„“
The solution of equation (1) is given by


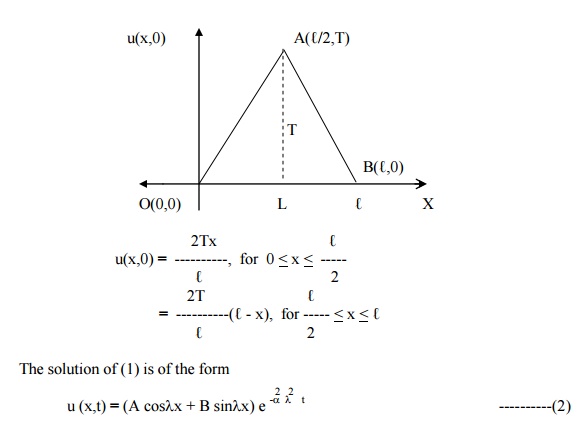
neglecting radiation. Find an expression for u, if the ends of the bar are maintained at zero temperature and if, initially, the temperature is T at the centre of the bar and falls uniformly to zero at its ends.

Let u be the temperature at P, at a distance x from the end A at time t.
The temperature function u (x,t) is given by the equation
The boundary conditions are
(i) u (0,t) = 0, "t > 0.
(ii) u (â„“=0,,t)"> 0.
The solution of (1) is of the form
Applying conditions (i) and (ii) in (2), we get

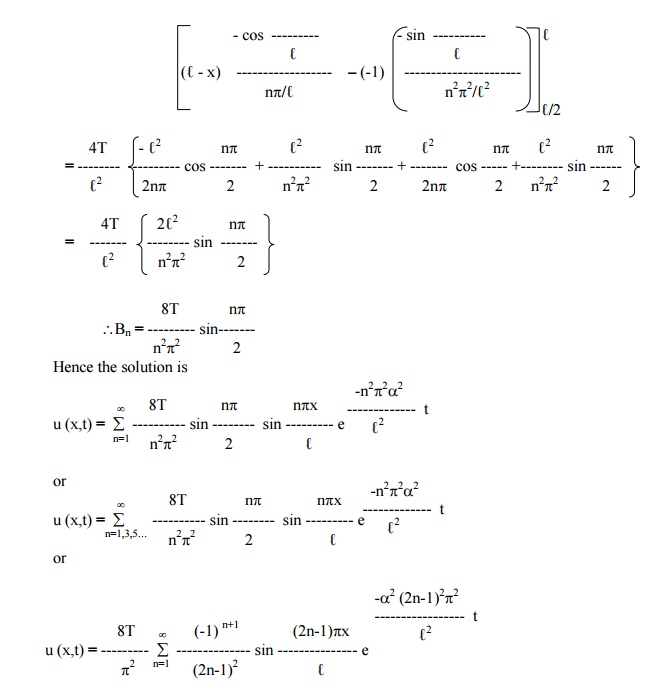
Steady - state conditions and zero boundary conditions Example 9
A rod of length „ℓ‟ has its ends A and B kept at 0°C and 100°C until steady state conditions prevails. If the temperature at B is reduced suddenly to 0°C and kept so while that of A is maintained, find the temperature u(x,t) at a distance x from A and at time „t‟.
The heat-equation is given by

Prior to the temperature change at the end B, when t = 0, the heat flow was independent of time (steady state condition).
When the temperature u depends only on x, equation(1) reduces to



Example 10
A rod, 30 c.m long, has its ends A and B kept at 20°C and 80°C respectively, until steady state conditions prevail. The temperature at each end is then suddenly reduced to 0°C and kept so. Find the resulting temperature function u (x,t) taking x = 0 at A.
The one dimensional heat flow equation is given by

The initial conditions, in steady –state, are
u = 20, when x = 0
u = 80, when x = 30
Therefore, (3) gives b = 20, a = 2.
u (x) = 2x + 20 ------------- (4)
Hence the boundary conditions are
(i) u (0,t) = 0, " t > 0
(ii) u (30,t) = 0, " t > 0
(iii) u (x,0) = 2x + 20, for 0 < x < 30
The solution of equation (1) is given by
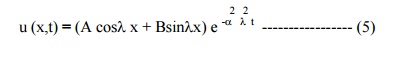
Applying conditions (i) and (ii), we get


Steady–state conditions and non–zero boundary conditions
Example 11
The ends A and B of a rod 30cm. long have their temperatures kept at 20°C and 80°C, until steady–state conditions prevail. The temperature of the end B is suddenly reduced to 60°C and kept so while the end A is raised to 40°C. Find the temperature distribution in the rod after time t.
Let the equation for the heat- flow be

The initial conditions, in steady–state, are
u = 20, when x = 0
u = 80, when x = 30
From (2), b = 20 & a = 2.
Thus the temperature function in steady–state is
u (x) = 2x + 20-------------- (3)
Hence the boundary conditions in the transient–state are
(i) u (0,t) = 40, " t > 0
(ii) u (30,t) = 60, " t > 0
(iii) u (x,0) = 2x + 20, for 0 < x < 30
we break up the required funciton u (x,t) into two parts and write
u (x,t) = us (x) + ut (x,t)--------------- (4)
where us (x) is a solution of (1), involving x only and satisfying the boundary condition (i) and (ii). ut (x,t) is then a function defined by (4) satisfying (1).
Thus us(x) is a steady state solution of (1) and ut(x,t) may therefore be regarded as a transient solution which decreases with increase of t.
To find us(x)
we have to solve the equation
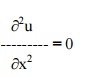
Solving, we get us(x) = ax + b ------------- (5)
Here us(0) = 40, us(30) = 60.
Using the above conditions, we get b = 40, a = 2/3.
To find ut(x,t)
ut ( x,t) = u (x,t) –us (x)
Now putting x = 0 and x = 30 in (4), we have
ut (0,t) = u (0,t) –us (0) = 40–40 = 0
and ut (30,t) = u (30,t) –us (30) = 60–60 = 0
Also ut (x,0) = u (x,0) –us (x)
Hence the boundary conditions relative to the transient solution ut (x,t) are
ut (0,t) = 0
ut (30,t) = 0 --------------(v)
and ut (x,0) = (4/3) x –20 ------------- (vi)


Exercises
(1) Solve ¶u/ ¶t = a2 (¶2u / ¶x2) subject to the boundary conditions u(0,t) = 0, u(l,t) = 0, u(x,0) = x, 0<x<l.
(2) Find the solution to the equation ¶u/ ¶t = a2 (¶2u / ¶x2) that satisfies the conditions
i. u(0,t) = 0,
ii. u(l,t) = 0, "t >0,
iii. u(x,0) = x for 0<x<l/ 2.
= l –x for l/ 2<x<l.
(3) Solve the equation ¶u/ ¶t = a2 (¶2u / ¶x2) subject to the boundary conditions
i. u(0,t) = 0,
ii. u(l,t) = 0, "t >0,
iii. u(x,0) = kx(l –x), k >0, 0 £x £l.
(4) A rod of length „l‟ has its ends A and B kept at 0 o C and 120 o C respectively until steady state conditions prevail. If the temperature at Bis reduced to 0 o C and kept so while that of A is maintained, find the temperature distribution in the rod.
(5) A rod of length „l‟ has its ends A and B kept at 0o C and 120 o C respectively until steady state conditions prevail. If the temperature at Bis reduced to 0 o C and kept so while 10 o C and at the same instant that at A is suddenly raised to 50 o C. Find the temperature distribution in the rod after time „t‟.
(6) A rod of length „l‟ has its ends A and B kept at 0 o C and 100 o C respectively until steady state conditions prevail. If the temperature of A is suddenly raised to 50 o C and that of B to 150 o C, find the temperature distribution at the point of the rod and at any time.
(7) A rod of length 10 cm. has the ends A and B kept at temperatures 30o C and 100o C, respectively until the steady state conditions prevail. After some time, the temperature at A is lowered to 20o C and that of B to 40o C, and then these temperatures are maintained. Find the subsequent temperature distribution.
(8) The two ends A and B of a rod of length 20 cm. have the temperature at 30o C and 80o C respectively until th steady state conditions prevail. Then the temperatures at the ends A and B are changed to 40o C and 60o C respectively. Find u(x,t).
(9) A bar 100 cm. long, with insulated sides has its ends kept at 0o C and 100o C until steady state condition prevail. The two ends are then suddenly insulated and kept so. Find the temperature distribution
(10) Solve the equation ¶u/ ¶t = a2 (¶2u / ¶x2) ) subject to the conditions (i) „u‟ is not infinite
as t ®¥ (ii) u = 0 for x = 0 and x = p, "t (iii) u = px -x2 for t = 0 in (0, p).
4 Solution of Laplace’s equation (Two dimensional heat equation)
The Laplace equation is
Let u = X(x) . Y(y) be the solution of (1), where „X‟ is a function of „x‟ alone and „Y‟ is a function of „y‟ alone.
Now the left side of (2) is a function of „x‟ alone and the right side is a function of „t‟ alone. Since „x‟ and „t‟ are independent variables, (2) can be true only if each side is equal to a constant.
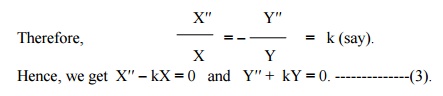
Solving equations (3), we get
(i) when „k‟ is positive and k = l2, say
X = c1 elx + c2 e - lx
Y = c3 cosly + c4 sin ly
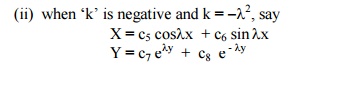
(iii) when „k‟ is zero.
X = c9 x + c10
Y = c11 x + c12
Thus the various possible solutions of (1) are
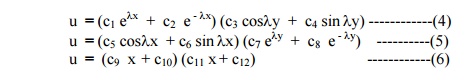
Of these three solutions, we have to choose that solution which suits the physical nature of the problem and the given boundary conditions.
Example 12
An infinitely long uniform plate is bounded by two parallel edges x = 0 & x = â„“ and an end at right angles to them. The breadth of this edge y = 0 is â„“ and this edge is maintained at a temperature f (x). All the other 3 edges are at temperature zero. Find the steady state temperature at any interior point of the plate.
Solution
Let u (x,y) be the temperature at any point x,y of the plate.
Also u (x,y) satisfies the equation


Using (7) in (5), we get the required solution.
Example 13
A rectangular plate with an insulated surface is 8 cm. wide and so long compared to its width that it may be considered as an infinite plate. If the temperature along short edge y = 0 is u(x,0) = 100 sin (px/8), 0 < x < 8, while two long edges x = 0 & x = 8 as well as the other short edges are kept at 0°C. Find the steady state temperature at any point of the plate.
Solution
The two dimensional heat equation is given by
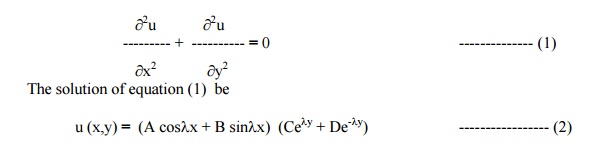
The boundary conditions are
(i) u (0, y) = 0, for 0 < y < ÂĄ
(ii) u (8, y) = 0, for 0 < y < ÂĄ
(iii) u (x, ÂĄ) = 0, for 0 < x < 8
(iv) u (x, 0) = 100 Sin (ÂĄx/8,) for 0 < x < 8
Using conditions (i), & (ii), we get

Comparing like coefficients on both sides, we get
D1 = 100, D2 = D3 = . . . . = 0
Substituting in (4), we get
u (x,y) = 100 e(-py / 8) sin (px / 8)
Example 14
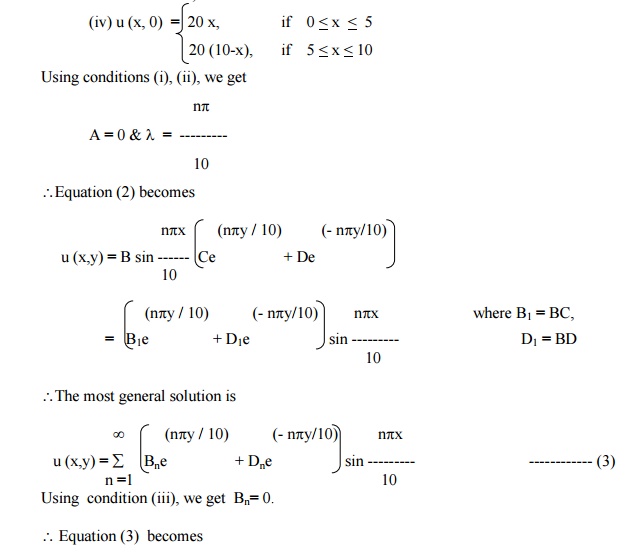
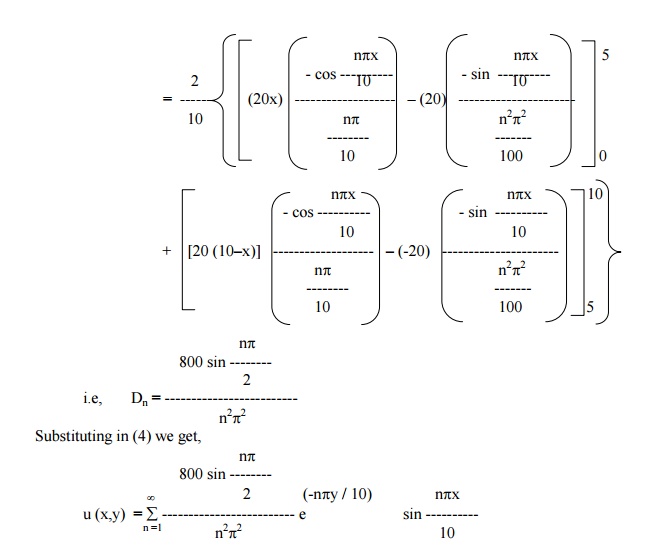
A rectangular plate with an insulated surface 10 c.m wide & so long compared to its width that it may considered as an infinite plate. If the temperature at the short edge y = 0 is given by
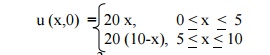
and all the other 3 edges are kept at temperature 0°C. Find the steady state temperature at any point of the plate.
Solution
The temperature function u (x,y) is given by the equation
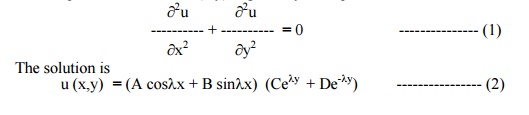
The boundary conditions are
(i) u (0, y) = 0, for 0 < y < ÂĄ
(ii) u (10, y) = 0, for 0 < y < ÂĄ
(iii) u (x, ÂĄ) = 0, for 0 < x < 10

Example 15
A rectangular plate is bounded by the lines x = 0, x = a, y = 0 & y = b. The edge temperatures are u (0,y) = 0, u (x,b) = 0, u (a,y) = 0 & u (x,0) = 5 sin (5px / a) + 3 sin (3px / a). Find the steady state temperature distribution at any point of the plate.
The temperature function u (x,y) satisfies the equation
The boundary conditions are
(i) u (0,y) = 0, for 0 < y < b
(ii) u (a,y) = 0, for 0 < y < b
(iii) u (x, b) = 0, for 0 < x < a
(iv) u (x,0) = 5 sin (5px / a) + 3 sin (3px / a), for 0 < x < a.



Exercises
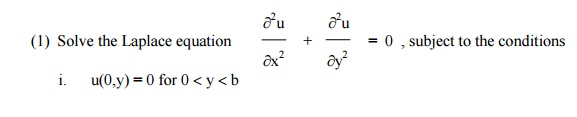
ii. u(a,y) = 0 for 0 <y <b
iii. u(x,b) = 0 for 0 <x <a
iv. u(x,0) = sin3(px/ a) ,0 <x <a.
(2) Find the steady temperature distribution at points in a rectangular plate with insulated faces and the edges of the plate being the lines x = 0, x = a, y = 0 and y = b. When three of the edges are kept at temperature zero and the fourth at a fixed temperature ao C.

i. u(0,y) = 0, 0 ÂŁy ÂŁl ii. u(l,y) = 0, 0 ÂŁy ÂŁl
iii. u(x,0) = 0, 0 ÂŁx ÂŁl iv. u(x,l) = f(x), 0 ÂŁx ÂŁl
(6) A square plate is bounded by the lines x = 0, y = 0, x = 20 and y = 20. Its faces are insulated.
The temperature along the upper horizontal edge is given by u(x,0) = x (20 –x), when 0 < x <20,
while other three edges are kept at 0o C. Find the steady state temperature in the plate.
(7) An infinite long plate is bounded plate by two parallel edges and an end at right
angles to them.The breadth is p. This end is maintained0‟atat a c all points and the other edges are at zero temperature. Find the steady state temperature at
any point (x,y) of the plate.
(8) An infinitely long uniform plate is bounded by two parallel edges x = 0 and x = l, and
an end at right angles to them. The breadth of this edge y = 0 is „l‟ and temperature f(x). All the other three edges are at temperature zero. Find the steady state
temperature at any interior point of the plate.
(9) A rectangular plate with insulated surface is 8 cm. wide and so long compared to its width that it may be considered infinite in length without introducing an appreciable error. If the temperature along one short edge y = 0 is given by u(x,0) = 100 sin(px/ 8), 0 <x <8, while the two long edges x = 0 and x = 8 as well as the other short edge are kept at 0o C, show that the steady state temperature at any point of the plane is given by u(x,y) = 100 e-py/ 8 sin px/ 8 .
(10) A rectangular plate with insulated surface is 10 cm. wide and so long compared to its width that it may be considered infinite length. If the temperature along short edge y = 0 is given
u(x,0) = 8 sin(px/ 10) when 0 <x <10, while the two long edges x = 0 and x = 10 as well as the other short edge are kept at 0o C, find the steady state temperature distribution u(x,y).
Related Topics