Solution of the heat equation

Solution of the heat equation

The heat equation is

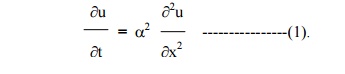
Let u = X(x) . T(t) be the solution of (1), where „X‟ is a function of „x‟ alone and „T‟ is a function of „t‟ alone.

Substituting these in (1), we get

Now the left side of (2) is a function of „x‟ alone and the right side is a function of „t‟  alone. Since „x‟ and „t‟ are independent variables, (2) can be true only if each side is  equal to a constant.  

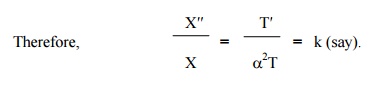
Hence, we get X′′ - kX = 0 and T′ -a2kT=0.-------------- (3).

Solving equations (3), we get

(i)                                when   â€žk‟, is say   positive   and   k   = l2

X = c1 elx  + c2  e - lx

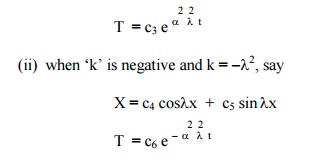
(iii)     when   â€žk‟   is   zero.     

X = c7 x + c8       

T = c9                   

Thus the various possible solutions of the heat equation (1) are

Of these three solutions, we have to choose that solution which suits the physical nature of the problem and the given boundary conditions. As we are dealing with problems on heat flow, u(x,t) must be a transient solution such that „u‟ is to decrease with the increase of time „t‟.

Therefore, the solution given by (5),

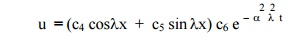
is the only suitable solution of the heat equation.

Illustrative Examples

Example 7

A rod „ℓ‟ cm with insulated lateral surface is initially at temperature f(x) at an inner point of distance x cm from one end. If both the ends are kept at zero temperature, find the temperature at any point of the rod at any subsequent time.

The boundary conditions are                             

(i)u (0,t) = 0,      " t   â‰¥   0              

(ii)   u   (â„“,t) "t > 0 =   0, 

(iii)  u   (x,0)   =   f   (x),   0   <   x   <   â„“ 

The solution of equation (1) is given by

neglecting radiation. Find an expression for u, if the ends of the bar are maintained at zero temperature and if, initially, the temperature is T at the centre of the bar and falls uniformly to zero at its ends.

Let u be the temperature at P, at a distance x from the end A at time t.

The temperature function u (x,t) is given by the equation

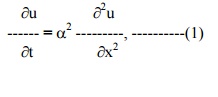
The boundary conditions are

(i)                u (0,t)  = 0, "t > 0. 

(ii)             u   (â„“=0,,t)"> 0. 

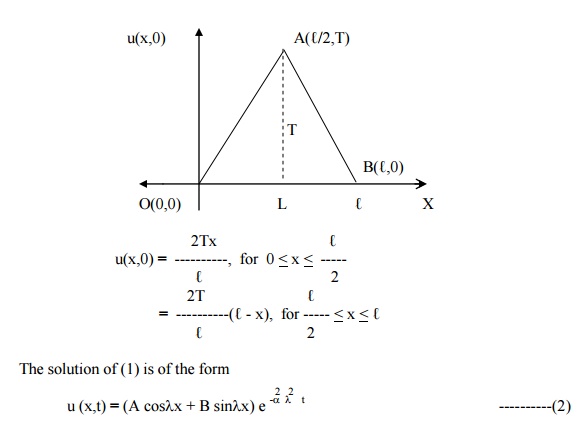
The solution of (1) is of the form

Applying conditions (i) and (ii) in (2), we get

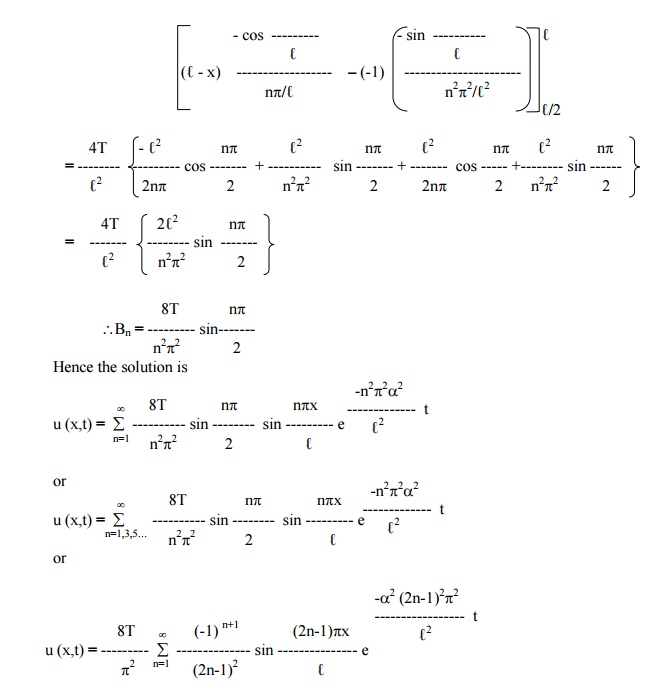
Steady - state conditions and zero boundary conditions Example 9

A rod of length „ℓ‟ has its ends A and B kept at 0°C and 100°C until steady state   conditions prevails. If the temperature at B is reduced suddenly to 0°C and kept so while that of A is maintained, find the temperature u(x,t) at a distance x from A and at time „t‟.  

The heat-equation is given by

Prior to the temperature change at the end B, when t = 0, the heat flow was independent of time (steady state condition).  

When the temperature u depends only on x, equation(1) reduces to 

Example 10

A rod, 30 c.m long, has its ends A and B kept at 20°C and 80°C respectively, until steady state conditions prevail. The temperature at each end is then suddenly reduced to 0°C and kept so. Find the resulting temperature function u (x,t) taking x = 0 at A.

The one dimensional heat flow equation is given by

The initial conditions, in steady –state, are

          u = 20, when        x = 0

          u = 80, when        x = 30         

Therefore, (3) gives b = 20, a = 2.     

          u (x) = 2x + 20     ------------- (4)

Hence the boundary conditions are   

(i)      u (0,t) = 0,  " t > 0        

(ii)     u (30,t) = 0, " t > 0        

(iii)    u (x,0)         = 2x + 20, for 0 < x < 30

The solution of equation (1) is given by     

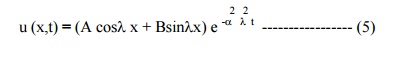
Applying conditions (i) and (ii), we get

Steady–state conditions and non–zero boundary conditions

Example 11

The ends A and B of a rod 30cm. long have their temperatures kept at 20°C and 80°C, until steady–state conditions prevail. The temperature of the end B is suddenly reduced to 60°C and kept so while the end A is raised to 40°C. Find the temperature distribution in the rod after time t.

Let the equation for the heat- flow be

The initial conditions, in steady–state, are           

u = 20,        when x =  0          

u = 80,        when x = 30                   

From (2), b = 20  & a = 2.

Thus the temperature function in steady–state is

          u (x) = 2x + 20--------------       (3)

Hence the boundary conditions in the transient–state are       

(i)      u (0,t) = 40, " t > 0        

(ii)     u (30,t) = 60,        " t > 0        

(iii)    u (x,0) = 2x + 20, for 0 < x < 30 

we break up the required funciton u (x,t) into two parts and write

u (x,t) = us (x) + ut (x,t)--------------- (4)

where us (x) is a solution of (1), involving x only and satisfying the boundary condition (i) and (ii). ut (x,t) is then a function defined by (4) satisfying (1).

Thus us(x) is a steady state solution of (1) and ut(x,t) may therefore be regarded as a transient solution which decreases with increase of t.

To find us(x)

we have to solve the equation

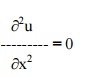
Solving, we get us(x) = ax + b           ------------- (5)

Here us(0) = 40, us(30) = 60.

Using the above conditions, we get b = 40, a = 2/3.

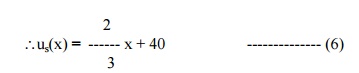
To find ut(x,t)

ut ( x,t) = u (x,t) –us (x)

Now putting x = 0 and x = 30 in (4), we have

ut (0,t) = u (0,t)  â€“us (0) =         40–40 = 0

and   ut (30,t) = u (30,t) –us (30) = 60–60 = 0

Also ut (x,0) = u (x,0) –us (x)

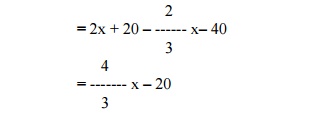
Hence the boundary conditions relative to the transient solution ut (x,t) are

ut (0,t)  = 0  

ut (30,t) = 0  --------------(v)

and ut (x,0) = (4/3) x –20 ------------- (vi)

Exercises

(1) Solve Â¶u/ Â¶t = a2 (¶2u / Â¶x2) subject to the boundary conditions u(0,t) = 0, u(l,t) = 0, u(x,0) = x, 0<x<l. 

(2)     Find the solution to the equation  Â¶u/ Â¶t = a2 (¶2u / Â¶x2) that satisfies the conditions 

i.           u(0,t) = 0, 

ii.           u(l,t) = 0, "t >0,

iii.    u(x,0) = x  for 0<x<l/ 2.

=    l –x  for l/ 2<x<l.

(3)   Solve the equation  Â¶u/ Â¶t = a2 (¶2u / Â¶x2) subject to the boundary conditions 

i.           u(0,t) = 0, 

ii.           u(l,t) = 0, "t >0,

iii.           u(x,0) = kx(l –x), k >0, 0 Â£x Â£l. 

 (4) A rod of length „l‟ has its ends A and B kept at 0 o  C and 120 o   C respectively until steady state conditions prevail. If the temperature at Bis reduced to 0 o  C and kept so while that of A is maintained, find the temperature distribution in the rod.

(5) A rod of length „l‟ has its ends A and B kept at 0o C and 120 o  C respectively until steady state conditions prevail. If the temperature at Bis reduced to 0 o  C and kept so while 10 o  C and at the same instant that at A is suddenly raised to 50 o  C. Find the temperature distribution in the rod after time „t‟.

 (6) A rod of length „l‟ has its ends A and B kept at 0 o  C and 100 o  C respectively until steady state conditions prevail. If the temperature of A is suddenly raised to 50 o  C and that of B to 150 o  C, find the temperature distribution at the point of the rod and at any time.

(7)   A rod of length 10 cm. has the ends A and B kept at temperatures 30o C and 100o C, respectively until the steady state conditions prevail. After some time, the temperature at A is lowered to 20o C and that of B to 40o C, and then these temperatures are maintained. Find the subsequent temperature distribution. 

(8)   The two ends A and B of a rod of length 20 cm. have the temperature at 30o C and 80o C respectively until th steady state conditions prevail. Then the temperatures at the ends A and B are changed to 40o C and 60o C respectively. Find u(x,t). 

(9)   A bar 100 cm. long, with insulated sides has its ends kept at 0o C and 100o C until steady state condition prevail. The two ends are then suddenly insulated and kept so. Find the temperature distribution