Important Questions and Answers: Applications of Partial Differential Equations

APPLICATIONS OF PARTIAL DIFFERENTIAL EQUATIONS

PART –A

1. What conditions are assumed in deriving the one dimensional wave equation?

The wave equation is

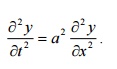
In deriving this equation we make the following assumptions.

(i)    The motion takes place entirely in one plane i.e., XY plane.

(ii) We  consider  only  transverse  vibrations  the  horizontal  displacement  of  the

particles of the string is negligible.

(iii)The tension T is constant at all times and at all points of the deflected string.

(iv)                       T is considered to be so large compared with the weight of the string and hence the force of gravity is negligible.

(v) The effect of friction is negligible.

(vi)                       The string is perfectly flexible.

2.State the wave equation and give the various solutions of it?

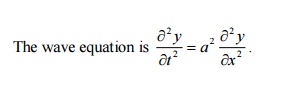
The various possible solutions of this equation are

(i)      y(x,t) =( A₁e ^px +A₂ e^-px )( A₃e ^pat +A₄ e^-pat ) .

(ii)   y(x,t) =( A₅ cos px +A₆ sin px)( A₇ cos pat +A₈ sin pat)

(iii) y(x, t) =( A₉ x +A₁₀ )( A₁₁t +A₁₂ ) .

3. Find the nature of PDE

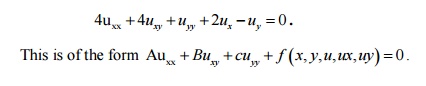
Here A =4, B  =4,C=.1

B²-4AC=16-4(4)(1)=0.

Therefore the equation is Parabolic.

Classify the equation u_xx-y⁴u_yy=2y³u_y. Solution:

This is of the form Au_xx+Buxy+Cu_yy+f(x,y,u,u_x,u_y)=0.

Here A=1, B=0, C=-1.

B²-4AC=0-4(1)(-1)=4>0.

Therefore the equation is Hyperbolic.

2.     Classify: x²uxx+2xyu_xy+(1+y²) u_yy-2u_x=0. Solution:

This is of the form Au_xx+Buxy+Cu_yy+f(x,y,u,u_x,u_y)=0.

Here A=x², B=2xy, C=1+y².

B²-4AC=4x²y²-4(x²)(1+y²)

= 4x²y²-4 x²-4(x² y²)

=-4x²<0.

Therefore the equation is Elliptic.

3.  A  string  is stretched  and  fastened  to  two point  l  apart. Motion is started  by

displacing the string into the form  y =y⁰ sin px/ l from  which it is released at time t=0. Formulate this problem as the boundary value problem. Solution:

The displacement y(x,t) is the solution of the wave equation.

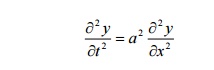
The boundary conditions are:

4.  What is the constant a² in the wave equation

Solution:

u(x, t) =( Acos px +B sin px)e^{-c2 p2t} .

6.     State the governing equation for one dimensional heat equation and necessary conditions to solve the problem.

Solution:

temperature at time t at a point distance x from the left end of the rod.

The boundary conditions are

i)                   u(0, t) =k ⁰₁C for all t ³0

ii)                u(l, t) =k ⁰₂C for all t ³0

iii)              the initial condition is u(x,0) =f (x), 0 <x <l .

7.Write all variable separable solutions of the one dimensional heat equation

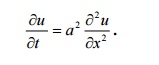
Solution:

i)   u(x, t) =( A₁e^lx  +B₂ e^-lx )C₁e^a2l2t

ii)u(x,t) =( A₂ cos lx +B₂ sin lx) C₂ e^-a2l2t

iii)  u(x, t) =( A₃ x +B₃ )C₃ .

8.     Write down the diffusion problem in one dimension as a boundary value problem in two different forms.

Solution:

9.     State any two laws which are assumed to derive one dimensional heat equation. Solution:

i)                   Heat flows from higher to lower temperature

ii)                The rate at which the heat flows across any area is proportional to the area and to the temperature gradient normal to the curve. This constant is proportionality is known as the thermal conductivity (k) of the material. It is known as Fourier law of heat conduction.

10.            Write any two solutions of the Laplace equation U_xx+U_yy=0 involving exponential terms in x or y.

Solution:

i)   u(x, y) =( A₁e ^px +A₂ e^-px )( A₃ cos py +A₄ sin py ) .

ii)  u(x, y) =( A₁ cos px +A₂ sin px)( A₃e ^py  +A₄ e^-py ) .

11.            In steady state conditions derive the solution of one dimensional heat flow equation. Solution:

The PDE of unsteady one dimensional heat flow is

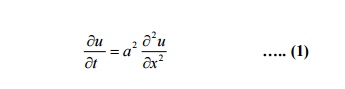
In steady state condition, the temperature u depends only on x and not on t.

The general solution is u=ax+b, where a, b are arbitary.

12.            Write the boundary condition and initial conditions for solving the vibration of string equation, if the string is subjected to initial displacement f(x) and initial velocity g(x).

Solution:

The initial and boundary conditions are

i)   y(0, t) =0 .

ii)    y(l, t) =0 .

iii)      ^¶y (x,0)=g(x) .

¶t

iv)  y(x,0) =f (x)

Write down the governing equation of two dimensional steady state heat equation. Solution:

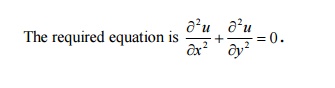
14.            The ends A and B of a rod of length 10cm long have their temperature distribution kept at 20^oC and 70^oC. Find the steady state temperature distribution of the rod. Solution:

The steady state equation of one dimensional heat flow is

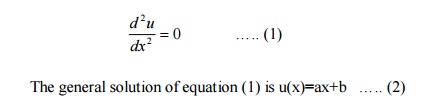
The boundary conditions are u(0)=20, u(l)=70. 

Put x=0 in (2) we get u(0)=a(0)+b

Þb=20 

Put x=l in (2) we get u(l)=al+b

70= al+20 al=50

a= 50/l

Therefore equation (2) Þ u(x)= 50x/l+20

Here l=10 cm

Therefore u(x)= 50x/10+20 u(x)=5x+20.

15.                        Write down the different solutions of Laplace equation in polar coordinates.

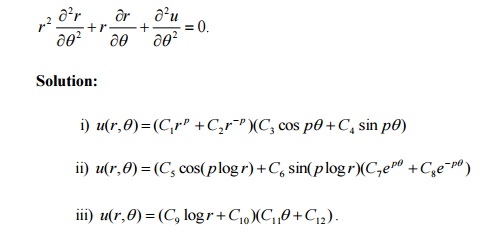
i) u(r,q) =(C₁r ^p  +C₂ r ^-p )(C₃ cos pq+C₄ sin pq)

ii)  u(r,q) =(C₅ cos( p log r) +C₆ sin( p log r)(C₇ e ^pq +C₈e^-pq)

iii)  u(r,q) =(C₉ log r +C₁₀ )(C₁₁q+C₁₂ ) .

16.                        What is the general solution of a string of length l whose end points are fixed and which starts from rest?

Solution:

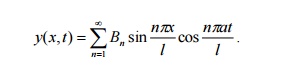
17.                        How many boundary conditions and initial conditions are required to solve the one dimensional wave equation?

Solution:

Two boundary conditions and two initial conditions are required.

PART B

1.A string is stretched and fastened to two points x = 0 and x= l apart. Motion is started by displacing the string into the form y = k (l x –x² ) from which it is released at time t=0. Find the displacement of any point on the sting at a distance of x from one end at time t.

Solution:  The ODWE             y_tt=c 2 y_cc

Solution :  y(x,t)= (Acos px +Bsin px)(Ccos pct +Dsin pct)

Boundary and initial conditions are (i) y(0,t) = 0 (ii) y(l,t) = 0

(iii) y _t (x,0)=0 (iv) y(x,0)=f(x), 0< x < l .

Using Boundary and initial conditions:

i)                             y(0,t) = 0, put x=0

A(Ccos pct +Dsin pct)=0  \ A=0

\ Suitable solution y(x,t)= Bsin px (Ccos pct +Dsin pct)

ii)              y(l,t) = 0 , put x=l

Bsin pl (Ccos pct +Dsin pct)=0 ÞB ¹0 Bsin pl =0

2.A taut string of length 2l is fastened at both ends . The midpoint of the string is taken to a height b and then released from rest in that position. Find the displacement of the string at any time.

Solution: let L=2l

Suitable solution y(x,t)= (Acos px +Bsin px)(Ccos pct +Dsin pct)

Boundary and initial conditions are

(i) y(0,t) = 0 (ii) y(l,t) = 0 (iii) y _t (x,0)=0 (iv) y(x,0)=f(x), 0< x < l .

Using Boundary and initial conditions:

i)  y(0,t) = 0, put x=0

A(Ccos pct +Dsin pct)=0 \ A=0

Suitable solution y(x,t)= Bsin px (Ccos pct +Dsin pct)

ii)  y(l,t) = 0 , put x=l

Bsin pl (Ccos pct +Dsin pct)=0 ÞB ¹0 Bsin pl =0

3.If a string of length  ' l ' is initially at rest in its equilibrium position and each of its points

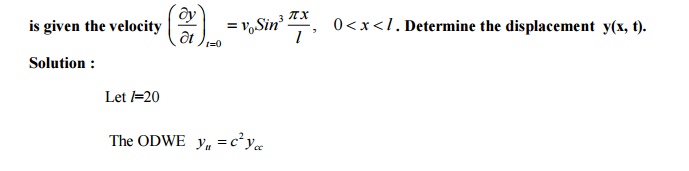
Suitable solution y(x,t)= (Acos px +Bsin px)(Ccos pct +Dsin pct)

Boundary and initial conditions are (i) y(0,t) = 0 (ii) y(l,t) = 0

(iii) y (x,0)=0 (iv) y t (x,0)=f(x) =v0 sin^{3 px} / l

Using Boundary and initial conditions:

i)  y(0,t) = 0, put x=0

A(Ccos pct +Dsin pct)=0  \ A=0

\ Suitable solution y(x,t)= Bsin px (Ccos pct +Dsin pct)

ii)  y(l,t) = 0 , put x=l

Bsin pl (Ccos pct +Dsin pct)=0 ÞB ¹0 Bsin pl =0

4.A rod 30 cm long has its ends A and B kept at 20⁰C and 80⁰C respectively until steady state conditions prevail the temperature at each end is then suddenly reduced to 0⁰ c and kept so. Find the resulting temperature function u(x,t) taking x=0 at A.

Solution:

After change  ODHE: u_t  =a²u_xx

Suitable Solutions:

u(x,t)= (Acospx + Bsin px) e^{-a2 p2t}

Boundary and Initial Conditions:

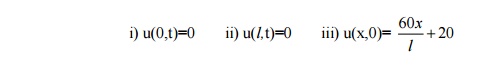
Using Boundary and initial conditions:

i)       u(0,t)=0

Here x=0 Þ u(0,t)= Ae ^{-a2 p2t}

\A=0

5. An infinitely long rectangular plate with insulated surface 10 cm wide. The two long edges and one short edge are kept at 0⁰ temperature, while the other short edge x=0 is kept at temperature given by u=20y, 0 £y £5, u=20(10-y),5 £y £10. Find the steady state temperature in the plate.

Solution : Steady state two dimensional heat equation:

u_xx +u_yy  =0

Infinite plate extended in x-direction :        Let l=10

I Boundary Conditions

i) u(x,0) = 0   ii) u(x,l) = 0

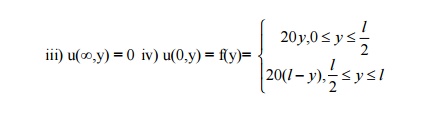
II Suitable Solution:

u(x,y)= (Ae ^-px +Be ^px )(Ccospy + Dsinpy)

Using boundary conditions:

u(x,0) = (Ae^-px +Be ^px )C =0

C=0

Suitable Solution:

u(x,y)= (Ae ^-px +Be ^px )Dsinpy

ii)  u(x,l) = 0