Chapter: Mathematics (maths) : Applications of Partial Differential Equations
Solution of the wave equation
Solution of the wave equation
The wave equation is
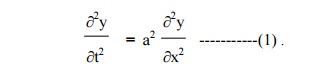
Let y = X(x) . T(t) be the solution of (1), where „X‟ is a function of „x‟ only and „T‟ is a function of „t‟ only.
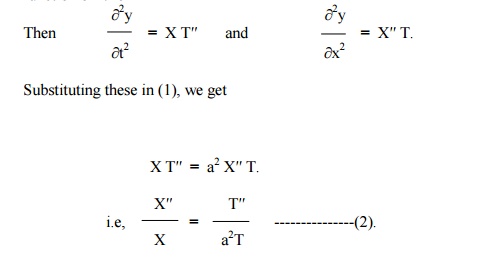
Of these three solutions, we have to select that particular solution which suits the physical nature of the problem and the given boundary conditions. Since we are dealing with problems on vibrations of strings, „y‟ must be a periodic function of „x‟ and „t‟.

Now the left side of (2) is a function of „x‟ only and the right side is a function of „t‟ only.
Since „x‟ and „t‟ are independent variables, (2) can hold good only if each side is equal to a constant.
Hence the solution must involve trigonometric terms.
Therefore, the solution given by (5),
i.e, y = (c5 coslx + c6 sin lx) (c7 cosalt+ c8 sin alt)
is the only suitable solution of the wave equation.
llustrative Examples.
Example 1
If a string of length ‚Ñì is initially at rest in equilibrium position and each of its points is given the velocity
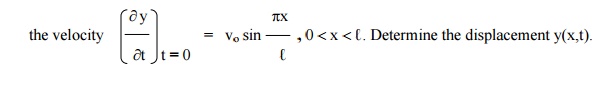
Solution
The displacement y(x,t) is given by the equation
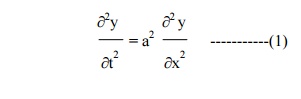
The boundary conditions are
i. y(0,t) = 0, for t ³0.
ii. y(ℓ,t) ³0.= 0, for t
y(x,0) = 0, for 0 £x £ℓ.
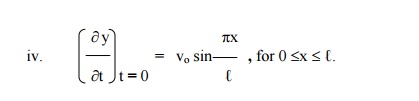
Since the vibration of a string is periodic, therefore, the solution of (1) is of the form
y(x,t) = (Acoslx + Bsinlx)(Ccoslat + Dsinlat) ------------(2)
Using (i) in (2) , we get
0 = A(Ccoslat + Dsinlat) , for all t ³0.
Therefore, A = 0
Hence equation (2) becomes
y(x,t) = B sinlx(Ccoslat + Dsinlat) ------------ (3)
Using (ii) in (3), we get
0 = Bsinlℓ (Ccoslat+Dsinlat), for all t ³0, which gives lℓ = n
Hence, l= np / l , n being an integer.

Using condition (iv) in the above equation, we get

Example 2
A tightly stretched string with fixed end points x = 0 & x = ‚Ñì is initially at rest in its equilibrium position . If it is set vibrating by giving to each of its points a velocity
¶y/¶t = kx(ℓ-x) at t = 0. Find the displacement y(x,t).
Solution
The displacement y(x,t) is given by the equation
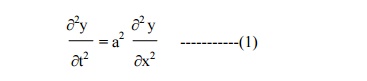
The boundary conditions are


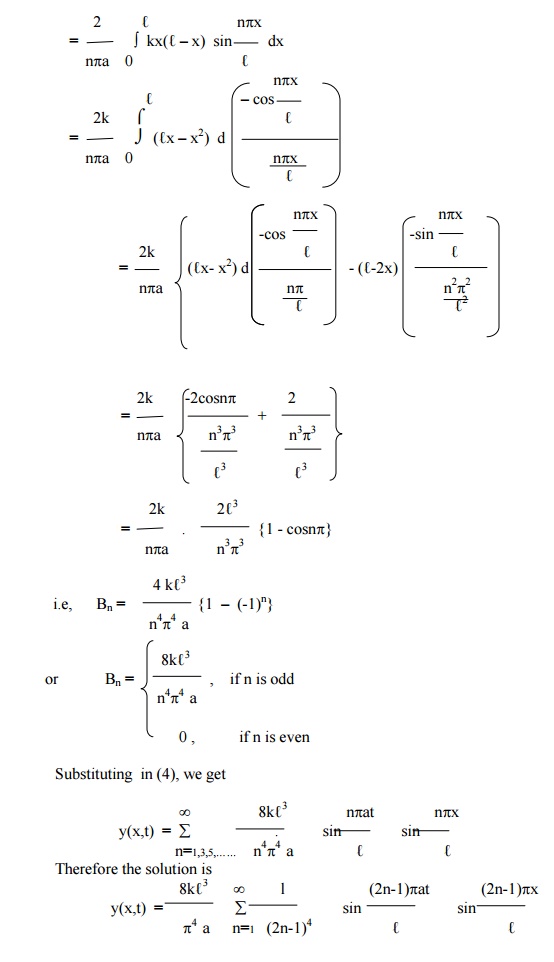
Example 3
A tightly stretched string with fixed end points x = 0 & x = ‚Ñì is initially in a position given by y(x,0) = y0sin3(px/‚Ñì). If it is released from this position, find the displacement y at any time and at any distance from the end x = 0 .
Solution
The displacement y(x,t) is given by the equation
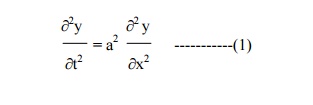
The boundary conditions are
(i) y(0,t) = 0, "t ³0.
(ii) y("tℓ³,t)0. = 0,
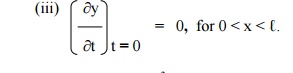
(iv) y(x,0) = y0 sin3((px/‚Ñì), for 0 < x < ‚Ñì.
The suitable solution of (1) is given by
y(x,t) = (Acoslx + Bsinlx)(Ccoslat + Dsinlat) ------------(2)
Using (i) and (ii) in (2) , we get


Example 4
A string is stretched & fastened to two points x = 0 and x = ‚Ñì apart. Motion is started by displacing the string into the form y(x,0) = k(‚Ñìx-x2) from which it is released at time t = 0. Find the displacement y(x,t).
Solution
The displacement y(x,t) is given by the equation
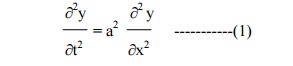
The boundary conditions are
(i) y(0,t) = 0, "t ³0.
(ii) y(ℓ,t) "t ³=0. 0,
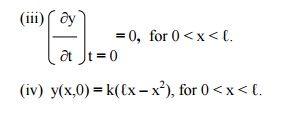
The suitable solution of (1) is given by
y(x,t) = (Acoslx + Bsinlx)(Ccoslat + Dsinlat) ------------(2)
Using (i) and (ii) in (2) , we get

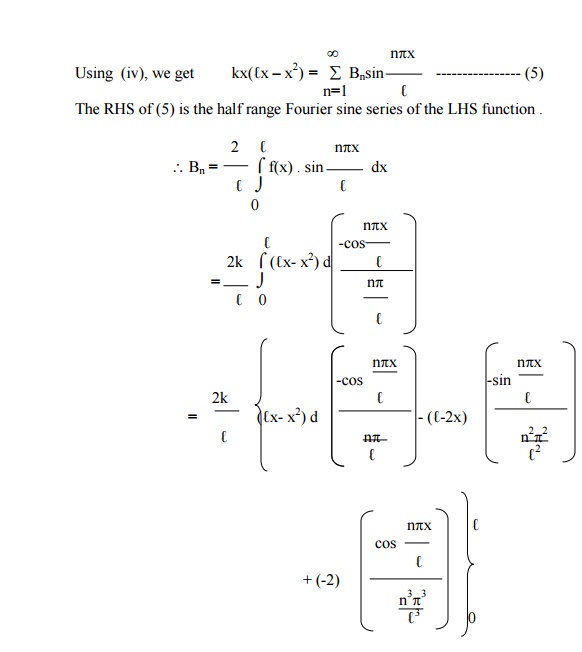

Example 5
Solution
The displacement y(x,t) is given by the equation
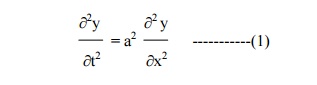
The suitable solution of (1) is given by
y(x,t) = (Acoslx + Bsinlx)(Ccoslat + Dsinlat) ------------(2)
The boundary conditions are
(i) y(0,t) = 0, "t ³0.
(ii) y(ℓ,t) "t ³=0. 0,
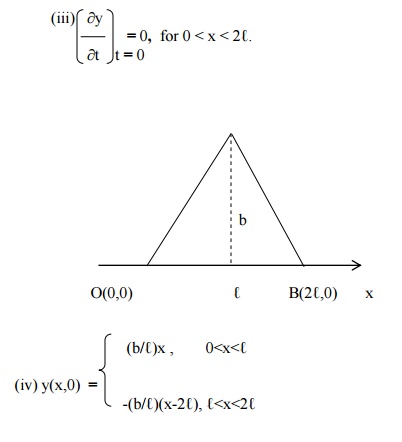
[Since, equation of OA is(y- b)/(oy-b)== (x(b/-‚Ñì)/(2‚Ñì-‚Ñì)x)]‚Ñì
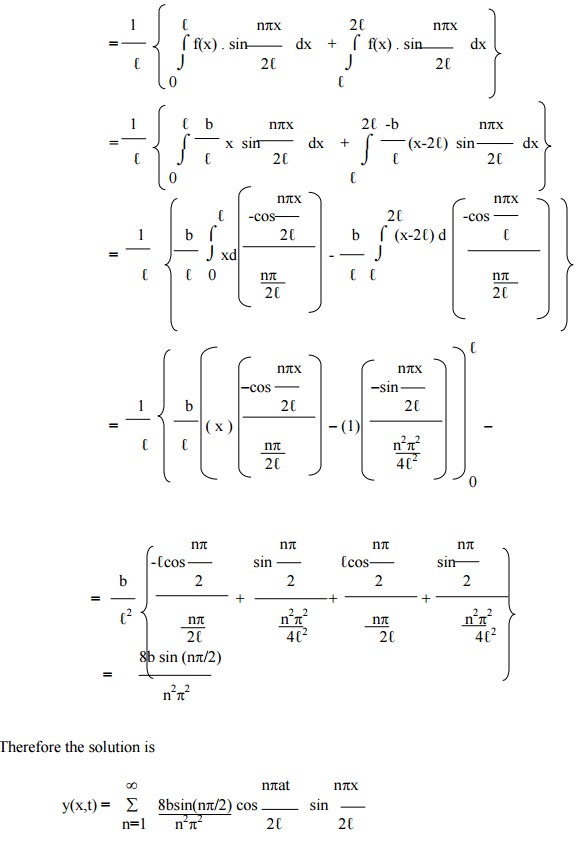
Using conditions (i) and (ii) in (2), we get

Here B can not be zero, therefore D = 0.
Hence equation (3) becomes

Example 6
A tightly stretched string with fixed end points x = 0 & x = ℓ is initially in the position y(x,0) = f(x). It is set vibrating by giving to each of its points a velocity ¶y/¶t = g(x) at t = 0 . Find the displacement y(x,t) in the form of Fourier series.
Solution
The displacement y(x,t) is given by the equation
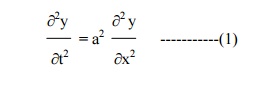
The boundary conditions are
(i) y(0,t) = 0, "t ³0.
(ii) y(ℓ,t) "t ³=0. 0,
(iii) y(x,0) = f(x) , for 0 £x £ℓ.
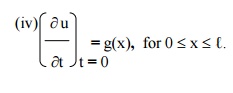
=g(x) , for 0 £x £ℓ. ¶t t
The solution of equation .(1) is given by
y(x,t) = (Acoslx + Bsinlx)(Ccoslat + Dsinlat) ------------(2)
where A, B, C, D are constants.
Applying conditions (i) and (ii) in (2), we have


Substituting the values of Bn and Dn in (3), we get the required solution of the given equation.
Exercises
(1) Find the solution of the equation of a vibrating string of length '‚Ñì', satisfying the conditions
y(0,t) = y(ℓ,t) = 0 and y = f(x), ¶y/ ¶t = 0 at t = 0.
(2) A taut string of length 20 cms. fastened at both ends is displaced from its position of equilibrium, by imparting to each of its points an initial velocity given by
v = x in 0 £x £10
= 20 -x in 10 £x £20,
„x‟ being the distance from one end. Determine the displacement at any subsequent time.
(3) Find the solution of the wave equation
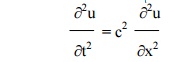
corresponding to the triangular initial deflection f(x ) = (2k/ ‚Ñì) x where 0<x<‚Ñì/2
= (2k/ ℓ) –x)(ℓ-x) where ℓ/2<x<ℓ,
and initial velocity zero.
(4) A tightly stretched string with fixed end points x = 0 and x = ℓ is initially at rest in its equilibrium position. If it is set vibrating by giving to each of its points a velocity ¶y/ ¶t = f(x)
at t = 0. Find the displacement y(x,t).
(5) Solve the following boundary value problem of vibration of string
i. y(0,t) = 0
ii. y(‚Ñì,t) = 0
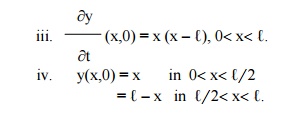
(6) A tightly stretched string with fixed end points x = 0 and x = ℓ is initially in a position given by y(x,0) = k( sin(px/ ℓ) – sin( 2px/ ℓ)). If it is released from rest, find the displacement of „y‟ at any distance „x‟ from one end at any time "t‟.
Related Topics