Parseval’s Theorem and Change of Interval

Parseval’s Theorem 

Root Mean square value of the function f(x) over an interval (a, b) is defined as

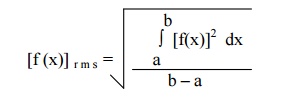
The use  of r.m.s value of a periodic  function is frequently made in the theory of mechanical vibrations and in electric circuit theory. The r.m.s value  is known as the effective value of the  function.

Parseval’s   Theorem

If f(x) defined in the interval (c, c+2Ï€ ), then the Parseval‟s Identity is given by 

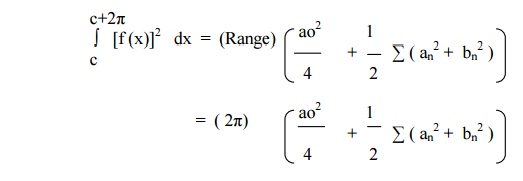
Example 13

Obtain the Fourier series for f(x) 

CHANGE OF INTERVAL

In most of the Engineering applications, we require an expansion of a given function over an interval 2l other than 2p.

Suppose f(x) is a function defined in the interval c< x < c+2l. The Fourier expansion for f(x) in the interval c<x<c+2l is given by

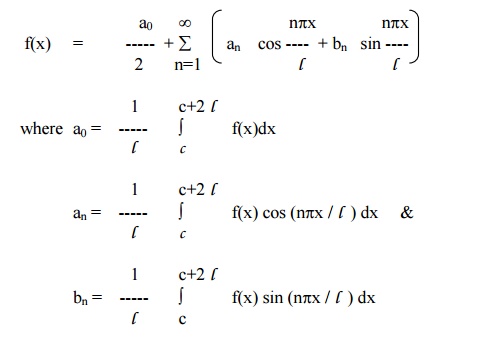
Even and Odd Function

If f(x) is an even function and is defined in the interval ( c, c+2 l ), then 

Half Range Series

Sine Series

Cosine series

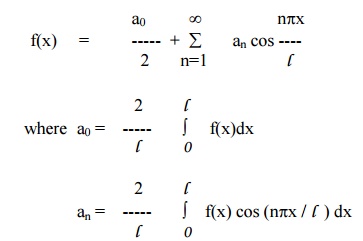
Example 14

Find the Fourier series expansion for the function

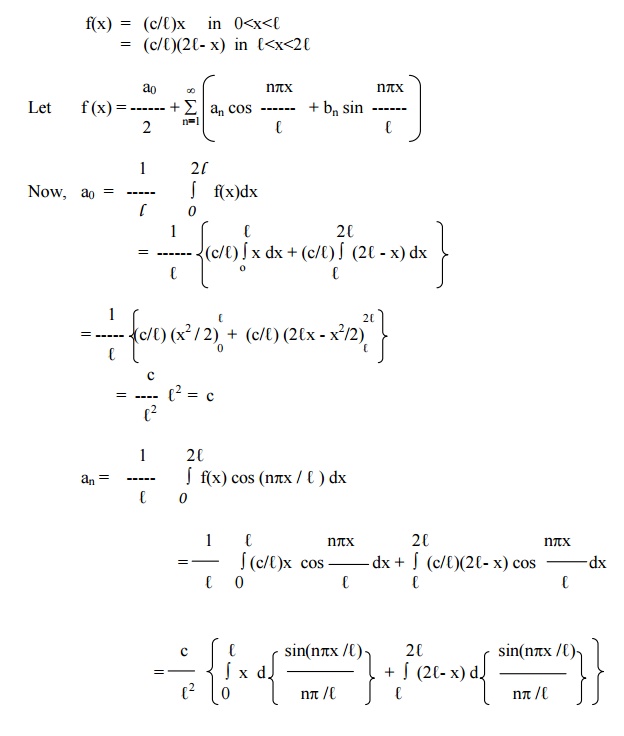
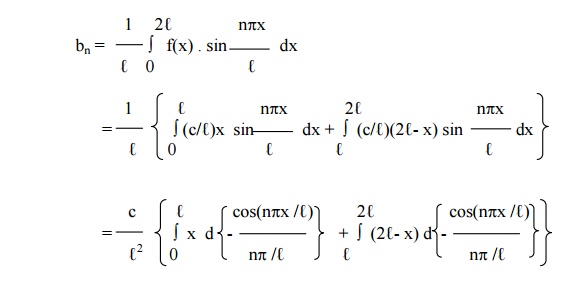
Example 15

Find the Fourier series of periodicity 3 for f(x) = 2x –x2 , in 0 <x <3.

Here 2â„“ = 3. 

\ â„“ = 3 / 2.

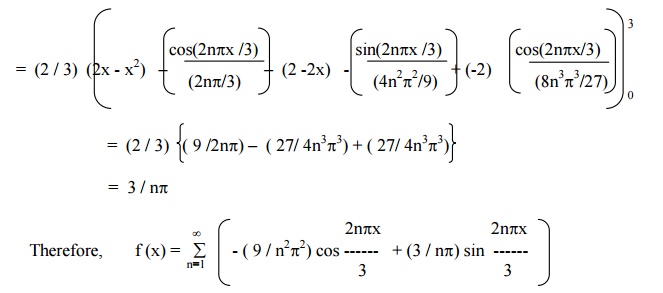
Exercises

1.Obtain the Fourier series for f(x) = px in 0 < x < 2. 2.Find the Fourier series to represent x2 in the interval (-l, l ). 3.Find a Fourier series in (-2, 2), if

f(x) = 0, -2 < x < 0

= 1, 0 < x < 2.                                  

4.Obtain the Fourier series for         

f(x) =          1-x in 0 < x < l               

= 0 in  l      < x < 2 l.     Hence deduce that

1- (1/3 ) +(1/5) –(1/7) p/4+&  â€¦   =

2                2        ) + (1/5        2                 2        

(1/1 ) + (1/3 )   +  p…/8) =   (

5.If f(x) = px,                          0 < x < 1              

= p (2-x), 1 < x < 2,                

Show that in the interval (0,2),

6.Obtain the Fourier series for                            

f(x) = x in 0 < x < 1                                             

= 0 in 1 < x < 2                                                   

7.Obtain the Fourier series for                            

f(x) =          (cx /l ) in 0 < x < l                             

=       (c/l  ) (2 l  - x ) in l          < x < 2 l .                       

8.Obtain the Fourier series for

f(x) = (l + x ), - l < x < 0. = (l - x ), 0 < x < l.

10.Express f(x) = x  as a half –range sine series in 0 < x < 2

11.Obtain the half-range  sine series for ex in 0 < x < 1.

12.Find the half –range cosine series for the function f(x) = (x-2)2 in the interval 0 < x < 2.