Chapter: Mathematics (maths) : Fourier Series
Even and Odd functions
Even and Odd functions
A function f(x) is said to be even if f (-x) = f (x). For example x2, cosx, x sinx, secx are even functions. A function f (x) is said to be odd if f (-x) = - f (x). For example, x3, sin x, x cos x,. are odd functions.
(1) The Euler‟s formula for even function is a
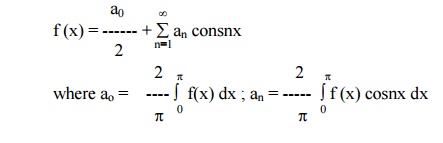
(2) The Euler‟s formula for odd function is
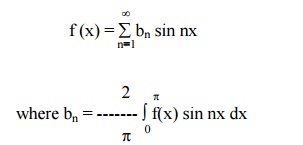
Example 6
Find the Fourier Series for f (x) = x in ( -p, p)
Here, f(x) = x is an odd function.
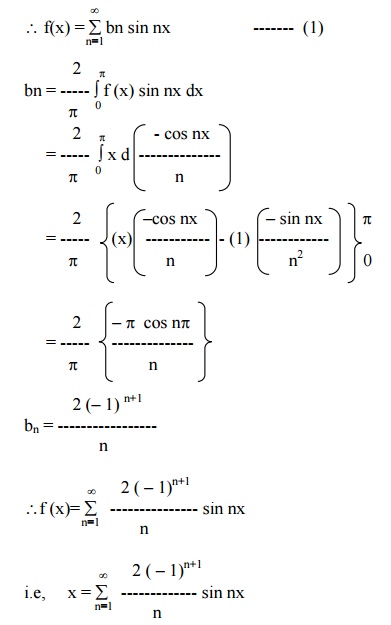
Example 7
Expand f (x) = |x| in (-p, p) as FS and hence deduce that


Example 8
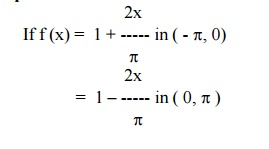
Then find the FS for f(x) and hence show that
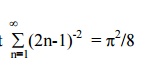
Here f (-x) in (-p,0) = f (x) in (0,p)
f (-x) in (0,p) = f (x) in (-p,0)
f(x) is a even function
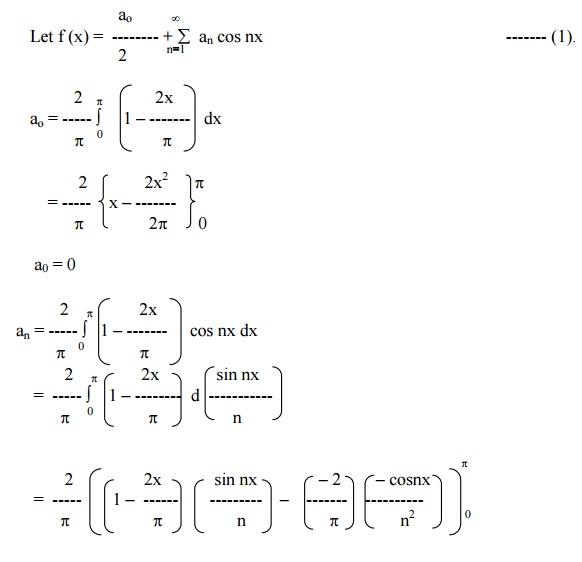
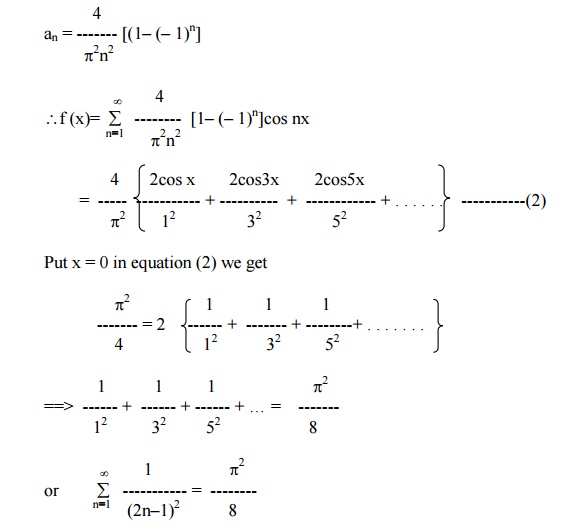
Example 9
Obtain the FS expansion of f(x) = x sinx in (-p< x<p) and hence deduce that

Here f (x) = xsinx is an even function.
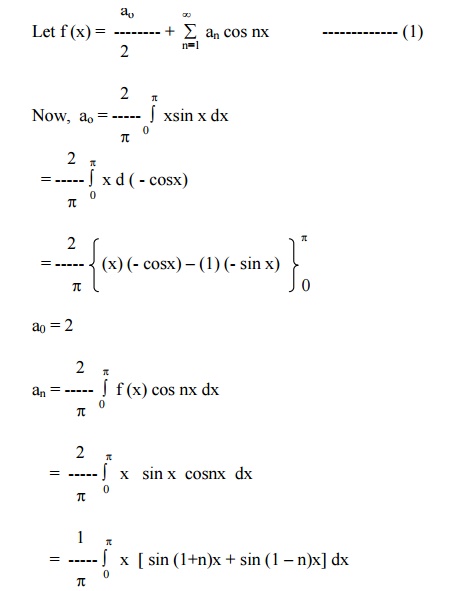

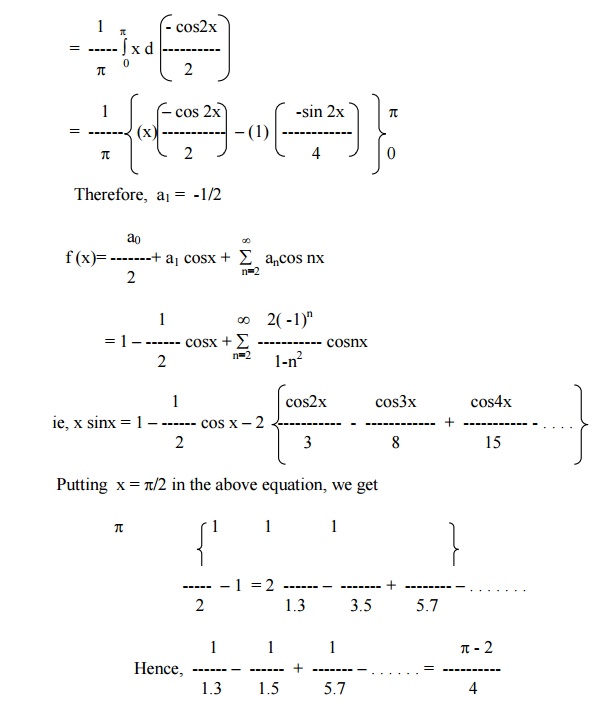
Exercises:
Determine Fourier expressions of the following functions in the given interval:
i. f(x) = p/2 + x, -p< x < 0
p/2 - x, 0 < x < p
ii. f(x) = -x+1 for + -p< x < 0
x+1 for 0 =< x =< p
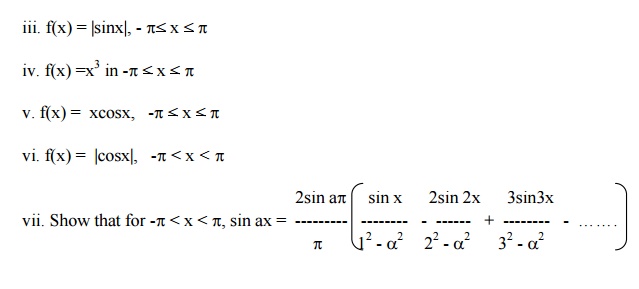
Related Topics