Lagrange’s Linear Equation

Lagrange’s   Linear   Equation

Equations of the form Pp + Qq  = R ________ (1), where P, Q and R are functions   of x,   y,   z,   are   known   as   Lagrang solve this equation, let us consider the equations u = a  and v = b, where a, b are arbitrary constants and u, v are functions of x, y, z.

Equations (5) represent a pair of simultaneous equations which are of the first order and of first degree.Therefore, the two solutions of (5) are u = a and v = b. Thus, f( u, v ) = 0 is the required solution of (1).

Note :

To solve the Lagrange‟s equation,we have to form the subsidiary or auxiliary  equations

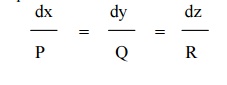
which can be solved either by the method of grouping or by the method of multipliers.

Example 21

Find the  general solution of px + qy = z.

Here, the subsidiary equations are

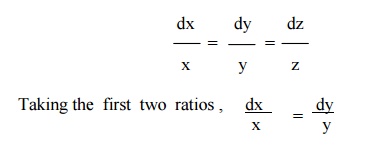
Integrating, log x = log y + log c1

or x = c1 y i.e, c1 = x / y

From the last two ratios,

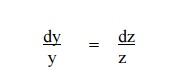
Integrating, log y = log z  + log c2

or  y = c2 z         

i.e,  c2 = y / z         

Hence the required  general solution is  

Φ(   x/y,=  0,y/z)where Φ is   arbitrary

Example 22 

Solve  p tan x + q tan y  = tan z 

The subsidiary equations are       

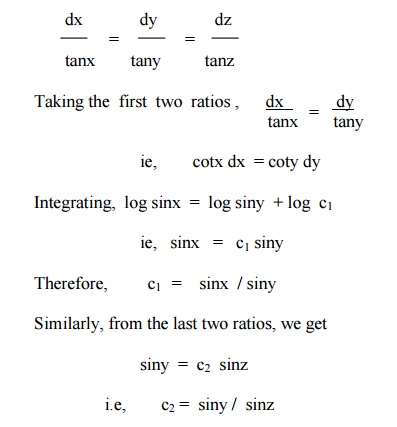
Hence the required  general solution is  

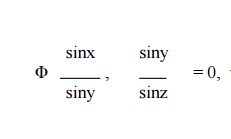
where Φ is   arbitrary

Example 23                   

Solve (y-z) p + (z-x) q  = x-y

Here the subsidiary equations are

Example 24

Find the general solution of  (mz  - ny) p  + (nx- lz)q = ly - mx.

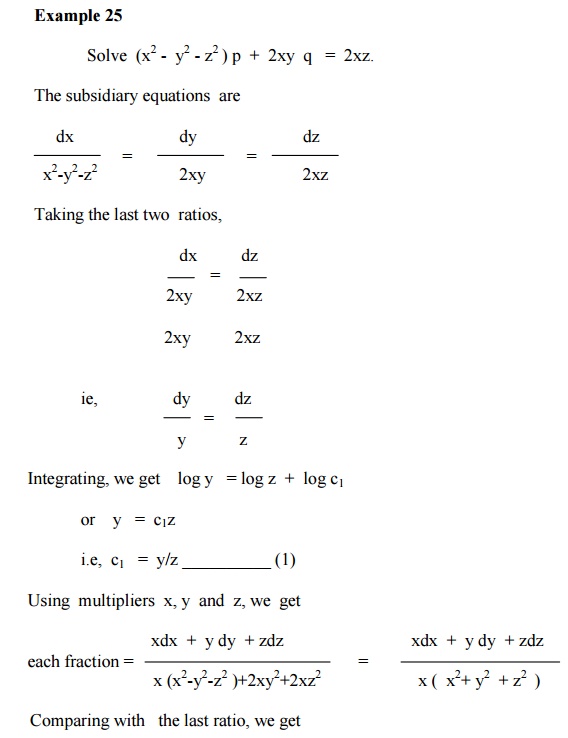
Exercises

Solve the following equations

1.     px2 + qy2 = z2

2.     pyz + qzx = xy 

3.     xp –yq = y2 â€“x2

4.     y2zp + x2zq = y2x 

5.     z (x –y) = px2 â€“qy2

6.     (a –x) p + (b –y) q = c –z 

7.  (y2z p) /x  + xzq = y2

8.     (y2 + z2) p –xyq + xz = 0 

9.     x2p + y2q = (x + y) z 

10.                      p –q = log (x+y) 

11.                      (xz + yz)p + (xz –yz)q = x2 + y2

12.                      (y –z)p –(2x + y)q = 2x + z