Chapter: Mathematics (maths) : Partial Differential Equations
Formation of Partial Differential Equations
Formation of Partial Differential Equations
Partial differential equations can be obtained by the elimination of arbitrary constants or by the elimination of arbitrary functions.
By the elimination of arbitrary constants
Let us consider the function
f( x, y, z, a, b ) = 0 ------------- (1)
where a & b are arbitrary constants
Differentiating equation (1) partially w.r.t x & y, we get
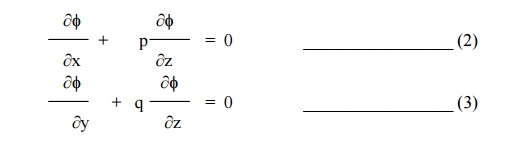
Eliminating a and b from equations (1), (2) and (3), we get a partial differential equation of the first order of the form f (x,y,z, p, q) = 0
Example 1
Eliminate the arbitrary constants a & b from z = ax + by + ab
Consider z = ax + by + ab ____________ (1)
Differentiating (1) partially w.r.t x & y, we get
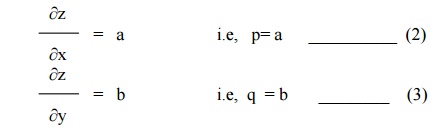
Using (2) & (3) in (1), we get
z = px +qy+ pq
which is the required partial differential equation.
Example 2
Form the partial differential equation by eliminating the arbitrary constants a and b from
z = ( x2 +a2 ) ( y2 + b 2)
Given z = ( x2 +a2 ) ( y2 + b2) ……..(1)
Differentiating (1) partially w.r.t x & y , we get
p = 2x (y2 + b2 )
q = 2y (x + a )
Substituting the values of p and q in (1), we get
4xyz = pq
which is the required partial differential equation.
Example 3
Find the partial differential equation of the family of spheres of radius one whose centre lie in the xy - plane.
The equation of the sphere is given by
( x –a )2 + ( y- b) 2 + z2 = 1 _____________ (1)
Differentiating (1) partially w.r.t x & y , we get
2 (x-a ) + 2 zp = 0
2 ( y-b ) + 2 zq = 0
From these equations we obtain
x-a = -zp _________ (2)
y -b = -zq _________ (3)
Using (2) and (3) in (1), we get
z2p2 + z2q2 + z 2 = 1
or z2 ( p2 + q2 + 1) = 1
Example 4
Eliminate the arbitrary constants a, b & c from

and form the partial differential equation.
The given equation is

or -zp + xzr + p2x = 0
By the elimination of arbitrary functions
Let u and v be any two functions arbitrary function. This relation can be expressed as
u = f(v) ______________ (1)
Differentiating (1) partially w.r.t x & y and eliminating the arbitrary functions from these relations, we get a partial differential equation of the first order of the form
f(x, y, z, p, q ) = 0.
Example 5
Obtain the partial differential equation by eliminating „f„from z = ( x+y ) f ( x2 - y2 )
Let us now consider the equation
z = (x+y ) f(x2- y2) _____________ (1)
Differentiating (1) partially w.r.t x & y , we get
p = ( x + y ) f ' ( x2 - y2 ) . 2x + f ( x2 - y2 )
q = ( x + y ) f ' ( x2 - y2 ) . (-2y) + f ( x2 - y2 )

i.e, py - yf( x2 - y2 ) = -qx +xf ( x2 - y2 )
i.e, py +qx = ( x+y ) f ( x2 - y2 )
Therefore, we have by(1), py +qx = z
Example 6
Form the partial differential equation by eliminating the arbitrary function f
from
z = ey f (x + y)
Consider z = ey f ( x +y ) ___________ ( 1)
Differentiating (1) partially w .r. t x & y, we get
p = ey f ' (x + y)
q = ey f '(x + y) + f(x + y). ey
Hence, we have
q = p + z
Example 7

Exercises:
1. 1. Form the partial differential equation by eliminating the arbitrary constants „a‟ & „b‟ from the following equations.
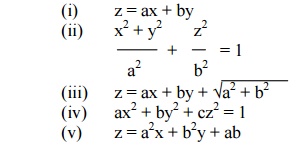
2. Find the PDE of the family of spheres of radius 1 having their centres lie on the xy plane{Hint: (x –a)2 + (y –b)2 + z2 = 1}
3. Find the PDE of all spheres whose centre lie on the (i) z axis (ii) x-axis
4. Form the partial differential equations by eliminating the arbitrary functions in the following cases.
(i) z = f (x + y)
(ii) z = f (x2 –y2)
(iii) z = f (x2 + y2 + z2)
(iv) f(xyz, x + y + z) = 0
(v) F (xy + z2, x + y + z) = 0
(vi) z = f (x + iy) +f (x –iy)
(vii) z = f(x3 + 2y) +g(x3 –2y)
Related Topics