Chapter: Mathematics (maths) : Partial Differential Equations
Important Questions and Answers: Partial Differential Equations
PARTIAL DIFFERENTIAL EQUATIONS
1. Explain
how PDE are formed?
PDE can be obtained
(i)
By eliminating the arbitrary constants
that occur in the functional relation between the dependent and independent
variables.
(ii) By
eliminating arbitrary functions from a given relation between the dependent and
independent variables.
2.From the PDE by
eliminating the arbitrary constants a & b from z
=ax +by
.
Given z =ax
+by
Diff. p.w.r. to x we
get,
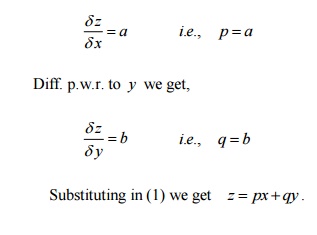
3. From the PDE by
eliminating the arbitrary constants a & b from

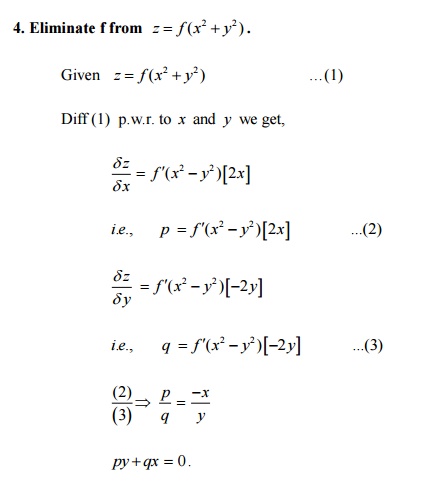
5.
Obtain PDE from z =f (sin x + cos y) .
Given z =f
(sin x +cos y) …(1)
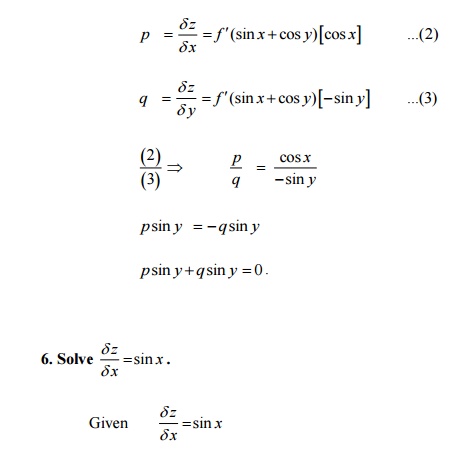
Integrating
w.r to x on both sides
z
= -cos x c+
But
z is a function of x and y
\ z =-cos x f+(y)
Hence c =f ( y) .
7. Mention three types of solution of a
p.d.e (or) Define general and complete integrals of a
p.d.e.
(i) A
solution which contains as many arbitrary constants as there are independent
variables is called a complete integral (or) complete solution.
(ii) A
solution obtained by giving particular values to the arbitrary constants in a
complete integral is called a particular integral (or) particular solution.
(iii)A solution of a p.d.e which
contains the maximum possible number of arbitrary functions is called a general
integral (or) general solution.
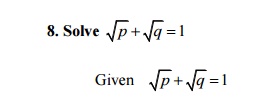
This
is of the form F(p,q) = 0.
Hence
the complete integral is z =ax +by cz.
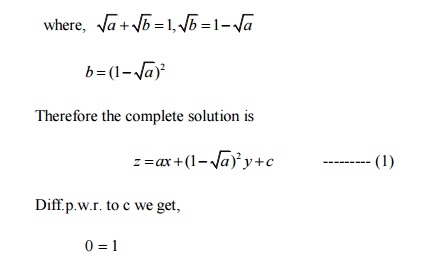
There
is no singular integral.
Taking c
=f
(a)when f is arbitrary.

Eliminating ' a ' between (2) & (3) we get the general
solution.
9. Find the complete integral of
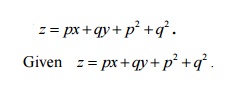
This equation is of the form z =px
+qy f+(p, q) .
By
Clairaut’s type,put
Therefore the complete integral is

10.
Find the complete integral of q =2 px
.
Given q
=2 px .
This equation of the form f (x, p, q) =0 .
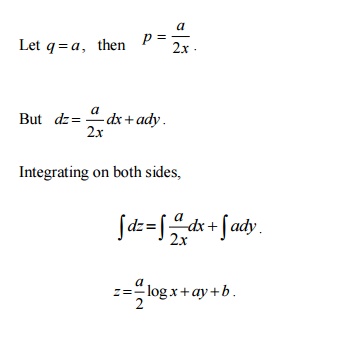
11. Find the complete integral of pq
=xy
.
Given pq
=xy .
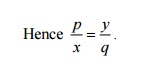
It is of the form
f (x, p ) =f(y
, q) .
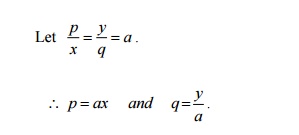
Hence dz =pdx +qdy
.



The given differential equation
can be written as,
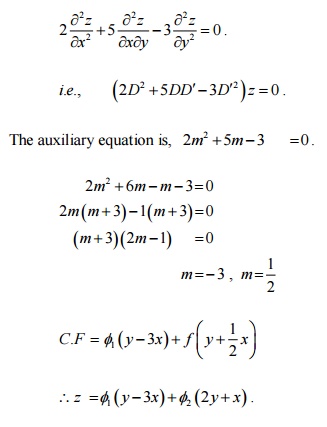


Where a & b are arbitrary constant.
To Find The Singular integral:
Diff (1)
p.w.r.to a,
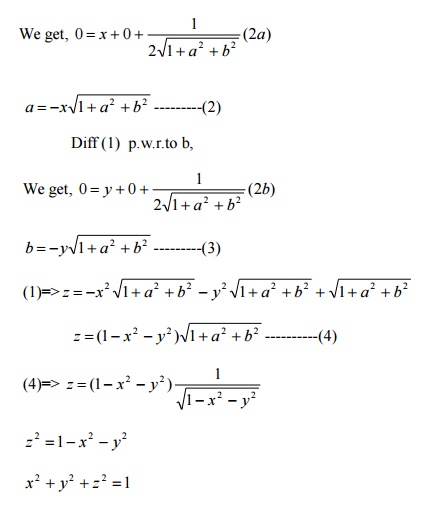
Which is the singular solution.
To Get the general integral:
Put b =f(a)
in (1) , we get
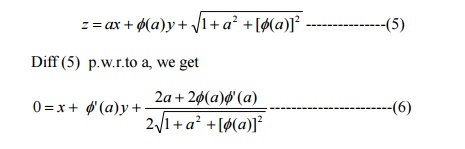
Eliminate a between (5) abd (6) to get the general
solution.
2.Solve y2p-xyq=x(z-2y)
Soln:
Given y2p-xyq=x(z-2y)
This equation of the form Pp+Qq=R
Here, P=y2 ,Q=-xy , R= x(z-2y)

Hence the general solution is f(x2+y2
, yz-y2)=0.
3.Solve:(3z-4y)p+(4x-2z)q=2y-3x
Soln:
Given: (3z-4y)p+(4x-2z)q=2y-3x
This equation of the form Pp+q=R
Here, P= (3z-4y)
,Q=(4x-2z) , R= 2y-3x
Again use Lagrangian multipliers 2,3,4,

2x+3y+4z=b.
Hence the general solution is,
F(x2+y2+z2 ,
2x+3y+4z)=0.
4.Find the general solution of x(y2-z2)p+y(z2-x2)q=z(x2-y2)
Soln;
Given; x(y2-z2)p+y(z2-x2)q=z(x2-y2)
This equation of the form Pp+q=R
Here, P= x(y2-z2) ,Q= y(z2-x2)
, R= z(x2-y2)
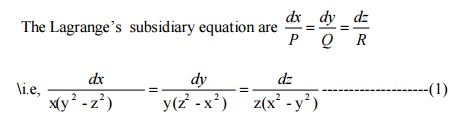
Use Lagrangian multipliers x,y,z,
We get the ratio in (1)

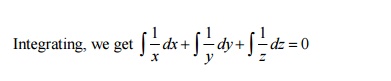
logx +logy+logz=log b
Hence the general solution is,
F(x2+y2+z2 , logx +logy+logz)=0.
The auxiliary equation is m3-2m2=0
Replace
D by m
and D’ by 1
m2(m-2)=0
m=0,0 and m=2
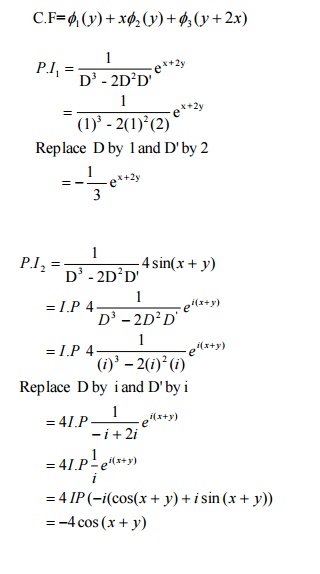
=4 IP (-i(cos(x +y) +i sin (x +y))
=-4 cos (x +y)
Hence the general solution is
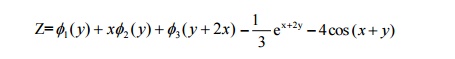
Related Topics