Chapter: Mathematics (maths) : Advanced Queueing Models
Important Short Objective Questions and Answers: Non-Markovian Queues and Queue Networks
Non- Markovian Queues and Queue Networks
1. Write down pollaczek-Khintchine
formula and explain the notations .
If T is the
random service time, the average number of customers in the system
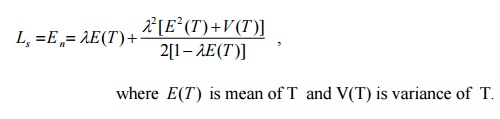
M/G/1
queueing system is markovian comment on this statement.
M/G/1 queueing system is a non markovian queue
model. Since the service time follows general distribution.
2. What
do you mean by regeneration points in ( M/G/1 ) model?
The point at which the nth units completes his
service and leaves the system.
3.Write down pollaczek-Khintchine
transform formula.
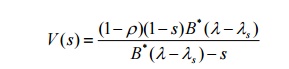
4. In ( M/G/1 ) model write the
formula for the average in the system.
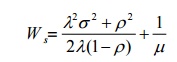
Queue
Networks
5. Write
classification of Queueing Networks.
¬ Open
Networks
¬ Closed
Networks
¬ Mixed
Network
7.State
arrival theorem .
In the closed networks system with m customers, the
system as seen by arrivals to server j is distributed as the stationary
distribution in the same network system when there are only m-1 customers.
8. Distinguish between open and
closed network.
Open Networks
1. Arrivals
from outside to the node i(ri ) is allowed.
2. Once the
customer gets the service completed at node i, he joins the queue at node j
with probability pij or leaves the system with probability pi0
Closed Networks
1. New customer never enter in to the
system.
2. Existing customer never depart from the system (ie) pi0 = 0 and ri = 0 or
all I (OR) No c ustomer may leave the system.
9. Explain (series queue) tandem queue model.
A series queue or a tandem queue model
is satisfies the following characteristics.
¬ Customers
may arrive from outside the system at any node and may leave the system from
any node.
¬ Customers
may enter the system at some node, traverse from node to node in the system and
leave the system from some node, necessarily following the same order of nodes.
¬ Customers
may return to the nodes aiready visited, skip some nodes and even choose to
remain in the system for ever.
10.Define
an open Jackson network.
Suppose a queueing network consists of k
nodes is called an open Jackson network, if it satisfies the following
characteristics.
¬ Customers arriving at node k from outside the system arrive in a Poission pattern with the average arrival rate ri and join the queue at I and wait for his turn for service.
¬ Service
times at the channels at node I are independent and each exponentially
distributed wite parameter µ
.
¬ Once
a customer gets the service completed at node i, he joins the queue at node j
with probability pij ( whatever be the number of customers
waiting at j for service),
when i = 1,2,…,k and j = 1,2,…,k pi0
represents the probability that a customer leaves the system from the i after
getting the service at i
¬ The
utilization of all the queue is less than one.
11.Define
a closed Jackson network.
A queueing network of k nodes is called
a closed Jackson network, if new customer never enter into and the existing
customer never depart from the system. Viz. if ri = 0 and pi0
for all i.In other words, it is equivalent to a finite source queueing system
of N customers who traverse continuously inside the network where the service i
is exponentially distributed with rate µi , I =1,2,…,k
The customer completes the service at S
j ,j= 1,2,…,k with probability pij where it
is assumed that
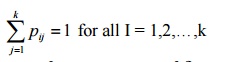
12.What
is meant by queue network?
A network of queues is a collection of
service centers, which represent system resources, and customers, which
represent users or transactions.
13.
What do you mean by M/G/1 queue.
In the M/G/1Queueing system under study
, we consider a single-server queueing system with infinite capacity, poission
arrivals and general service discipli8ne.The model has arbitrary service time,
and it is not necessary to be memoryless. Ie .it is not exponentiasl.
14. Write down the formula for the
steady-state probability P(n1,n2 ,...,nk
) for multiple server Jackson’s closed network.
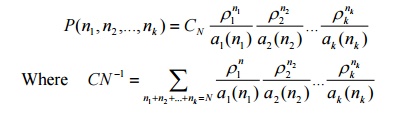
Related Topics