Chapter: Mathematics (maths) : Advanced Queueing Models
Advanced Queueing Models
ADVANCED QUEUEING MODELS
(M/G/I):(GD) queue
Pollaczek-Khintchine formula
M/D/1 and M/EK/1 as special cases
Series queues
Open Jackson Networks
1 Non-Markovian queues and Queue
Networking The M/G/1 queueing system (M/G/1) : (∞/GD)
mdel Pollaczek Ishintchine Formula
Let N and N1 be the
numbers of customers in the system at time t and t+T, when two consecutive customers
have just left the system after getting service.
Let k be the no. of customer arriving in
the system during the service time T.

Where k = 0, 1, 2, 3, … is the no. of
arrivals during the service time (K is a discrete random variable)
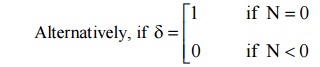
Then
N1 = N–1+δ+ k.
Various formula for (M/G/1) : (∞/GD)
Model can be summarized as follows:
1) Average no. of customer in the system

Example :5.1.1
Automatic car wash
facility operates with only one bay cars arrive according to a Poisson
distribution with a mean of 4 cars per hour and may wait in the facility's
parking let if the bay is busy. The parking lot is large enough to accommodate
any no. of cars. If the service time for all cars is constant and equal to
community determine.
(1) Mean
no. of customers in the system LS
(2) Mean
no. of customers in the queue Lq
(3) Mean
waiting time of a customer in the system WS
(4) Mean
waiting time of a customer in the system Wq
This
is (M/G/I) : (∞/GD) model. Hence λ=
4 cars / hour.
T
is the service time & is constant equal to 10 minutes
Then E(T) = 10 minutes
& V(T) = 0.

Example :5.1.2 A
car wash facility operates with only one day. Cars arrive according to a
Poisson distribution with a mean of 4 cars per hour and may wait in the
factory's parking lot in the bay is busy. The parking lot is large enough to
accommodate any no. of cars. If the service time for a car has uniform
distribution b/w 8 & 12 minutes, find (i) The avg. no. of cars waiting in
the parking lot and (ii) The avg. waiting time of car in the parking lot.
Solution

= 0.675
cars
The avg. no. of cars
waiting in the parking lot = 0.675 crs The avg. waiting time of a car in the
parking lot
= L q/λ =0.675 x 15
Wq = 10.125 minutes .
2 QUEUE NETWORKS
Queue in series without possibility of
queueing steady - state probability
P(0, 0) = Prob. (that both stages are empty
P(1, 0) = Prob. (that
the 1st stage is full and the second is empty) P(1,1) = Prob. (that both the
stages are full, first is working) P(b1, 1) = Prob. (that first is blocked and
the second is full)
P(0, 1) = Prob. (that 1st stage is empty and the
second is full)
2.1 STEADY STATE EQUATION
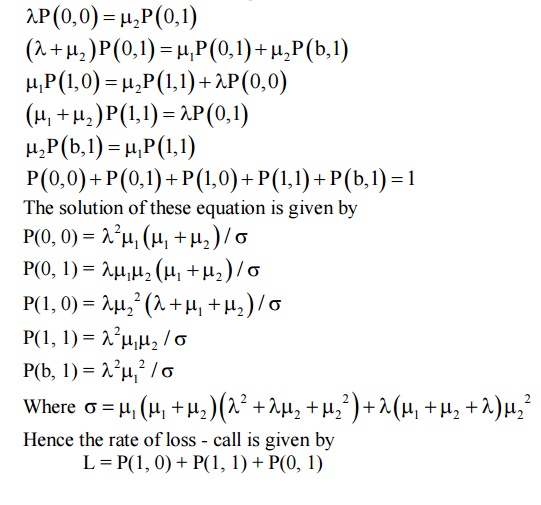
Example :5.2.1 A
repair facility shared by a large no. of machines has two sequential stations
with respective rates one per hour and two per hour. The cumulative failure
rate of all machines is 0.5 per hour. Assuming that the system behaviour may be
approximated by the two-stage tandem queue, determine (i) the avg repair time
(ii) the prob. that both service stations are idle (iii) the station which is
the bottleneck of the service facility.
Given

Example :5.2.2
Consider the
open central server queueing model with two I/O channels with a common service
rate of 1.2 sec–1. The CPU service rate is 2 sec–1, the
arrival rate is 1/7 jobs / second. The branching prob. are given by P0 = 0.7,
P1 = 0.3 and P2 = 0.6. Determine the steady state prob., assuming the service
times are independent exponentially distributed random variables.
Determine the queue length distributions
at each node as well as the avg. response time from the source on the sink.
We are given
µ1 = 1.2 / second
µ2 = 1.2 / second



TUTORIAL
PROBLEMS
1. Derive
the Balance equation of the birth and death process.
2. Derive
the Pollaczek-Khinchine formula.
3. Consider
a single server, poisson input queue with mean arrival rate of 10hour currently
the server works according to an exponential distribution with mean service
time of 5minutes. Management has a training course which will result in an
improvement in the variance of the service time but at a slight increase in the
mean. After completion of the course;, its estimated that the mean service time
will increase to 5.5 minutes but the standard deviation will decrease from 5 minutes
to 4 minutes. Management would like to know; whether they should have the server undergo
further training.
4. Ina heavy machine
shop, the over head crane is 75%utilized.Time study observations gave the
average slinging time as 10.5 minutes with a standard deviation
of 8.8 minutes.What is the average call ingrate for the services of the crane and
what is the average delay in getting service? If the average service time is
cut to 8.0 minutes, with standard deviation of 6.0 minutes, how much reduction will
occur, on average, in the delay of getting served?
4. Automatic
car wash facility operates with only on Bay. Cars arrive according toa Poisson
process, with mean of 4 carsperhour and may wait in the facility’s parking lot
if the bay is busy. If the service time for all cars is constant and equal to
10 min, determine Ls, Lq,Ws and Wq
WORKED OUT EXAMPLES
Example :1 A
car wash facility operates with only one day. Cars arrive according to a Poisson
distribution with a mean of 4 cars per hour and may wait in the factory's
parking lot in the bay is busy. The parking lot is large enough to accommodate
any no. of cars. If the service time for a car has uniform distribution b/w 8
& 12 minutes, find (i) The avg. no. of cars waiting in the parking lot and
(ii) The avg. waiting time of car in the parking lot.
Solution

= 0.675
cars
The avg. no. of cars waiting in the
parking lot = 0.675 crs The avg. waiting time of a car in the parking lot
= Lq/λ =0.675 x 15
Wq
= 10.125 minutes .
Related Topics