Chapter: Mathematics (maths) : Queueing Theory
Important Short Objective Questions and Answers: Queueing Theory
Queueing Theory
1) What is meant by queue Discipline ?
Answer:
It Specifies the manner in which the customers from the queue or equivalently the manner in which they are selected for service, when a queue has been formed. The most common discipline are
(i) FCFS (First Come First Served) or First In First Out (FIFO)
(ii) LCFS (Last Come First Served)
(iii) SIRO (Service in Random Order)
2) Define Little’s formula
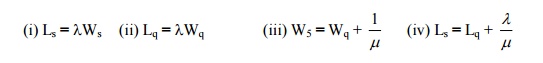
3) If people arrive to purchase cinema tickets at the average rate of 6 per minute, it takes an average of 7.5 seconds to purchase a ticket. If a person arrives 2 minutes before the picture starts and if it takes exactly 1.5 minutes to reach the correct seat after purchasing the ticket. Can he expect to be seated for the start of the picture ?
Answer:

4) If λ, µ are the rates of arrival and departure in a M/M/I queue respectively, give the formula for the probability that there are n customers in the queue at any time in steady state.
Answer:

5) If λ, µ are the rates of arrival and departure respectively in a M/M/I queue, write the formulas for the average waiting time of a customer in the queue and the average number of customers in the queue in the steady state.
Answer:
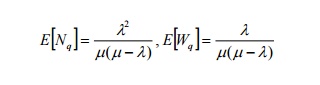
6) If the arrival and departure rates in a public telephone booth with a single phone are
1/12 and1 /14 respectively, find the probability that the phone is busy.
Answer:
P[Phone is busy] = 1 – P [ No customer in the booth]
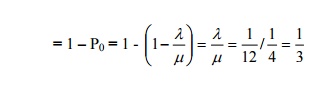
7) If the inter-arrival time and service time in a public telephone booth with a single-phone follow exponential distributions with means of 10 and 8 minutes respectively, Find the average number of callers in the booth at any time.
Answer:
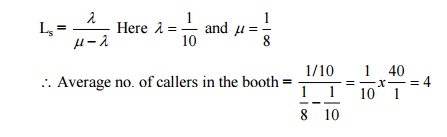
8) If the arrival and departure rates in a M/M/I queue are 1/2 per minute and 2/3 per minute respectively, find the average waiting time of a customer in the queue.
Answer:
Average waiting time of a customer in the queue
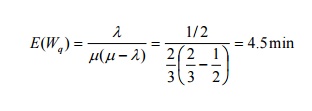
9) Customers arrive at a railway ticket counter at the rate of 30/hour. Assuming Poisson arrivals, exponential service time distribution and a single server queue (M/M/I) model, find the average waiting time (before being served) if the average service time is 100 seconds.
Answer:
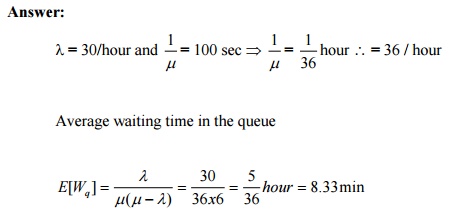
10) What is the probability that a customer has to wait more than 15 minutes to get his service completed in (M/M/I) : (∞ / FIFO) queue systme if λ = 6 per hour and µ = 10 per hour ?
Answer:
probability that the waiting time of a customer in the system exceeds time t=e−(µ −λ )t
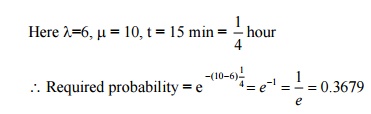
11) For (M/M/I) : (∞ / FIFO) model, write down the Little’s formula.
Answer:
(i) E(Ns) = λE(Ws)
(ii) (ii) E(Nq) = λE(Wq)
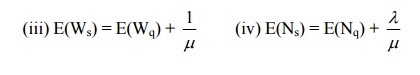
12) Using the Little’s formula, obtain the average waiting time in the system for M|M|1|N model.
Answer:
By the modified Little’s formula,
E(WS) = 1/ λ′ E (NS) where λ′ is the effective arrival rate.
13) For (M/M/I) : (∞ / FIFO) model, write down the formula for a. Average number of customers in the queue
b. Average waiting time in the system.
Answer:

14) What is the probability that a customer has to wait more than 15 minutes to get his service completed in M|M|1 queuing system, if λ = 6 per hour and µ = 10 per hour ? Answer:
Probability that the waiting time in the system exceeds t is

15) What is the probability that an arrival to an infinite capacity 3 server Poisson queuing

P [with out waiting] = P [N < 3 ] = P0 + P1 + P2
16) Consider an M|M|1 queuing system. If λ = 6 and µ = 8, Find the probability of atleast 10 customers in the system.
Answer:
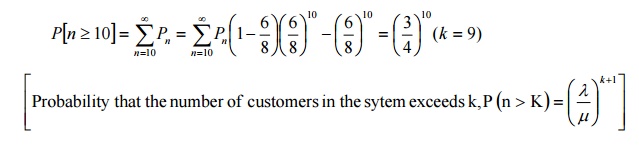
17) Consider an M|M|C queuing system. Find the probability that an arriving customer is forced to join the queue.
Answer:

18) Write down Pollaczek-Khinchine formulae.

19) Consider an M|M|1 queueing system. Find the probability of finding atleast ‘n’ customers in the system.
Answer:
Probability of at least n customers in the system

20) Consider an M|M|C queueing system. Find the probability that an arriving customer is forced to join the queue.
Answer:
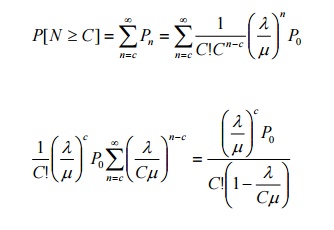
21.Briefly describe the M|G|1 queuing system. Answer:
Answer:
Poisson arrival / General service / Single server queuing system.
22) Arrivals at a telephone booth are considered to be Poisson with an average time of 12 minutes between one arrival and the next. The length of a phone call is assumed to be exponentially distributed with mean 4 min. What is the probability that it will take him more than 10 minutes altogether to wait for the phone and complete his call ?
Answer:
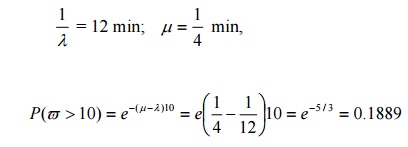
23) Customers arrive at a one-man barber shop according to a Poisson process with mean inter-arrival time of 12 minute, Customers spend an average of 10 min in the barber’s chair. What is the expected number of customers in the barber shop and in the quene ? How much time can a customer expect to spend in the barber’s shop ?
Answer:

24)A duplication machine maintained for office use is operated by office assistant. The time to complete each job varies according to an exponential distribution with mean 6 min. Assume a Poisson input with an average arrival rate of 5 jobs per hour. If an 8-hour day is used as a base, determine
a) The percentage of idle time of the machine.
b) The average time a job is in the system.
Answer:
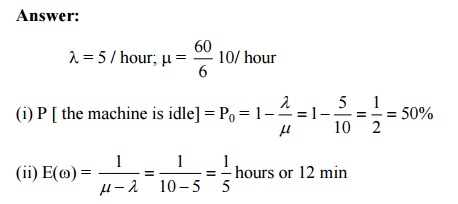
25 ) In a (M|M|1):(∞/F1F0) queuing model, the arrival and service rates are λ = 12/ hour
and µ = 24/hour, find the average number of customers in the system and in the queue.
Answer:

26) Customers arrive at a one-man barber shop according to a Poisson process with a mean inter arrival time of 12 minute. Customers spend an average of 10 minutes in the barber’s chair, what is the probability that more than 3 customers are in the system ?
Answer:
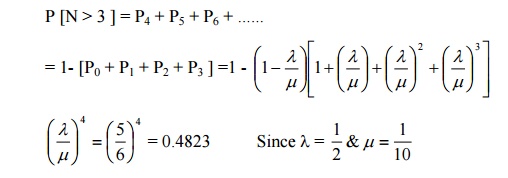
27) If a customer has to wait in a (M|M|1):(∞/F1F0) queue system what is his average waiting time in the queue, if λ = 8 per hour and µ=12 per hour ?
Answer:
Average waiting time of a customer in the queue, if he has to wait.
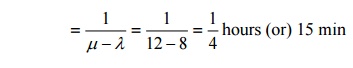
28) What is the probability that a customer has to wait more than 15 minutes to get his service completed in (M|M|1):(∞/F1F0) queue system, if λ = 6 per hour and µ = 10 per hour. Answer:
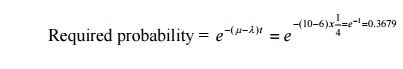
29) If there are two servers in an infinite capacity Poisson queue system with λ=10 and µ=15 per hour, what is the percentage of idle time for each server ?
Answer:
P [ the server will be idle] = P0
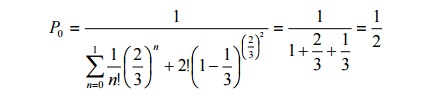
Percentage of idle time for each server = 50%
30) If λ = 4 per hour and µ = 12 per hour in an (M|M|1):(∞/F1F0) queuing system, find the probability that there is no customer in the system.
Answer:
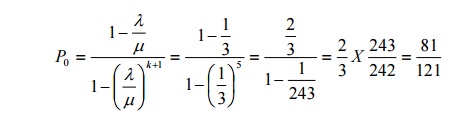
Related Topics