Output Equations and Main Dimensions of DC Machine

DC MACHINES

Introduction:

The size of the DC machine depends on the main or leading dimensions of the machine viz., diameter of the armature D and armature core length L. As the output increases, the main dimensions of the machine D and L also increases.

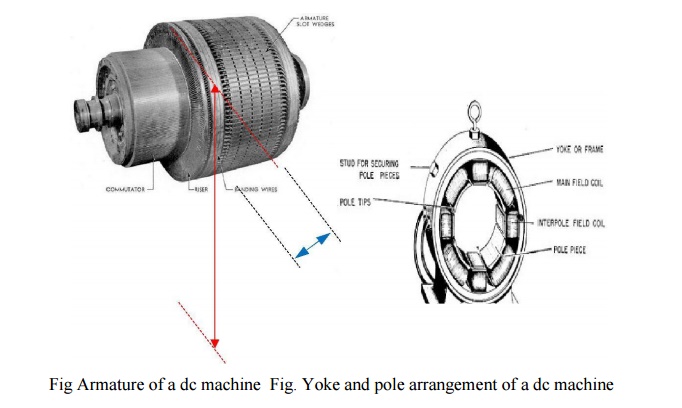
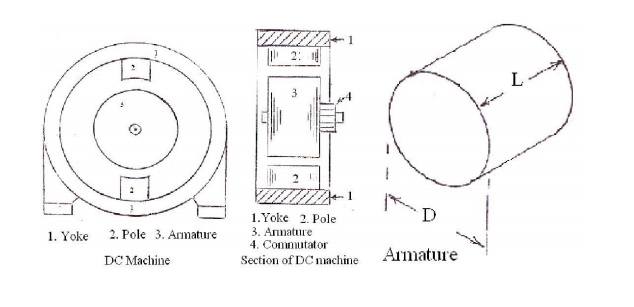
Output Equations and Main Dimensions of DC Machine

Note: Output equation relates the output and main dimensions of the machine. Actually it relates the power developed in the armature and main dimensions.

E : EMF induced or back EMF Ia : armature current

φ : Average value of flux / pole

Z : Total number of armature conductors N : Speed in rpm

P : Number of poles

A : number of armature paths or circuits D : Diameter of the armature

L : Length of the armature core

Power developed in the armature in kW = E Ia x 10-3

=                                                                                                                                                                         (φ Z N P/60 A)× Ia× 10-3

=                                                                                                                                                                         (Pφ ) × (I a Z/A) × N x 10-3/60 ....... (1)

The term P φ represents the total flux and is called the magnetic loading. Magnetic loading/unit area of the armature surface is called the specific magnetic loading or average value of the flux density in the air gap Bav. That is,

Bav = Pφ /Ï€ DL Wb/m2 or tesla denoted by T

Therefore Pφ = Bav  Ï€ DL ................ (2)

The term (Ia Z/A) represents the total ampere-conductors on the armature and is called the electric loading. Electric loading/unit length of armature periphery is called the specific electric loading q. That is,

Where C0 is called the output coefficeint of the DC machine and is equal to 1.64 x 10-4 Bq. 

Therefore D2 L = (Kw/1.64 × 10-4 B q N) m3

The above equation is called the output equation. The D2L product represents the size of the machine or volume of iron used. In order that the maximum output is obtained /kg of iron used, D2L product must be as less as possible. For this, the values of q and Bav must be high.

Effect of higher value of q

Note: Since armature current Ia and number of parallel paths A are constants and armature diameter D must be as less as possible or D must be a fixed minimum value, the number of armature conductors increases as q = Ia Z / A Ï€ D increases.

a.                                                 As q increases, number of conductors increases, resistance increases, I2R loss increases and therefore the temperature of the machine increases. Temperature is a limiting factor of any equipment or machine.

b.                                                  As q increases, number of conductors increases, conductors/slot increases, quantity of insulation in the slot increases, heat dissipation reduces, temperature increases, losses increases and efficiency of the machine reduces.

c.                                                  As q increases, number of conductors increases, armature ampere-turns per pole ATa / pole = (Ia Z / 2 A P) increases, flux produced by the armature increases, and therefore the effect of armature reaction increases. In order to overcome the effect of armature reaction, field MMF has to be increased. This calls for additional copper and increases the cost and size of the machine.

d.                                                 As q increases, number of conductors and turns increases, reactance voltage proportional to (turns)2 increases. This leads to sparking commutation.

Effect of higher value of Bav

a.                                                 As Bav increases, core loss increases, efficiency reduces.

b.                                                 As Bav increases, degree of saturation increases, mmf required for the magnetic circuit increases. This calls for additional copper and increases the cost of the machine.

It is clear that there is no advantage gained by selecting higher values of q and Bav. If the values selected are less, then D2L will be large or the size of the machine will unnecessarily be high. Hence optimum value of q and Bav must be selected.

In general q lies between 15000 and 50000 ampere-conductors/m.

Lesser values are used in low capacity, low speed and high voltage machines. In general Bav lies between 0.45 and 0.75 T.

SEPARATION OF D2L PRODUCT

Knowing the values of kW and N and assuming the values of q and Bav, a value for 

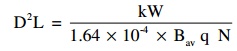
D2 L = kW/1.64 × 10-4× Bavq N can be calculated.

Let it be 0.1 m3.

Since the above expression has two unknowns namely D and L, another expression relating D and L must be known to find out the values of D and L.

Usually a value for the ratio armature core length L to pole pitch is assumed to separate D2L product. The pole pitch Ï„ refers to the circumferential distance corresponding one pole at diameter D. In practice L /Ï„ lies between 0.55 and 1.1.

Therefore L = (0.55 to 1.1) Ï„

= (0.55 to 1.1) π D / P

If L/τ = 1.0 and P = 4, then L = 1.0 × π D / P

= 1.0 × π D / 4 = 0.785D.

Therefore D2 × 0.785 D = 0.1 or D = 0.5m. Thus L = 0.785 × 0.5 = 0.395 m.

Note: The D2 L product can also be separated by assuming a value for the peripheral velocity of the armature.