Chapter: Mechanical : Heat and Mass Transfer : Phase Change Heat Transfer and Heat Exchangers
NTU Method
NTU METHOD:
Heat Exchangers Effectiveness - Useful
Parameters
In the design of heat
exchangers, the efficiency of the heat transfer process is very important. The
method suggested by Nusselt and developed by Kays and London is now being
extensively used. The effectiveness of a heat exchanger is defined as the ratio
of the actual heat transferred to the maximum possible heat transfer.
Let mh and mc
be the mass flow rates of the hot and cold fluids, ch and cc be the respective
specific heat capacities and the terminal temperatures be Th and T h for the
hot fluid at inlet and outlet, Thi and Th0 for the cold
fluid at inlet and outlet. By making an energy balance and assuming that there
is no loss of energy to the surroundings, we write
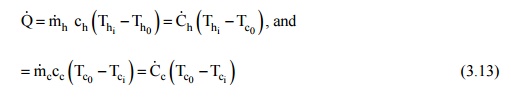
From Eq. (10.13), it
can be seen that the fluid with smaller thermal capacity, C, has the greater
temperature change. Further, the maximum temperature change of any fluid would
be
(Th
i -Tci )and this Ideal temperature change can be obtained
with the fluid which has the minimum heat capacity rate. Thus,

Or, the effectiveness
compares the actual heat transfer rate to the maximum heat transfer rate whose
only limit is the second law of thermodynamics. An useful parameter which also
measures the efficiency of the heat exchanger is the 'Number of Transfer
Units', NTU, defined as
NTU
= Temperature change of one fluid/LMTD.
Thus,
for the hot fluid: NTU = (Th i -Th0
)/LMTD , and
|
for the cold fluid: NTU T |
-T |
/ LMTD |
|
|
|
|

The heat exchanger would be more effective when the NTU is greater, and therefore,
NTU = AU/Cmin
(3.15)
An another useful
parameter in the design of heat exchangers is the ratio the minimum to the
maximum thermal capacity, i.e., R = Cmin/Cmax,
where R may vary
between I (when both fluids have the same thermal capacity) and 0 (one of the
fluids has infinite thermal capacity, e.g., a condensing vapour or a boiling
liquid).
Effectiveness - NTU Relations
For any heat exchanger,
we can write: Î=f (NTU, Cmin / Cmax ).In order to determine a specific form of the
effectiveness-NTU relation, let us consider a parallel flow heat exchanger for
which C min =Ch .
From the definition of effectiveness (equation 10.14), we get
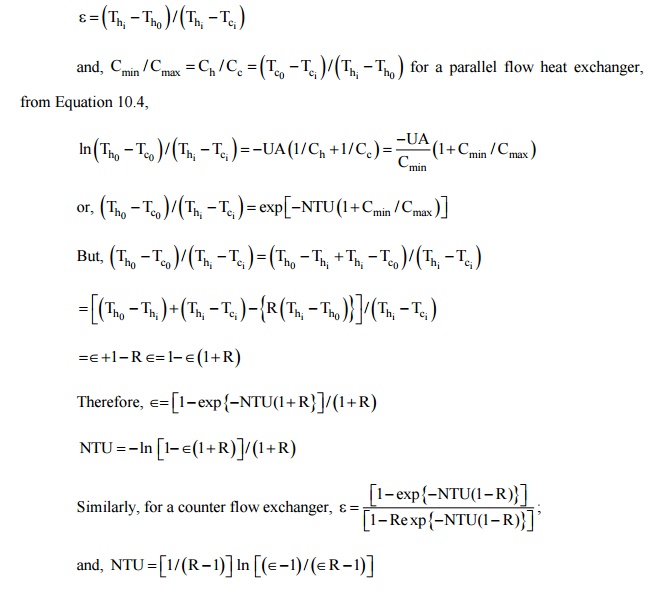
Heat Exchanger
Effectiveness Relation

Kays and London have
presented graphs of effectiveness against NTU for Various values of R
applicable to different heat exchanger arrangements,.

Related Topics