LMTD Method

LMTD METHOD :

Expression for Log Mean Temperature Difference - Its Characteristics

Fig.  represents a typical temperature distribution which is obtained in heat exchangers. The rate of heat transfer through any short section of heat exchanger tube of surface area dA is: dQ = U dA(T_h –T_c  cools and the cold fluid is heated in the direction of increasing area. therefore, we may write

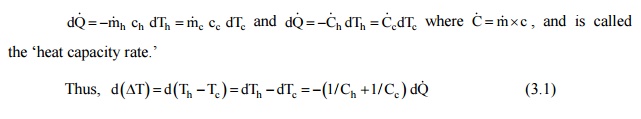
For a counter flow heat exchanger, the temperature of both hot and cold fluid decreases in the direction of increasing area, hence

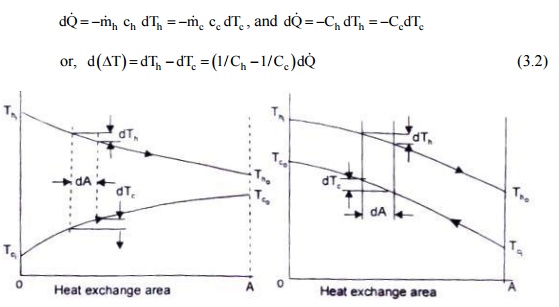
Fig. 3.9 Parallel flow and Counter flow heat exchangers and the temperature distribution with length

Integrating equations (3.1) and (3.2) between the inlet and outlet. and assuming that the specific heats are constant, we get

The positive sign refers to parallel flow exchanger, and the negative sign to the counter

(The assumption that U is constant along the heat exchanger is never strictly true but it may be a good approximation if at least one of the fluids is a gas. For a gas, the physical properties do not vary appreciably over moderate range of temperature and the resistance of the gas film is considerably higher than that of the metal wall or the liquid film, and the value of the gas film resistance effectively determines the value of the overall heat transfer coefficient U.)

It is evident from Fig.1 0.9 that for parallel flow exchangers, the final temperature of fluids lies between the initial values of each fluid whereas m counter flow exchanger, the temperature of the colder fluid at exit is higher than the temperature of the hot fluid at exit. Therefore, a counter flow exchanger provides a greater temperature range, and the LMTD for a counter flow exchanger will be higher than for a given rate of mass flow of the two fluids and for given temperature changes, a counter flow exchanger will require less surface area.

Special Operating Conditions for Heat Exchangers

(i)    Fig. 3.7a shows temperature distributions for a heat exchanger (condenser) where the hot fluid has a much larger heat capacity rate, C h = m _h c_h than that of cold fluid, Cc =m _c c_c and  therefore, the temperature of the hot fluid remains almost constant throughout the exchanger and the temperature of the cold fluid increases. The LMTD, in this case is not affected by whether the exchanger is a parallel flow or counter flow.

(ii) (ii) Fig. 3.7b shows the temperature distribution for an evaporator. Here the cold fluid expenses a change in phase and remains at a nearly uniform temperature Cc - > inf. The same effect would be achieved without phase change if  Cc >> Ch  and the LMTD will remain the same for both parallel flow and counter flow exchangers.

(iii)                       (iii) In a counter flow exchanger, when the heat capacity rate of uoth the fluids are equal, Cc  = Ch , the temperature difference is the same all along the length of the tube. And in that case, LMTD should be replaced by DT_a DT_b, and the temperature profiles of the two fluids  along Its length would be parallel straight lines.   

along Its length would be parallel straight lines.)

LMTD for Cross-flow Heat Exchangers :

LMTD given by Eq (10.6) is strictly applicable to either parallel flow or counter flow exchangers. When we have multipass parallel flow or counter flow or cross flow exchangers, LMTD is first calculated for single pass counter flow exchanger and the mean temperature difference is obtained by multiplying the LMTD with a correction factor F which takes care of the actual flow arrangement of the exchanger. Or,

The correction factor F for different flow arrangements are obtained from charts given.