Multistage impulse generator circuits

Multistage impulse generator circuits

The difficulties encountered with spark gaps for the switching of very high voltages, the increase of the physical size of the circuit elements, the efforts Generation of high voltages necessary in obtaining high dace. voltages to charge C1 and, last but not least, the difficulties of suppressing corona discharges from the structure and leads during the charging period make the one-stage circuit inconvenient for higher voltages. In order to overcome these difficulties, in 1923 Marx35 suggested an arrangement where a number of condensers are charged in parallel through high ohmic resistances and then discharged in series through spark gaps. There are many different, although always similar, multistage circuits in use. To demonstrate the principle of operation, a typical circuit is presented in Fig. 3.23 which shows the connections of a six-stage generator. The dace. Voltage charges the equal stage capacitors C01 in parallel through the high value charging resistors R0 as well as through the discharge (and also charging).

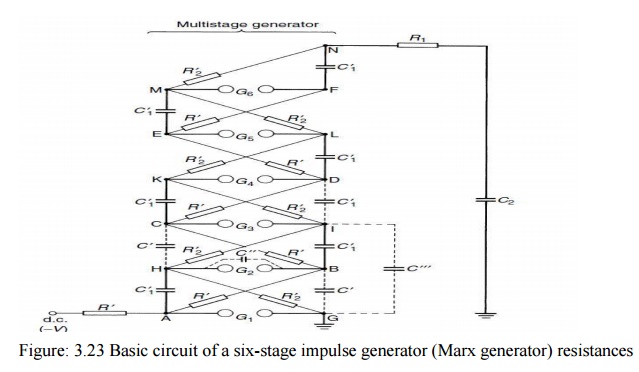
R02 which are much smaller than the resistors R0 and are comparable with R2 in Fig. 3.25. At the end of the relatively long charging period(typically several seconds up to 1 minute), the points A, B, . . . ,F will be at the potential of the dace. source, e.g. _V with respect to earth, and the pointsG,H,, N will remain at the earth potential, as the voltage drop during charging across the resistors R02is negligible. The discharge or firing of the generator is initiated by the breakdown of the lowest gap G1 which is followed by a nearly simultaneous breakdown of all the remaining gaps. According to the traditional theory, which does not take into account the stray capacitances Indicated by the dotted lines, this rapid breakdown would be caused by high over voltages across the second and further gaps: when the first gap fires, the potential at point A changes rapidly from _V to zero, and thus the point H increases its potential to CV.

As the point B still would remain at the charging potential, _V, thus a voltage of 2V would appear across G2. This high overvoltage would therefore cause this gap to break down and the potential at point I would rise to C2V, creating a potential difference of 3V across gapG3, if again the potential at point C would remain at the charging potential.

This traditional interpretation, however, is wrong, since the potentials B and C can – neglecting stray capacitances – also follow the adjacent potentials of the points A and B, as the resistors R0 are between. We may only see up to now that this circuit will give an output voltage with a polarity opposite to that of the charging voltage. In practice, it has been noted that the gap G2 must be set to a gap distance only slightly greater than that at which G1 breaks down; otherwise it does not operate.

According to Edwards, Husbands and Perry_31_ for an adequate explanation one may assume the stray capacitances C0, C00 and C000 within the circuit. The capacitances C0 are formed by the electrical field between adjacent stages; C000 has a similar meaning across two stages. C00 is the capacitance of the spark gaps. If we assume now the resistors as open circuits, we may easily see that the potential at point B is more or less fixed by the relative magnitudes of the stray capacitances. Neglecting C0 between the points Hand C and taking into account that the discharge capacitors C01 are large in comparison to the stray capacitances, point B can be assumed as mid-point of a capacitor voltage divider formed by C00 and C0/C000. Thus the voltage rise of point A from _V to zero will cause the potential B to rise from V to a voltage of

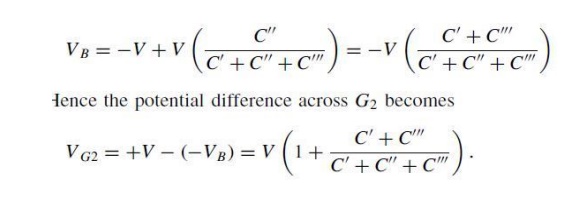
If C00 equals zero, the voltage across G2 will reach its maximum value 2V.This gap capacitance, however, cannot be avoided. If the stage capacitancesC0 and C000 are both zero, VG2 will equal V, and a sparking of G2 would not be possible. It is apparent, therefore, that these stray capacitances enhance favorable conditions for the operation of the generator. In reality, the conditions set by the above equations are approximate only and are, of course, transient, as the stray capacitances start to discharge via the resistors. As the values of C0 to C000 are normally in the order of some 10 pF only, the time constants for this discharge may be as low as 10_7 to 10_8 sec. Thus the voltage across G2 appears for a short time and leads to breakdown within several tens of nanoseconds. Transient over voltages appear across the further gaps, enhanced also by the fact that the output terminal N remains at zero potential mainly, and therefore additional voltages are built up across the resistor R02. So the breakdown continues and finally the terminal N attains a voltage of C6V, or nV, if n stages are present.

The processes associated with the firing of such generators are even more sophisticated. They have been thoroughly analyzed and investigated experimentally.31,36,37_In practice for a consistent operation it is necessary to set the distance for the first gap G1 only slightly below the second and further gaps for earliest breakdown. It is also necessary to have the axes of the gaps in one vertical plane so that the ultraviolet illumination from the spark in the first gap irradiates the other gaps. This ensures a supply of electrons released from the gap to initiate breakdown during the short period when the gaps are subjected to the overvoltage.

If the first gap is not electronically triggered, the consistency of its firing and stability of breakdown and therefore output voltage is improved by providing ultraviolet illumination for the first gap. These remarks indicate only a small part of the problems involved with the construction of spark gaps and the layout of the generator. Before some of these additional problems are treated, we shall treat more realistic Marx circuits as used for the explanations so far.

In Fig. 3.24, the wave front control resistor R1 is placed between the generator and the load only. Such a single ‘external’ front resistor, however, has to withstand for a short time the full rated voltage and therefore is inconveniently long or may occupy much space. This disadvantage can be avoided if either a part of this resistance is distributed or if it is completely distributed within the generator. Such an arrangement is illustrated in Fig. 2.30, in which in addition the series connection of the capacitors C01 and gaps (as proposed originally byGoodlet_38_) is changed to an equivalent arrangement for which the polarity of the output voltage is the same as the charging voltage. The charging resistorsR0 are always large compared with the distributed resistors R01and R02, andR02is made as small as is necessary to give the required time to halve-valueT2. Adding the external front resistor R001 helps to damp oscillations otherwise

R02: discharge resistors. R01: internal front resistors. R001: external front resistorexcited by the inductance and capacitance of the external leads between the generator and the load, if these leads are long. If the generator has fired, the total is charge capacitance C1 maybe calculated as where n is the number of stages. The consistent firing of such circuits could be explained as for the generator

of Fig. 3.24. For both generator circuits, the firing is aggravated if the resistancesR02 have relatively low values. According to equations such low values appear with generators of high energy content and/or short times to half-value, T2. Then the time constant for discharging the stray capacitances to ground C000 (Fig. 3.24) will be too low and accordingly the overvoltage for triggering the upper stages too short. By additional means providing high resistance values within the firing period, this disadvantage can be avoided.