Chapter: High Voltage Engineering : Generation of High Voltages and High Currents
Cockroft Walton Voltage Multiplier Circuit - Generation of High Voltages and Currents
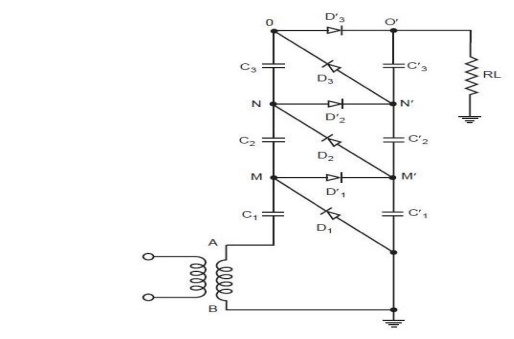
Cockroft-Walton Voltage Multiplier Circuit
In 1932, Cockroft and Walton suggested an improvement over the circuit developed by reinacher for producing high D.C. voltages. Fig. 3.3. Shows a multistage single phase cascade circuit of the Cockroft-Walton type. No Load Operation: The portion ABM′MA is exactly identical to Greinarcher voltage doublers circuit and the voltage across C becomes 2Vmax when M attains a voltage 2Vmax.During the next half cycle when B becomes positive with respect to
A, potential of M falls and, therefore, potential of N also falls becoming less than potential at M′ hence C2 is charged through D2. Next half cycle A becomes more positive and potential of M and N rise thus charging C′2 throughD′2. Finally all the capacitors C′1, C′2, C′3, C1, C2, and C3 are charged. The voltage across the column of capacitors consisting of C1, C2, C3, keeps on oscillating as the supply voltage alternates.
This column, therefore, is known as oscillating column. However, the voltage across the capacitances C′1, C′2, C′3, remains constant and is known as smoothening column. The voltages at M′, N′, and O′ are 2 Vmax 4 Vmax and 6 Vmax. Therefore, voltage across all the capacitors is 2 Vmax except for C1where it is Vmax only. The total output voltage is 2nVmax where n is the number of stages. Thus, the use of multistage arranged in the manner shown enables very high voltage to be obtained. The equal stress of the elements (both capacitors and diodes) used is very helpful and promotes a modular design of such generators.
Generator Loaded: When the generator is loaded, the output voltage will never reach the value 2n Vmax. Also, the output wave will consist of ripples on the voltage. Thus, we have to deal with two quantities, the voltage drop ΔV and the ripple δV.In 1932, Cockroft and Walton suggested an improvement over the circuit developed by Greinacher for producing high D.C. voltages. Fig. 2.3. shows a multistage single phase cascade circuit of the Cockroft-Walton type.
No Load Operation:
The portion ABM′MA is exactly identical to Greinarcher voltage doublers circuit and the voltage across C becomes 2Vmaxwhen Mattains a voltage 2Vmax.During the next half cycle when B becomes positive with respect to A, potential of M falls and, therefore, potential of N also falls becoming less than potential at M′ hence C2 is charged throughD2. Next half cycle A becomes more positive and potential of M and N rise thus charging C′2 throughD′2. Finally all the capacitors C′1, C′2, C′3, C, C2, and C3 are charged. The voltage across the column of capacitors consisting of C1, C2, C3, keeps on oscillating as the supply voltage alternates. This column, therefore, is known as oscillating column.
However, the voltage across the capacitances C′1,C′2, C′3, remains constant and is known as smoothening column. The voltages atM′, N′, and O are 2 Vmax 4 Vmax and 6 Vmax. Therefore, voltage across all the capacitors is 2 Vmax except for C1where it is Vmax only. The total output voltage is 2nVmax where n is the number of stages. Thus, the use of multistage arranged in the manner shown enables very high voltage to be obtained. The equal stress of the elements (both capacitors and diodes) used is very helpful and promotes a modular design of such generators.
Generator Loaded:
When the generator is loaded, the output voltage will never reach the value 2n Vmax. Also, the output wave will consist of ripples on the voltage. Thus, we have to deal with two quantities, the voltage drop V and the ripple Suppose a charge q is transferred to the load per cycle. This charge is q = I/f = IT. The charge comes from the smoothening column, the series connection of C′1, C′2, C′3,. If no charge were transferred during T from this stack via D1, D2, D3, to the oscillating column, the peak to peak ripple would merely be But in practice charges are transferred.
The process is explained with the help of circuits in Fig. 3.4 (a) and (b).Fig. 3.4 (a) shows arrangement when point A is more positive with reference to B and charging of smoothing column takes place and Fig. 3.4 (b) shows the arrangement when in the next half cycle Becomes positive with reference to A and charging of oscillating column takes place. Refer to Fig. 3.4(a). Say the potential of point O′ is now 6 Vmax. This discharges through the load resistance and say the charge lost is q = IT over the cycle. This must be regained during the charging cycle (Fig. 3.4 (a)) for stable operation of the generator.
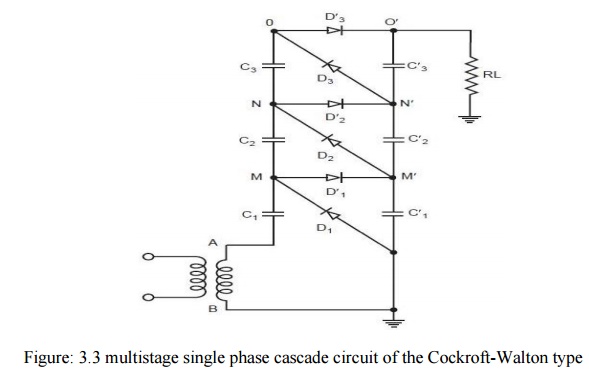

C3 is, therefore supplied a charge q from C3. For this C2 must acquire charge of 2q so that it can supply q charge to the load and q to C3, in the next half cycle termed by cockloft and Walton as the transfer cycle (Fig. 3.4 (b)). Similarly C′1 must acquire for stability reasons charge 3q so that it can supply a charge q to the load and 2q to the capacitor C2 in the next half cycle (transfer half cycle). During the transfer cycle shown in Fig. 3.4 (b), the diodes D1, D2, D3, conduct when B is positive with reference to A. Here C′2transfers q charge to C3, C1 transfers charge 2q to C2 and the transformer provides change 3q.For n-stage circuit, the total ripple will be
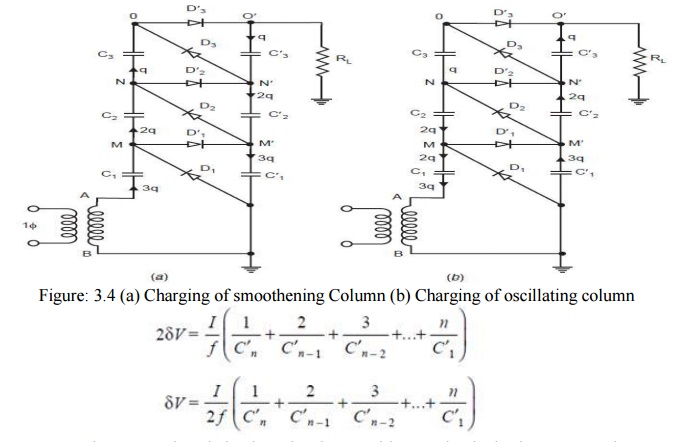
From above equation, it is clear that in a multistage circuit the lowest capacitors are responsible for most ripples and it is, therefore, desirable to increase the capacitance in the lower stages. However, this is objectionable from the view point of High Voltage Circuit where if the load is large and the load voltage goes down, the smaller capacitors (within the column) would be overstressed. Therefore, capacitors of equal value are used in practical circuits i.e., C′n = C′n – 1 =C′1 = C and the ripple is given as

The second quantity to be evaluated is the voltage drop ΔV which is the difference between the theoretical no load voltage 2nVmax and the on load voltage. In order to obtain the voltage drop ΔV refer to Fig. 3.4 (a).Here C′1 is not charged up to full voltage 2Vmaxbut only to 2Vmax – 3q/C because of the charge given up through C1 in one cycle which gives a voltage drop of 3q/C = 3I/fC The voltage drop in the transformer is assumed to be negligible. Thus, C2 is charged to the voltage.


To sum up we add the last term of all the terms (Tn through T1) and again add the last term of the remaining term and so on, i.e.,
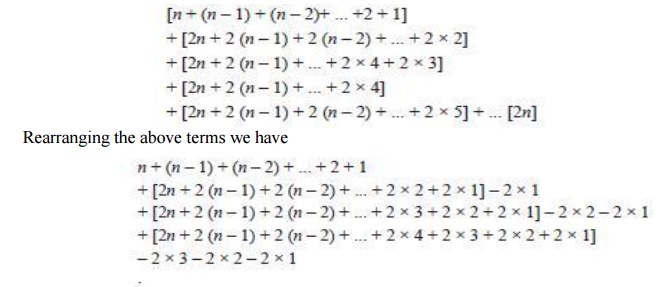

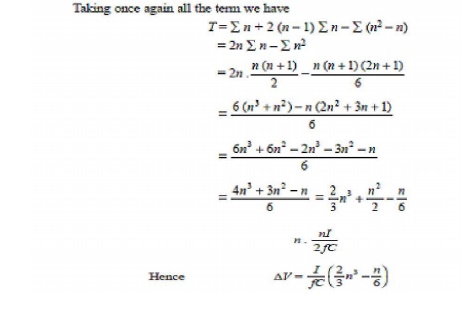
If n ≥4 we find that the linear term can be neglected and therefore, the voltage term approximated to
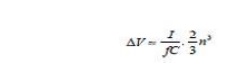
From above it is clear that for a given number of stages, a given frequency and capacitance of each stage, the output voltage decrease linearly with load current I. For a given load, however, V0= (V0max– V) may rise initially with the number of stages n, and reaches a maximum value but decays beyond on optimum number of stage. The optimum number of stages assuming a constant Vmax, I, f and C can be obtained for maximum value of V0 max by differentiating above equation with respect to n and equating it to zero

It is to be noted that in general it is more economical to use high frequency and smaller value of capacitance to reduce the ripples or the voltage drop rather than low frequency and high capacitance. Cascaded generators of Cockroft-Walton type are used and manufactured worldwide these days. A typical circuit is shown in Fig. 3.5. In general a direct current up to 20 mA is required for high voltages between 1 MV and 2 MV. In case where a higher value of current is required, symmetrical cascaded rectifiers have been developed. These consist of mainly two rectifiers in cascade with a common smoothing column. The symmetrical cascaded rectifier has a smaller voltage drop and also a smaller voltage ripple than the simple cascade. The alternating current input to the individual circuits must be provided at the appropriate high potential; this can be done by means of isolating transformer. Fig. 3.6 shows a typical cascaded rectifier circuit. Each stage consists of one transformer which feeds two half wave rectifiers.
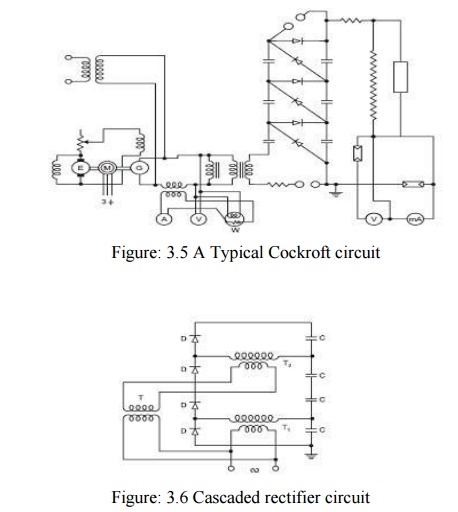
As the storage capacitors of these half wave rectifiers are series connected even the h.v. winding of T1 cannot be grounded. This means that the main insulation between the primary and the secondary winding of T1 has to be insulated for a dace. voltage of magnitude Vmax, the peak voltage of T1. The same is required for T2 also but this time the high voltage winding is at a voltage of 3Vmax. It would be difficult to provide the whole main insulation within this transformer, an isolating transformer T suppliesT2. The cascading of every stage would thus require an additional isolating transformer which makes this circuit less economical for more than two stages.
Related Topics