Theorems, Proof, Solved Example Problems - Multiplication Theorem on Probability | 11th Statistics : Chapter 8 : Elementary Probability Theory
Chapter: 11th Statistics : Chapter 8 : Elementary Probability Theory
Multiplication Theorem on Probability
Multiplication
Theorem on Probability
Theorem
8.5: (Multiplication Theorem of Probability)
If A and B are any two events of an experiment,
then
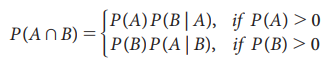
Proof:

Example 8.18
A box contains 7 red and 3 white marbles. Three marbles are
drawn from the box one after the other without replacement. Find the
probability of drawing three marbles in the alternate colours with the first
marble being red.
Solution:
The event of interest is drawing the marbles in alternate
colours with the first is red. This event can occur only when the marbles are
drawn in the order (Red , White , Red)
If A and C represent the events of drawing red
marbles respectively in the first and the third draws and B is the event of drawing white marble in the second draw, then the
required event is AŌł®B Ōł®C. The probability for the occurrence of A Ōł®B Ōł®C can be calculated applying
P(AŌł®BŌł®C) = P (A) P (B/A) P (C/AŌł® B)
Since there are 7 red and 3 white marbles in the box for the
first draw,
P(A) = 7/10
Now, there will be 6 red and 3 white marbles in the box for the
second draw if the event A has occurred. Hence,
P(B/A) = 3/9
Similarly, there will be 6 red and 2 white marbles in the box
for the third draw if the events A and B have occurred. Hence,
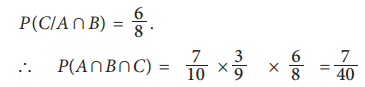
is the required
probability of drawing three marbles in the
alternate colours with the first marble being red.
Example 8.19
Three cards are drawn successively from a well-shuffled pack of
52 playing cards. Find the probability all three cards drawn successively is
ace without replacing the card after each draw.
Solution:
Let A: all the three cards drawn are aces
At the first draw, there will be 4 aces among 52 cards. Having
drawn an ace in the first draw, there will be 3 aces among 51 cards. Similarly,
there will be 2 aces among 51 cards for the third draw.
Then, as discussed in Example 8.20, by Theorem 8.5
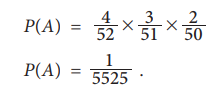
Example 8.20
There are 13 boys and 6 girls in a class. Four students are
selected randomly one after another from that class. Find the probability that:
(i) all are girls, (ii) first two are boys and next are girls
Solution:
i. Suppose that
B: all the randomly selected students are girls
There will be 6 girls among 19 students, in total, while
selecting the first student; there will be 5 girls among 18 students, in total,
while selecting the second student; 4 girls among 17 students, in total, while
selecting the third student; and 3 girls among the remaining 16 students, in
total, while selecting the fourth student.
Then, by applying the Theorem-8.5 for simultaneous occurrence of
these four events, it follows that
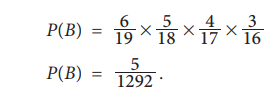
ii. Suppose that
C: In the randomly selected students the first two are boys and
the next are girls
There will be 13 boys among the 19 students, in total, while
selecting the first student; there will be 12 boys among 18 students, in total,
while selecting the second student; 6 girls among 17 students, in total, while
selecting the third student; and 5 girls among the remaining 16 students, in
total, while selecting the fourth student.
Then, by applying the Theorem 8.5 for simultaneous occurrence of
these four events, it follows that
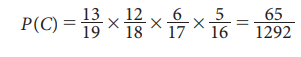
Related Topics