Independent Events

Independent Events

For any two events A and B of a random experiment, if P(A/B) = P(A), then knowledge of the event B does not change the probability for the occurrence of the event A. Such events are called independent events.

If P(A/B) = P(A), then

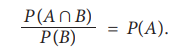
=>  P(A∩B) = P(A) × P(B).

Similarly, the relation P(B/A) = P(B) also indicates the independence of the events A and B.

Definition

 Two events A and B are said to be independent of one another, if

 P(A∩B) = P(A) × P(B).

Example 8.16

In tossing a fair coin twice, let the events A and B be defined as A: getting head on the first toss, B: getting head on the second toss. Prove that A and B are independent events.

Solution:

The sample space of this experiment is

S = {HH, HT, TH, TT}.

The unconditional probabilities of A and B are P(A) = 1/2= P(B).

The event of getting heads in both the tosses is represented by A∩B. The outcome of the experiment in favour of the occurrence of this event is HH. Hence, P(A∩B) = 1/4.

 P(A∩B) = P(A) × P(B) holds. Thus, the events A and B are independent events.

Example 8.17

In the experiment of rolling a pair of dice, the events A, B and C are defined as A : getting 2 on the first die, B : getting 2 on the second die, and C : sum of the faces of dice is an even number. Prove that the events are pair wise independent but not mutually independent?

Solution:

S= { (1,1), (1,2), (1,3), (1,4), (1,5), (1,6),

(2,1), (2,2), (2,3), (2,4), (2,5), (2,6),

(3,1), (3,2), (3,3), (3,4), (3,5), (3,6),

(4,1), (4,2), (4,3), (4,4), (4,5), (4,6),

(5,1), (5,2), (5,3), (5,4), (5,5), (5,6),

(6,1), (6,2), (6,3), (6,4), (6,5), (6,6) }

n(S) = 36

The outcomes which are favourable to the occurrence of these events can be listed below:

A = { (2,1), (2,2), (2,3), (2,4), (2,5), (2,6) }

n(A) = 6

P(A) = 6/36=1/6

B = { (1,2), (2,2), (3,2), (4,2), (5,2), (6,2) }

n(B) = 6

P(B) = 6/36=1/6

C = { (1,1), (1,3), (1,5), (2,2), (2,4), (2,6), (3,1), (3,3), (3,5),

(4,2), (4,4), (4,6), (5,1), (5,3), (5,5), (6,2), (6,4), (6,6) }

n (C) = 18

P(C) = 18/36=1/6

A∩B = { (2,2) }

n(A∩B ) = 1

P(A∩B) = 1/36

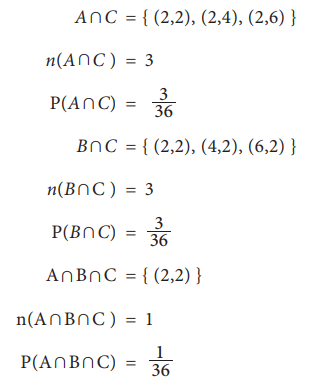
The following relations may be obtained from these probabilities

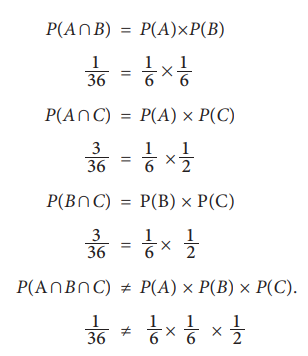
The above relations show that when the events A, B and C are considered in pairs, they are independent. But, when all the three events are considered together, they are not independent.