Definitions of Probability

Definitions of Probability

Probability is a measure of uncertainty. There are three different approaches to define the probability.

Mathematical Probability (Classical / a priori Approach)

If the sample space S, of an experiment is finite with all its elements being equally likely, then the probability for the occurrence of any event, A, of the experiment is defined as

The above definition of probability was used until the introduction of the axiomatic method. Hence, it is also known as classical definition of probability. Since this definition enables to calculate the probability even without conducting the experiment but using the prior knowledge about the experiment, it is also called as a priori probability.

Example 8.5

What is the chance of getting a king in a draw from a pack of 52 cards?

Solution:

In a pack there are 52 cards [n(s) = 52] which is shown in fig. 8.2

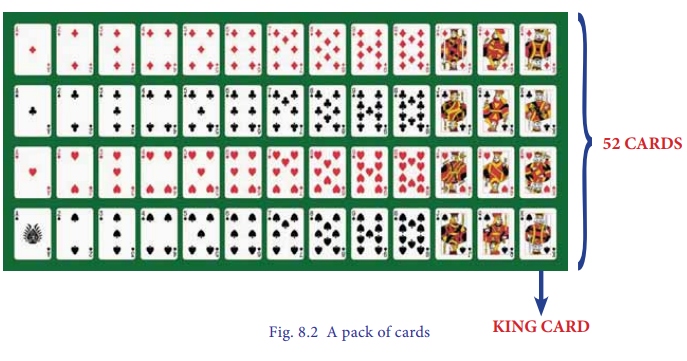
Let A be the event of choosing a card which is a king

In which, number of king cards n(A) = 4

Therefore probability of drawing a card which is king is = P(A) 

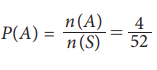
Example 8.6

A bag contains 7 red, 12 blue and 4 green balls. What is the probability that 3 balls drawn are all blue?

Solution:

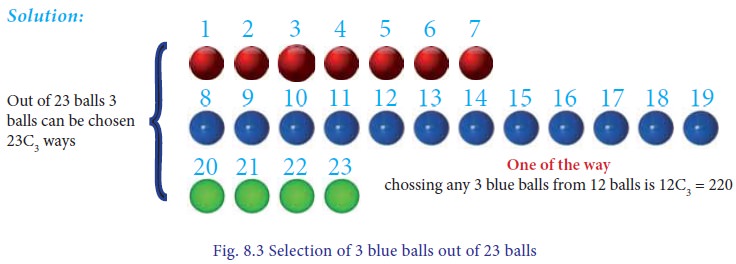
From the fig. 8.3 we find that:

 Total number of balls = 7+12+14=23 balls

 Out of 23 balls 3 balls can be selected in = n(s)= 23C₃ ways

 Let A be the event of choosing 3 balls which is blue

 Number of possible ways of drawing 3 out of 12 blue balls is = n(A)=12C₃ ways

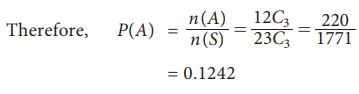
Example 8.7

A class has 12 boys and 4 girls. Suppose 3 students are selected at random from the class. Find the probability that all are boys.

Solution:

From the fig 8.4, we find that:

Total number of students = 12+4=16

Three students can be selected out of 16 students in 16C₃ ways

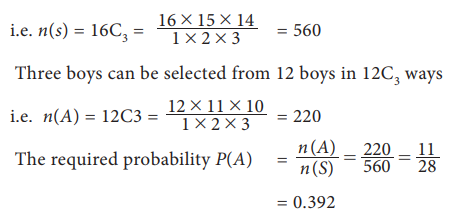
Statistical Probability (Relative Frequency/a posteriori Approach)

If the random experiment is repeated n times under identical conditions and the event A occurred in n(A) times, then the probability for the occurrence of the event A can be defined (Von Mises) as

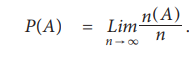
Since computation of probability under this approach is based on the empirical evidences for the occurrence of the event, it is also knows as relative frequency or a posteriori probability.