Conditional Probability

Conditional Probability

Consider the following situations:

i. two events occur successively or one after the other (e.g) A occurs after B has occurred and

ii. both event A and event B occur together.

Example 8.13

There are 4000 people living in a village including 1500 female. Among the people in the village, the age of 1000 people is above 25 years which includes 400 female. Suppose a person is chosen and you are told that the chosen person is a female. What is the probability that her age is above 25 years?

Solution:

Here, the event of interest is selecting a female with age above 25 years. In connection with the occurrence of this event, the following two events must happen.

A:a person selected is female

B:a person chosen is above 25 years.

Situation1:

We are interested in the event B, given that A has occurred. This event can be denoted by B|A. It can be read as “B given A”. It means that first the event A occurs then under that condition, B occurs. Here, we want to find the probability for the occurrence of B|A i.e., P(B|A). This probability is called conditional probability. In reverse, the probability for selecting a female given that a person has been selected with age above 25 years is denoted by P(A|B).

Situation 2:

Suppose that it is interested to select a person who is both female and with age above 25 years. This event can be denoted by A ∩B.

Calculation of probabilities in these situations warrant us to have another theorem namely Multiplication theorem. It is derived based on the definition of conditional probability.

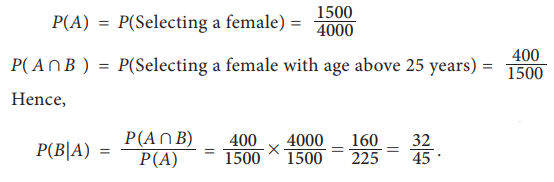
Definition of Conditional of Probability

If P(B) > 0, the conditional probability of A given B is defined as

If P(B) = 0, then P(A∩B) = 0. Hence, the above formula is meaningless when P(B) = 0. Therefore, the conditional probability P(A|B) can be calculated only when P(B)>0.

The need for the computation of conditional probability is described in the following illustration.

Illustration

A family is selected at random from the set of all families in a town with one twin pair. The sample space is

S = {(boy, boy), (boy, girl), (girl, boy), (girl, girl)}.

Define the events

A: the randomly selected family has two boys, and

B: the randomly selected family has a boy.

Let us assume that all the families with one twin pair are equally likely. Since

A = {(boy, boy)},

B = {(boy, boy), (boy, girl), (girl, boy)},

A∩B = A = {(boy, boy)}.

Applying the classical definition of probability, it can be calculated that

Suppose that the randomly selected family has a boy. Then, the probability that the other child in the pair is a girl can be calculated using conditional probability as

Example 8.14

A number is selected randomly from the digits11 through 19. Consider the events

A = { 11,14, 16, 18, 19 }

B = { 12, 14, 18, 19 }

C = { 13, 15, 18, 19 }.

Find (i) P(A/B) (ii) P(A/C) (iii) P(B/C) (iv) P (B/A)

Solution:

Therefore, the probability for the occurrence of A given that B has occurred is

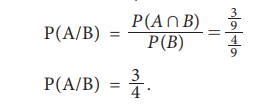
The probability for the occurrence of A given that C has occurred is

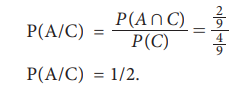
Similarly, the conditional probability of B given C is

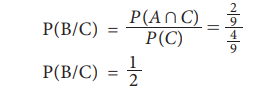
and the conditional probability of B given A is

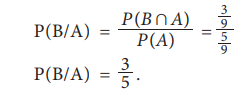
Example 8.15

A pair of dice is rolled and the faces are noted. Let

A: sum of the faces is odd, B: sum of the faces exceeds 8, and

C: the faces are different then find (i) P (A/C) (ii) P (B/C)

Solution:

The outcomes favourable to the occurrence of these events are

A = { (1,2), (1,4), (1,6), (2,1), (2,3), (2,5), (3,2), (3,4), (3,6), (4,1), (4,3), (4,5), (5,2), (5,4), (5,6), (6,1), (6,3), (6,5) }

 B = { (3,6), (4,5), (4,6), (5,4), (5,5), (5,6), (6,3), (6,4), (6,5), (6,6) }

 C = { (1,2), (1,3), (1,4), (1,5), (1,6), (2,1), (2,3), (2,4), (2,5), (2,6), (3,1), (3,2), (3,4), (3,5), (3,6), (4,1), (4,2), (4,3), (4,5), (4,6),  (5,1), (5,2), (5,3), (5,4), (5,6), (6,1), (6,2), (6,3), (6,4), (6,5) }

 Since A and B are proper subsets of C, A∩C = A and B∩C = B.

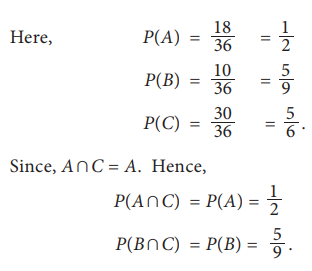
Hence, the probability for the sum of the faces is an odd number given that the faces are different is

Similarly, the probability for the sum of the faces exceeds 8 given that the faces are different is

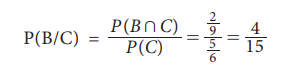
Axioms

The conditional probabilities also satisfy the same axioms introduced in Section 8.3.

If S is the sample space of a random experiment and B is an event in the experiment, then

(i) P(A/B) ≥ 0 for any event A of S.

(ii) P(S/B) = 1

(iii) If A₁, A₂, … is a sequence of mutually exclusive events, then

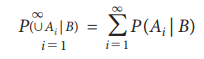
In continuation of conditional probability, another property of events, viz., independence can be studied. It is discussed in the next section. Also, multiplication theorem, a consequence of conditional probability, will be studied later.