Chapter: 11th Statistics : Chapter 8 : Elementary Probability Theory
Addition Theorem of Probability
Addition
Theorem of Probability
Theorem
8.4 : (Addition Theorem of Probability
for Two Events)
If A and B are any two events in a random
experiment, then
P(AŌł¬ B) = P(A) + P(B) ŌĆō
P(AŌł®B)
Proof:
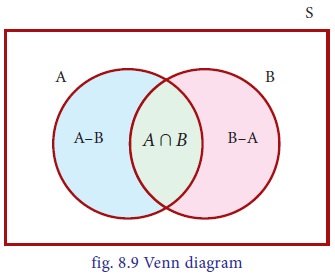
For any
two events A and B, the shaded region in fig. 8.9 represents the event A Ōł¬ B.
AŌł¬ B =AŌł¬(B-(AŌł®B))
The events
A and B-(A Ōł®B) are mutually exclusive.
Using
Axiom 3Ōł¬
P(AŌł¬B) = P(A Ōł¬[B-(A Ōł®B)])
= P(A) +
P[B-(AŌł®B)]
Since(AŌł®B)ŌŖéB,,
B = (A+B)Ōł¬(B ŌĆō(A+B))
The events
on the right hand side are disjoints. Hence by axiom 3
P(B) = P (
A Ōł®B) + P( BŌĆō(AŌł®B))
i.e.
P[BŌĆō(AŌł®B)] = P(B) ŌĆō P(AŌł®B) ŌĆ”ŌĆ”ŌĆ”ŌĆ”..(8.2)
Substituting
(8.2) in (8.1)Ōł¬ it follows that
P(AŌł¬B) = P(A) + P(B) ŌĆō P(AŌł®B).
Corollary: If AŌł¬ B and C are any three events, then
P(AŌł¬ B Ōł¬C) = P(A) + P(B) + P(C) ŌĆō P(AŌł® B) ŌĆō P(AŌł® C) ŌĆō P(BŌł® C) + P(AŌł®BŌł®C)
Example 8.12
In the Annual sports meet, among the 260 students in XI standard
in the school, 90 participated in Kabadi, 120 participated in Hockey, and 50
participated in Kabadi and Hockey. A Student is selected at random. Find the probability
that the student participated in (i) Either Kabadi or Hockey, (ii) Neither of
the two tournaments, (iii) Hockey only, (iv) Kabadi only, (v) Exactly one of
the tournaments.
Solution:
n(s)=260
Let A : the event that
the student participated in Kabadi
B : the event that the
student participated in Hockey.
n(A) = 90; n(B) = 120;
n(AŌł¬B) = 50
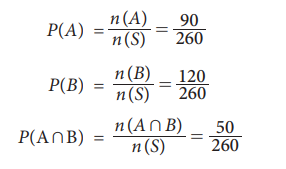
(i) The probability that the student participated in either
Kabadi or Hockey is
P (AŌł¬B) = P(A) + P(B) - P (AŌł®B)
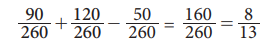
(ii) The probability that the student participated in neither of
the two tournaments in
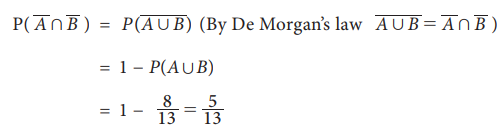
(iii) The probability that the student participated in Hockey
only is
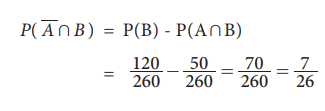
(iv) The probability that the student participated in Kabadi
only

(v) The probability that the student participated in exactly one
of the tournaments is
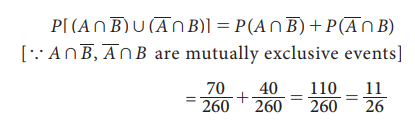
Related Topics