Theorems, Proof, Solved Example Problems - Axioms of Probability | 11th Statistics : Chapter 8 : Elementary Probability Theory
Chapter: 11th Statistics : Chapter 8 : Elementary Probability Theory
Axioms of Probability
Axioms of Probability
Andrey Nikolaevich Kolmogorov (1903–1987) was a 20th-century
Soviet mathematician who made significant contributions to the mathematics of
probability theory, topology, intuitionistic logic, turbulence, classical ...
Wikipedia
A.N. Kolmogorov proposed the axiomatic approach to probability
in 1933. An axiom is a simple, indisputable statement, which is proposed
without proof. New results can be found using axioms, which later become as
theorems.
Axiomatic approach to probability
Let S be the sample
space of a random experiment. If a number P(A) assigned to each event A∈S satisfies the following axioms, then P(A) is called the
probability of A.
Axiom-1 : P (A) ≥ 0
Axiom-2 : P (S) = 1
Axiom-3 : If {A1,A2,…}
is a sequence of mutually exclusive events i.e., Ai ∩ Aj = ϕ
when i ≠j, then
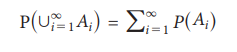
Axiom-3 also holds for a set of finite number of mutually
exclusive events. If A1, A2,…, An are mutually exclusive
events in S and n is a finite positive integer, then
P(A1 ∪ A2 … An) = P(A1) + P(A2)
+ … + P(An).
It may be noted that the previous two approaches to probability
satisfy all the above three axioms.
Basic Theorems of Probability
Theorem 8.1: The probability of
impossible event is 0 i.e., P(Ï•) = 0.
Proof: Let A1 = S and A2 = Ï•. Then, A1 and A2 are mutually
exclusive.
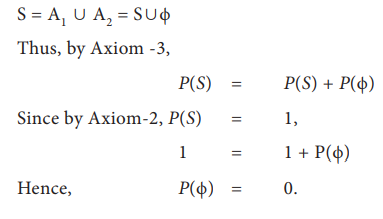
Theorem 8.2: If S is the sample
space and A is any event of the experiment, then
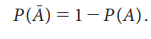
Proof:
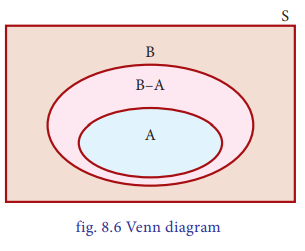
Theorem 8.3: If A and B are
two events in an experiment such that A ⊂B, then P(B-A) = P(B) – P(A).
Proof:
It is given that A ⊂
B.
The event B can be expressed as
B
= A ∪ (B-A)
(see Figure 8.6)
Since A ∩(B-A) = φ,
P(B) = P(A ∪ (B-A))
Hence, by Axiom-3,
=>
P(B) = P(A) + P(B-A)
Therefore, P(B-A) = P(B) – P(A).
Corollary: If A ⊂B,
then P(A)≤ P(B).
Proof:
Since,
by Axiom-1, P(B–A) ≥ 0, it follows that
P(B) – P(A) ≥ 0
P(B) ≥ P(A)
=> P(A) ≤ P(B).
Example 8.8
In
the experiment of tossing an unbiased coin (or synonymously balanced or fair
coin), the sample space is S = {H, T}. What is the probability
of getting head or tail?
Solution :
If
the events A1 and A2 are defined as A1 = {H}
and A2 = {T}, then S = A1 ,A2. Here, the events A1 and A2
are mutually exclusive, because they cannot occur together. Hence, by using
Axiom-3, it can be written as
P(S) = P(A1)+P(A2)
Since the number of elementary events in S in
favour of the occurrence of A1 and A2 is one each, they
have equal chances to occur. Hence, P(A1) = P(A2).
Substituting this, it follows that
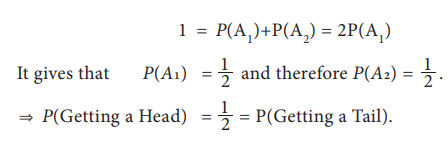
Thus,
a coin is called unbiased, if the probability of getting head is equal to that
of getting tail.
Aliter: (Applying Classical approach)
Example 8.9
Ammu has five toys which are identical and one of them is
underweight. Her sister, Harini, chooses one of these toys at random. Find the
probability for Harini to choose an underweight toy?
Solution :
It is seen from fig. 8.7, the sample space is S = {a1,
a2, a3, a4, a5}.Define the events A1,
A2, A3, A4 and A5 as
A : Harini chooses the underweight toy
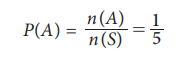
Therefore, the probability for Harini to choose an underweight
toy is 1/5.
Example 8.10
A box contains 3 red and 4 blue socks. Find the probability of
choosing two socks of same colour.
Solution :
From fig. 8.8, total number of socks = 3 + 4 = 7
If two socks are drawn at random, then
No. of ways of selecting 2 socks = 7C2 = 21
then A1 ∪ A2
represents the event of selecting 2 socks of same colour. Since the occurrence
of one event excludes the occurrence of the other, these two events are
mutually exclusive. Then, by Axiom-3,
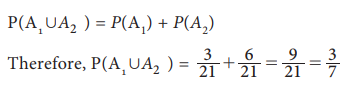
Thus, the probability of selecting two socks of same colour is
3/7.
Example 8.11
Angel selects three cards at random from a pack of 52 cards.
Find the probability of drawing:
i. 3 spade cards.
ii. one spade and two knave cards
iii. one spade, one knave and one heart cards.
Solution:
Total no. of ways of drawing 3 cards = n(S) = 52 C3 =
22100
(a) Let A1 = drawing 3 spade cards.
Since there are 13 Spades cards in a pack of cards,
No. of ways of drawing 3 spade cards = n(A1) = 13 C3
= 286
Therefore, P(A1) =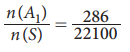 
(b) Let A2 = drawing one spade and two knave cards
No. of ways of drawing one spade card = 13C1 = 13
No. of ways of drawing two knave cards = 13C2= 78
Since drawing a spade and 2 knaves should occur together,
No. of ways drawing one spade and two knave cards = n(A2)
= 13×78 =1014
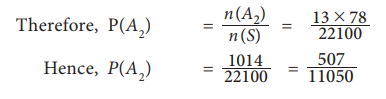
(c) Let A3 = drawing one spade, one knave and one
heart cards
No. of ways of drawing one spade, one knave and one heart cards
is
n(A3) = 13C1× 13C1 × 13C1
= 13 × 13 × 13
Related Topics