Bayes’ Theorem and its Applications

Bayes’ Theorem and its Applications

In some cases, probability for the occurrence of an event of interest A may be difficult to compute from the given information. But, it may be possible to calculate its conditional probabilities P(A/B) and  P(A/) for some other event B of the same experiment. Then, P(A) can be calculated applying the law of total probability. This theorem is a prelude for Bayes’ theorem.

Theorem 8.6 (Law of Total Probability)

In real life situations, decision making is an ongoing process. Situations may arise where we are interested in an event on an ongoing basis. Every time some new information may be available and based on this the probability of the event should be revised. This revision of probability with additional information is formalized in probability theory in the theorem known as Bayes’ Theorem.

Theorem 8.7 (Bayes’ Theorem)

Let B₁, …, B_n be n mutually exclusive events such that where S is the sample space of the random experiment. If P(B_j) > 0 for j = 1, 2, …, n, then for any event A of the same experiment with P(A) > 0,

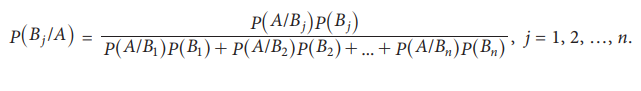
[This Theorem is due to Rev. Thomas Bayes (1701-1761), an English philosopher and a priest. This work was published posthumously by his friend Richard Price during 1763 in the name of Bayes.]

Proof:

For each event B_j, i = 1, 2, … , n, by the definition of conditional probability

Example 8.21

Mr. Arivazhagan, Mr. Ilavarasan and Mr. Anbarasan attended an interview conducted for appointing a Physical Teacher in a school. Mr. Arivazhagan has 45% chance for selection, Mr. Ilavarasan has 28% chance and Mr.Anbarasan has 27% chance. Also, the chance for implementing monthly Mass Drill (MD) programme in the school is 42% if Mr.Arivazhagan is appointed; 40% if Mr.Ilavarasan is appointed; and 48% if Mr.Anbarasan is appointed.

Find the probability that :

i. Mr.Arivazhagan is appointed as the Physical Education Teacher.

ii. Mr.Ilavarasan is appointed as the Physical Education Teacher.

iii. Mr.Anbarasan is appointed as the Physical Education Teacher.

Solution:

Let MD denote the event that the monthly Mass Drill programme is implemented in the school. Also, let

A. Mr.Arivazhagan is appointed

B. Mr.Ilavarasan is appointed

C. Mr.Anbarasan is appointed.S

From fig. 8.10 the information given about these events are

P(A) = 0.45

P(B) = 0.28

P(C) = 0.27

P(MD/A) = 0.42

P(MD/B) = 0.40

P(MD/C) = 0.48

With these, the probability for implementing monthly Mass Drill programme in the school can be computed using total probability as

P(MD) = P(MD/A)P(A)+P(MD/B)P(B)+P(MD/C)P(C)

= (0.42×0.45) + (0.40×0.28) + (0.48×0.27)

= 0.189 + 0.112 + 0.1296

P(MD) = 0.4306.

If it is known that the monthly Mass Drill programme is implemented in the school,

(i) the probability for Mr.Arivazhagan is appointed as the Physical Teacher can be calculated applying Theorem8.7 as

(ii) the probability for Mr.Ilavarasan is appointed as the Physical Teacher can be calculated applying Theorem8.7 as

(iii) the probability for Mr.Anbarasan is appointed as the Physical Teacher can be calculated applying Theorem8.7 as

Example 8.22

Given three identical boxes I, II and III each containing two coins. In box I, both coins are gold coin, in box II, both are silver coins and in the box III, there is one gold and one silver coin. A person chooses a box at random and takes out a coin. If the coin is of gold, what is the probability that the other coin in the box is also of gold.

Solution:

In fig 8.11 given below if yellow colour denotes gold coin and grey colour denotes silver coin then: