Morphology of the Stem

The Stem

The stem is an axial organ of shoot. It has functions of support, transportation, photosynthesis, and storage. Stem has radial structure, no root hairs and grows continuously.

Morphology of the Stem

Stem morphology is simple. Its components are nodes (places where leaves are/were attached) and internodes, long or short (in the last case, plant some-times appears to be stemless, rosette-like).

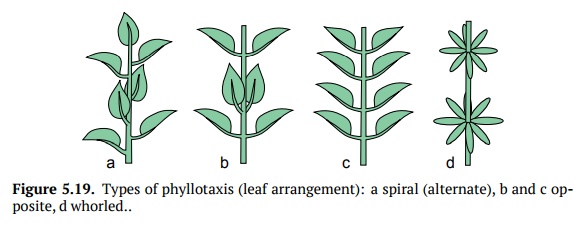
Stems are different by the type of phyllotaxis. The phyllotaxis refers to the arrangement of leaves. If there is one leaf per node, it is a spiral (alternate) ar-rangement. Two leaves per node means opposite arrangement. Opposite leaves can be all in the same plane or each pair can rotate at 90 . If there are more than two leaves per node, it is awhorled arrangement, and each whorl can also rotate.

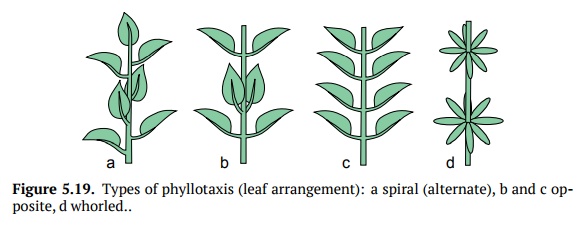
Each type of spiral phyllotaxis has its own angle of divergence. Multiple types of spiral leaf arrangement mostly follow the Fibonacci sequence:

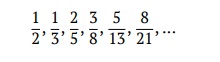
This sequence of numbers made with simple rule: in the every following fraction, the numerator and denominator are sums of two previous numerators and de-nominators, respectively. The sequence looks fairly theoretical but amazingly, it is fully applicable to plant science, namely to different types of spiral phyllotaxis (Fig. 5.20).

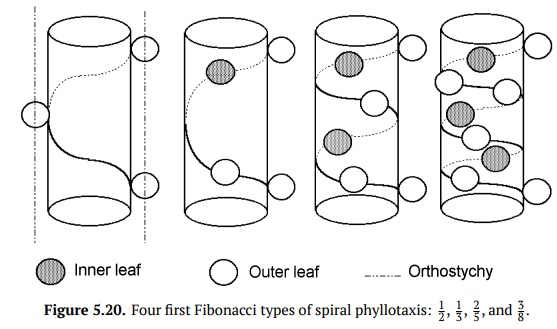
To determine formula of spiral phyllotaxis, one needs to start with arbitrary leaf (or leaf scar) and then find the next (upper) one which is directed the same way, lays on the same virtual line, orthostychy. Then, the imaginary spiral should be drawn trough basements from the started leaf to the corresponding upper leaf. This spiral should go through all intermediary leaves, there might be one, two or more intermediary leaves. Also, the spiral will go at least one time around the stem. (Instead of the imaginary spiral, it is sensible to use a thin thread). One needs to count all leaves in the spiral except the first, and also count number of rotations. The number of leaves counted will be the denominator of the formula, and the number of rotations is the numerator. This is how Fibonacci numbers appear in plant morphology.

These phyllotaxis formulas are relatively stable and sometimes even taxon-specific. For example, grasses (Gramineae) have 1/2 phyllotaxis, sedges (Carex) 1/3, many Rosaceae (like apple, Malus or cherry, Prunus) have 2/5, willows frequently have 3/8, et cetera.

It is still not absolutely clear why the spiral phyllotaxis is under such a theoret-ical mathematical rule. The most feasible hypothesis emphasizes the competition between leaf primordia around SAM.