MerkleHellman Knapsacks

MerkleHellman Knapsacks

Merkle and Hellman [MER78b] developed an encryption algorithm based on the knapsack problem described earlier. The knapsack problem presents a set of positive integers and a target sum, with the goal of finding a subset of the integers that sum to the target. The knapsack problem is NP-complete, implying that to solve it probably requires time exponential in the size of the problemin this case, the number of integers.

We present MerkleHellman in two steps, to aid understanding. First we outline the operation of the MerkleHellman knapsack encryption method. Then we revisit the technique in more detail.

Introduction to MerkleHellman Knapsacks

The idea behind the MerkleHellman knapsack scheme is to encode a binary message as a solution to a knapsack problem, reducing the ciphertext to the target sum obtained by adding terms corresponding to 1s in the plaintext. That is, we convert blocks of plaintext to a knapsack sum by adding into the sum those terms that match with 1 bits in the plaintext, as shown in Figure 12-14.

A knapsack is represented as a vector of integer terms in which the order of the terms is important. There are actually two knapsacksan easy one, to which a fast (linear time) algorithm exists, and a hard one, derived by modifying the elements of the easy knapsack. The modification is such that a solution with the elements of either knapsack is a solution for the other one as well. This modification is a trapdoor, permitting legitimate users to solve the problem simply. Thus, the general problem is NP-complete, but a restricted version of it has a very fast solution.

The algorithm begins with a knapsack set, each of whose elements is larger than the sum of all previous elements. Suppose we have a sequence where each element a_k is larger than a₁ + a₂ +…+ a_k-1. If a sum is between a_k and a_k+1, it must contain a_k as a term, because no combination of the values a₁, a₂,…, a_k-1 could produce a total as large as a_k. Similarly, if a sum is less than a_k, clearly it cannot contain a_k as a term.

The modification of the algorithm disguises the elements of the easy knapsack set by changing this increasing -size property in a way that preserves the underlying solution. The modification is accomplished with multiplication by a constant mod n.

Detailed Explanation of the MerkleHellman Technique

This detailed explanation of MerkleHellman is intended for people who want a deeper understanding of the algorithm.

General Knapsacks

The knapsack problem examines a sequence a₁, a₂, …, a_n of integers and a target sum, T. The problem is to find a vector of 0s and 1s such that the sum of the integers associated with 1s equals T. That is, given S = [a₁,a₂, …, a_n], and T, find a vector V of 0s and 1s such that

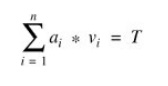
For example, consider the list of integers [17,38,73,4,11,1] and the target number 53. The problem is to find which of the integers to select for the sum, that is, which should correspond with 1s in V. Clearly 73 cannot be a term, so we can ignore it. Trying 17, the problem reduces to finding a sum for (53 - 17 = 36). With a second target of 36, 38 cannot contribute, and 4 + 11 + 1 are not enough to make 36. We then conclude that 17 is not a term in the solution.

If 38 is in the solution, then the problem reduces to the new target (53 - 38 = 15). With this target, a quick glance at the remaining values shows that 4 and 11 complete the solution, since 4 + 11 = 15. A solution is thus 38 + 4 + 11.

This solution proceeded in an orderly manner. We considered each integer as possibly contributing to the sum, and we reduced the problem correspondingly. When one solution did not produce the desired sum, we backed up, discarding recent guesses and trying alternatives. This backtracking seriously impaired the speed of solution.

With only six integers, it did not take long to determine the solution. Fortunately, we discarded one of the integers (73) immediately as too large, and in a subproblem we could dismiss another integer (38) immediately. With many integers, it would have been much more difficult to find a solution, especially if they were all of similar magnitude so that we could not dismiss any immediately.

Superincreasing Knapsacks

Suppose we place an additional restriction on the problem: The integers of S must form a superincreasing sequence, that is, one where each integer is greater than the sum of all preceding integers. Then, every integer a_k would be of the form

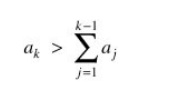
In the previous example, [1,4,11,17,38,73] is a superincreasing sequence. If we restrict the knapsack problem to superincreasing sequences, we can easily tell whether a term is included in the sum or not. No combination of terms less than a particular term can yield a sum as large as the term. For instance, 17 is greater than 1 + 4 + 11 (=16). If a target sum is greater than or equal to 17, then 17 or some larger term must be a term in the solution.

The solution of a superincreasing knapsack (also called a simple knapsack) is easy to find. Start with T. Compare the largest integer in S to it. If this integer is larger than T, it is not in the sum, so let the corresponding position in V be 0. If the largest integer is less than or equal to T, that integer is in the sum, so let the corresponding position in V be 1 and reduce T by the integer. Repeat for all remaining integers in S.

An example solving a simple knapsack for targets 96 and 95 is shown in Figure 12-15.

The Knapsack Problem as a Public Key Cryptographic Algorithm

The MerkleHellman encryption technique is a public key cryptosystem. That is, each user has a public key, which can be distributed to anyone, and a private key, which is kept secret. The public key is the set of integers of a knapsack problem (not a superincreasing knapsack); the private key is a corresponding superincreasing knapsack. The contribution of Merkle and Hellman was the design of a technique for converting a superincreasing knapsack into a regular one. The trick is to change the numbers in a nonobvious but reversible way.

Modular Arithmetic and Knapsacks

In normal arithmetic, adding to or multiplying a superincreasing sequence preserves its superincreasing nature, so the result is still a superincreasing sequence. That is, if a > b then k * a > k * b for any positive integer k.

However, in arithmetic mod n, the product of two large numbers may in fact be smaller than the product of two small numbers, since results larger than n are reduced to between 0 and n-1. Thus, the superincreasing property of a sequence may be destroyed by multiplication by a constant mod n.

To see why, consider a system mod 11. The product 3 * 7 mod 11 = 21 mod 11 = 10, while 3 * 8 mod 11 = 24 mod 11 = 2. Thus, even though 7 < 8, we find that 3 * 7 mod 11 > 3 * 8 mod 11. Multiplying a sequence of integers mod some base may destroy the superincreasing nature of the sequence.

Modular arithmetic is sensitive to common factors. If all products of all integers are mapped into the space of the integers mod n, clearly there will be some duplicates; that is, two different products can produce the same result mod n. For example, if w * x mod n = r, then w * x + n mod n = r, w * x + 2n mod n = r, and so on. Furthermore, if w and n have a factor in common, then not every integer between 0 and n-1 will be a result of w * x mod n for some x.

For instance, look at the integers mod 5. If w = 3 and x = 1, 2, 3,…, the multiplication of x * w mod 5 produces all the results from 0 to 4, as shown in Table 12-13. Notice that after x = 5, the modular results repeat.

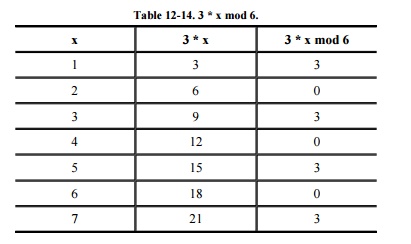
However, if we choose w = 3 and n = 6, not every integer between 0 and 5 is used. This occurs because w and n share the common factor 3. Table 12-14 shows the results of 3 * x mod 6. Thus, there may be some values that cannot be written as the product of two integers mod n for certain values of n. For all values between 0 and n-1 to be produced, n must be relatively prime to w (that is, they share no common factors with each other).

If w and n are relatively prime, w has a multiplicative inverse mod n. That means that for every integer w, there is another integer w^-1 such that w * w^-1 = 1 mod n. A multiplicative inverse undoes the effect of multiplication: (w * q) * w^{- 1} = q. (Remember that multiplication is commutative and associative in the group mod n, so that w * q * w^-1 = (w * w^-1) * q = q mod n.)

With these results from modular arithmetic, Merkle and Hellman found a way to break the superincreasing nature of a sequence of integers. We can break the pattern by multiplying all integers by a constant w and taking the result mod n where w and n are relatively prime.

Transforming a Superincreasing Knapsack

To perform an encryption using the MerkleHellman algorithm, we need a superincreasing knapsack that we can transform into what is called a hard knapsack. In this section we show you just how to do that.

We begin by picking a superincreasing sequence S of m integers. Such a sequence is easy to find. Select an initial integer (probably a relatively small one). Choose the next integer to be larger than the first. Then select an integer larger than the sum of the first two. Continue this process by choosing new integers larger than the sum of all integers already selected.

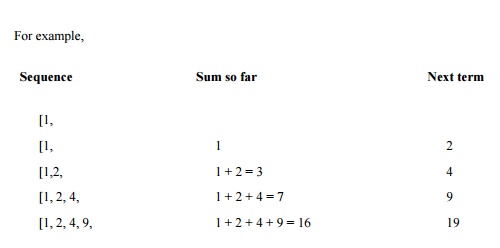
is such a sequence.

The superincreasing sequence just selected is called a simple knapsack. Any instance of the knapsack problem formed from that knapsack has a solution that is easy to find.

After selecting a simple knapsack S = [s₁, s₂,…,s_m], we choose a multiplier w and a modulus n. The modulus should be a number greater than the sum of all s_i. The multiplier should have no common factors with the modulus. One easy way to guarantee this property is to choose a modulus that is a prime number, since no number smaller than it will have any common factors with it.

Finally, we replace every integer s_i in the simple knapsack with the term

h_i = w * s_i mod n

Then, H = [h₁, h₂,…, h_m] is a hard knapsack. We use both the hard and simple knapsacks in the encryption.

For example, start with the superincreasing knapsack S = [1, 2, 4, 9] and transform it by multiplying by w and reducing mod n where w = 15 and n = 17.

1 * 15 = 15 mod 17 = 15

2 * 15 = 30 mod 17 = 13

4 * 15 = 60 mod 17 = 9

9 * 15 = 135 mod 17 = 16

The hard knapsack derived in this example is H = [15, 13, 9, 16].

Example Using MerkleHellman Knapsacks

Let us look at how to use MerkleHellman encryption on a plaintext message P. The encryption algorithm using MerkleHellman knapsacks begins with a binary message. That is, the message is envisioned as a binary sequence P = [p₁, p₂,…, p_k]. Divide the message into blocks

of m bits, P₀ = [p_l, p₂,…, p_m], P₁ = [p_m+1,…, p_2m], and so forth. The value of m is the number of terms in the simple or hard knapsack.

The encipherment of message P is a sequence of targets, where each target is the sum of some of the terms of the hard knapsack H. The terms selected are those corresponding to 1 bits in P_i so that P_i serves as a selection vector for the elements of H. Each term of the

ciphertext is P_i * H, the target derived using block P_i as the selection vector.

For this example, we use the knapsacks S = [1, 2, 4, 9] and H = [15, 13, 9, 16] obtained in the previous section. With those knapsacks, w = 15, n = 17, and m = 4. The public key (knapsack) is H, while S is kept secret.

The message

P = 0100101110100101

is encoded with the knapsack H = [15, 13, 9,16] as follows.

P = 0100 1011 1010 0101

[0, 1, 0, 0] * [15, 13, 9, 16] = 13 [1, 0, 1, 1] * [15, 13, 9, 16] = 40 [1, 0, 1, 0] * [15, 13, 9, 16] = 24 [0, 1, 0, 1] * [15, 13, 9, 16] = 40

The message is encrypted as the integers 13, 40, 24, 29, using the public knapsack H = [15, 13, 9, 16].

Knapsack Decryption Algorithm

The legitimate recipient knows the simple knapsack and the values of w and n that transformed it to a hard public knapsack. The legitimate

recipient determines the value w^-1 so that w * w^-1 = 1 mod n. In our example, 15 * 1 mod 17 is 8, since 15 * 8 mod 17 = 120 mod 17 = (17 * 7) + 1 mod 17 = 1.

Remember that H is the hard knapsack derived from the simple knapsack S. H is obtained from S by 

H = w * S mod n

 (This notation, in which a constant is multiplied by a sequence, should be interpreted as hi = w * si mod n for all i, 1 i m.)

The ciphertext message produced by the encryption algorithm is

C = H * P = w * s * P mod n

To decipher, multiply C by w^-1, since

w^-1 * C = w^-1 * H * P = w^-1 * w * S * P = S * P mod n

To recover the plaintext message P, the legitimate recipient would solve the simple knapsack problem with knapsack S and target w^-1 * C_i for each ciphertext integer C_i. Since w^-1 * C_i = S * P mod n, the solution for target w^-1 * C_i is plaintext block P_i, which is the message originally encrypted.

Example of Decryption

We continue our example, in which the underlying simple knapsack was S = [1, 2, 4, 9], with w = 15 and n = 17. The transmitted messages were 13, 40, 24, and 29.

To decipher, we multiply these messages by 8 mod 17 because 8 is 15^-1 mod 17. Then we can easily solve the simple knapsacks, as shown here:

13 * 8 = 104 mod 17 = 2 = [0100] 40 * 8 = 320 mod 17 = 14 = [1011]

24 * 8 = 192 mod 17 = 5 = [1010] 29 * 8 = 232 mod 17 = 11 = [0101]

The recovered message is thus 0100101110100101.

Cryptanalysis of the Knapsack Algorithm

In this example, because m is 4, we can readily determine the solution to the knapsack problem for 13, 40, 24, and 29. Longer knapsacks (larger values of m), which also imply larger values of the modulus n, are not so simple to solve.

Typically, you want to choose the value of n to be 100 to 200 binary digits long. If n is 200 bits long, the s_i are usually chosen to be about

2²⁰⁰ apart. That is, there are about 200 terms in the knapsacks, and each term of the simple knapsack is between 200 and 400 binary digits long. More precisely, s₀ is chosen so that

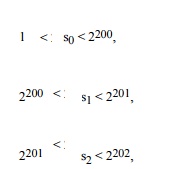
and so on, so that there are approximately 2²⁰⁰ choices for each s_i.

You can use a sequence of m random numbers, r₁, r₂, r₃,…, r_m to generate the simple knapsack just described. Each r_i must be between 0 and 2²⁰⁰. Then each value s_i of the simple knapsack is determined as

s_i = 2^200+i-1 + r_i

for i = 1, 2,…, m.

With such large terms for S (and H), it is infeasible to try all possible values of s_i to infer S given H and C. Even assuming a machine could do one operation every microsecond, it would still take 10⁴⁷ years to try every one of the 2²⁰⁰ choices for each s_i. A massively parallel machine with 1000 or even 1,000,000 parallel elements would not reduce this work factor enough to weaken the encryption.

Weaknesses of the MerkleHellman Encryption Algorithm

The MerkleHellman knapsack method seems secure. With appropriately large values for n and m, the chances of someone's being able to crack the method by brute force attack are slim.

However, an interceptor does not have to solve the basic knapsack problem to break the encryption, since the encryption depends on specially selected instances of the problem. In 1980, Shamir found that if the value of the modulus n is known, it may be possible to determine the simple knapsack. The exact method is beyond the scope of this book, but we can outline the method of attack. For more information, see the articles by Shamir and Zippel [SHA80] and Adleman [ADL83].

First, notice that since all elements of the hard knapsack are known, you can readily determine which elements correspond to which elements of the simple knapsack. Consider h₀ and h₁, the first two elements of a hard knapsack, corresponding to simple knapsack

elements s₀ and s₁.

Let

ρ= h₀/h₁ mod n

Since h₀ = w * s₀ mod n and h₁ = w * s₁ mod n, it is also true that

ρ = (w * s₀)/(w * s₁) = s₀/s₁ mod n

Given the ratio ρ, determine the sequence

= ρ mod n, 2 * ρ mod n 3 * ρ mod n, …, k * ρ mod n, …, 2m * ρ mod n

For some k, k and sl will cancel each other mod n; that is, k * (1/s1) = 1 mod n. Then

k * ρ mod n = k * s0 * 1/s1 mod n = so mod n = s0                        

It is reasonable to expect that s         0        will be the smallest element of . Once s       0        is known, determining w, then w-1 and each of the s are not

                                                i

hard.

A more serious flaw was identified later by Shamir [SHA82] . The actual argument is also beyond the scope of this book, but again it can be sketched fairly briefly. The approach tries to deduce w and n from the hi alone.

The approximate size of n can be deduced from the fact that it will be longer than any of the hi since they have been reduced mod n; however, n will not be substantially longer than the longest hi, since it is likely that the results after taking the modulus will be fairly evenly distributed between 1 and n.

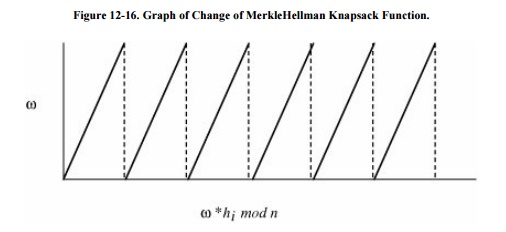
Assume you are trying to guess w. You might iteratively try different candidate values ω= 1, 2, 3, . . . for w. The graph of ω * hi mod n as a function of ω would increase steadily until a value of ω * hi was greater than n. At that point, the graph of ω * hi would be discontinuous and have a small value. The values of ω * hi would then resume their steady increase as ω increased until ω * hi exceeded n again. The graph would form a progression of jagged peaks, resembling the teeth of a saw. The slope of each "tooth" of the graph is hi. Figure 12-16 displays a graphical representation of this process.

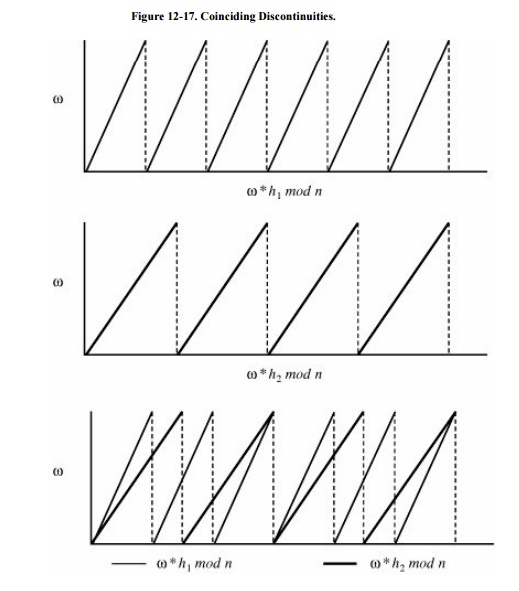
The correct value of ω = w occurs at one of the points of discontinuity of the graph of ω * h_i mod n. This same pattern occurs for all values h_i: h₁, h₂, and so forth. Since ω is a discontinuity point of ω * h₁ mod n, it is also a discontinuity of ω * h₂ mod n, of ω * h₃ mod n, and so forth. To determine ω superimpose the graph of ω * h₁ mod n on ω * h₂ mod n, superimpose those graphs on ω * h₃ mod n, and so on.

Then, w will be at one of the places where all of the curves are discontinuous and fall from a high value to a low one. Two such graphs are shown in Figure 12-17. The problem of determining w is thus reduced to finding the point at which all of these discontinuities coincide.

The actual process is a little more difficult. The value of n has been replaced by real number N. Since n and N are unknown, the graphs are scaled by dividing by N and then approximating by successive values of the real number ω/N in the function (ω/N) * h_i mod 1.0.

Fortunately, this reduces to the solution of a system of simultaneous linear inequalities. That problem can be solved in polynomial time. Therefore, the Merkle Hellman knapsack problem can be broken in reasonable time.

Notice that this solution does not apply to the general knapsack problem; it applies only to the special class of knapsack problems derived from superincreasing sequences by multiplication by a constant modulo another constant. Thus, the basic knapsack problem is intact; only this restricted form has been solved. This result underscores the point that a cryptosystem based on a hard problem is not necessarily as hard to break as the underlying problem.

Since it has become known that the MerkleHellman knapsack can be broken, other workers have analyzed variations of MerkleHellman knapsacks. (See, for example, [BRI83] and [LAG83].) To date, transformed knapsacks do not seem secure enough for an application where a concerted attack can be expected. The MerkleHellman algorithm or a variation would suffice for certain low-risk applications. However, because the MerkleHellman method is fairly complicated to use, it is not often recommended.