Advanced Encryption Standard

The simple design leads to a fast and easy implementation.

Serpent by Anderson et al. [AND98b]. This algorithm is cryptographically conservative, meaning that it has been structured with more rounds of confusion and diffusion than its designers think are necessary. It uses 32 rounds, each of which consists of a key addition, 4-bit to 4-bit substitution using one of eight substitutions, and then some mixing operations that combine bits across different 32-bit words. The algorithm lends itself readily to hardware (chip) implementation, based on parallel 4-bit subprocessors.

Twofish from Counterpane Security [SCH98]. The designers of Twofish developed a design of substitution tables that depends on the encryption key instead of on fixed substitution tables (like the S-boxes of DES). This approach, the designers state, leads to greater security. As in DES, the algorithm operates on half the block at a time and then the two halves are swapped. Each round involves matrix multiplication in a finite field. Some of Twofish's work can be precomputed, so the implementation can be optimized for speed.

Rijndael by Daemen and Rijmen [DAE00, DAE02]. This algorithm uses cycles of four different kinds of operations, although all of the operations are simple. Thus, the implementation should be simple and efficient, without a significant sacrifice to security.

NIST indicated that no cryptographic weaknesses had been found in any of the five candidate algorithms. Rijndael was selected because it offered the best combination of security, performance, efficiency, ease of implementation, and flexibility. In 2001 it was formally adopted by the U.S. government for protection of government data transmission and storage. NIST relied heavily on public analysis of the algorithms.

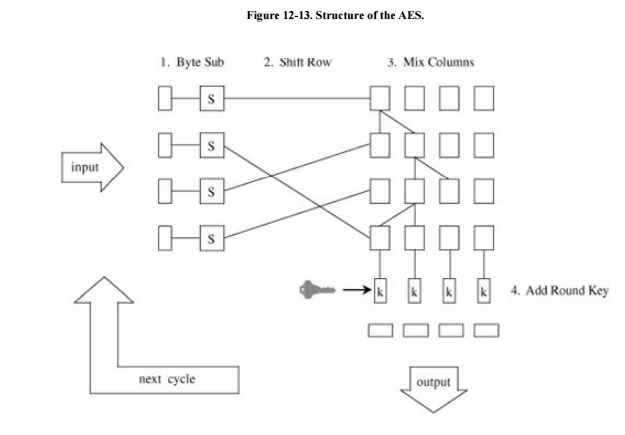
Structure of the AES

AES is a block cipher of block size 128 bits. The key length can be 128, 192, or 256 bits. (Actually, the Rijndael algorithm can be extended to any key length that is a multiple of 64, although only 128, 192, and 256 are recognized in the AES standard.)

AES is a substitution-permutation cipher involving n rounds, where n depends on the key length. For key length 128, 10 rounds are used; for 192, 12; and for 256, 14. The cycle of AES is simple, involving a substitution, two permuting functions, and a keying function.

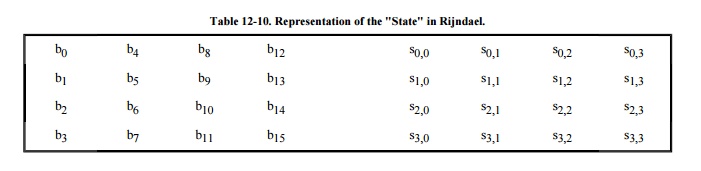
It is convenient to think of a 128 -bit block of AES as a 4 x 4 matrix, called the "state." We present the state here as the matrix s[0,0]..s[3,3]. The state is filled from the input in columns. Assume, for example, that the input is the 16 bytes b₀, b₁, b₂, b₃,..., b₁₅. These bytes are then

represented in the state as shown in Table 12-10. Some operations in Rijndael are performed on columns of the state, and some on rows, so this representation implements a form of columnar transposition.

The four steps of the algorithm operate as follows.

           Byte substitution: The first step is a simple substitution: s[i,j] becomes s'[i,j], through a defined substitution table.

           Shift row: In the second step, the rows of s are permuted by left circular shift; the first (leftmost, high order) i elements of row i are shifted around to the end (rightmost, low order).

           Mix columns: The third step is a complex transformation on the columns of s under which the four elements of each column are multiplied by a polynomial, essentially diffusing each element of the column over all four elements of that column.

           Add round key: Finally, a key is derived and added to each column.

This sequence is repeated for a number of rounds depending on the key length.

Before describing these rounds, we must first mention that Rijndael is defined in the Galois field GF(2⁸) by the irreducible polynomial

p = x⁸ + x⁴ + x³ + x + 1

In this mathematical system, a number is represented as a series of coefficients to this eighth-degree polynomial. For example, the number 23, represented in binary as 10111, is the polynomial

1x⁴ + 0x³ + 1x² + 1x + 1 = x⁴ + x² + x¹ + 1

Addition of coefficients is performed (mod 2), so that addition is the same as subtraction which is the same as exclusive OR: 0 + 0 = 0, 1 + 0 = 0 + 1 = 1, 1 + 1 = 0. Multiplication is performed as on polynomials: (x³ + 1) * (x⁴ + x) = (x⁷ + x⁴ + x⁴ + x) = (x⁷ + x).

Although the mathematics of Galois fields are well beyond the scope of this book, it is important to realize that this mathematical foundation adds an underlying structure to what might otherwise seem like the random scrambling of numbers. As we explain how Rijndael works, we point out the uses of the Galois field, without necessarily explaining their full meaning. The mathematical underpinning gives credibility to Rijndael as a strong cipher.

Byte Substitution

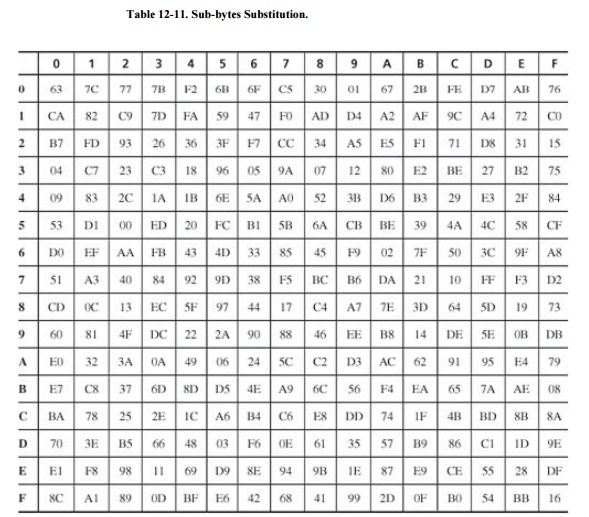
Rijndael byte substitution is a conventional substitution box. However, the designers opened a small window into their algorithm's structure. The table is not just an arbitrary arrangement of bytes. Each byte b is replaced by the byte which is the result of the following two mathematical steps:

           Compute the multiplicative inverse of b in GF(2⁸); 0, having no multiplicative inverse, is represented by 0.

           Exclusive OR that result with 99 = hexadecimal 63 = 0110 0011.

Using inverses in GF(2⁸) ensures that each value appears exactly once in the table. Combining with 99 helps break up patterns. The complete substitution table is shown in Table 12-11. For example, the byte 20 is replaced by B7, in row 2, column 0.

Shift Row

Actually, Rijndael is defined for blocks of size 128, 192, and 256 bits, too, even though the AES specifies a block size of only 128 bits. In the shift row step, assume a block is composed of 16 (or 24 or 32) bytes numbered (from left, or most significant, to right) 1 to 16 (or 24 or 32). In the shift row, the numbered bytes are shifted to the positions as shown in Table 12-12. That is, for 128- and 192-bit blocks, row i is rotated left (i-1) bytes; for 256-byte blocks, rows 3 and 4 are shifted an extra byte.

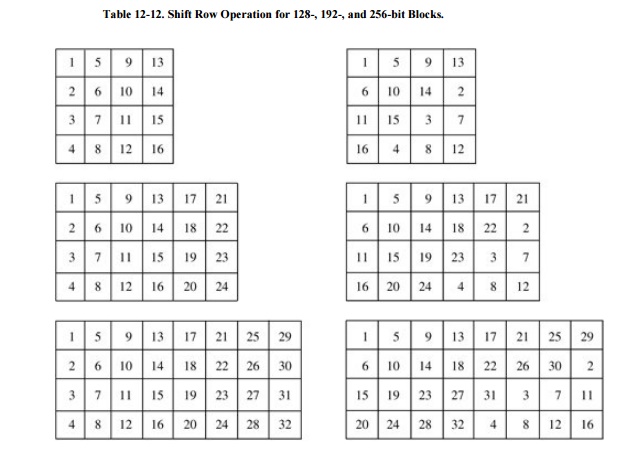
That is, row n is shifted left circular (n-1) bytes, except for 256-bit blocks, in which case row 2 is shifted 1 byte and rows 3 and 4 are shifted 3 and 4 bytes, respectively.

Mix Column

In the mix column operation, each column (as depicted in shift rows) is multiplied by the matrix

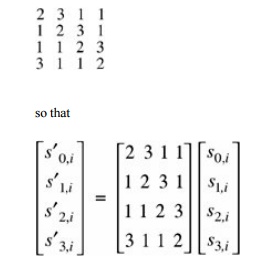
However, this "multiplication" is performed on bytes by logical operations, so multiplying the column by 1 means leaving it unchanged, multiplying by 2 (binary 10) means shifting each byte left one bit, and multiplying by 3 (binary 11) means shifting left one bit and adding (exclusive ORing) the original unshifted value. 

Add Subkey

The final step of a cycle is to add (exclusive OR) a variation of the key with the result so far. The variation is as follows. The first key is the key itself. The second key is changed 4-byte word by word. The first word is rotated one byte left, then transformed by the substitution of the byte substitution step, then added (exclusive ORed) with a constant. The rest of the words in that subkey are produced by the exclusive OR of the first word with the corresponding word from the previous key. So, if key variation k₁ is w₁w₂w₃w₄ (four 32-bit words, or 128 bits), then k2 is w1'(w2 w1')(w3 w1')(w4 w1') where w1'is w1 rotated left 1 byte, substituted, and exclusive ORed with a constant.

A picture of the full AES is shown in Figure 12-13. Notice that in the Mix Columns step the algorithm takes a "right turn," changing from a row (word) orientation to a column structure.

Cryptanalysis of the AES

Rijndael has been subjected to extensive cryptanalysis by professional and amateur cryptographers since it was proposed for the AES. It is a variation on an earlier algorithm, Square, from the same authors; that algorithm, too has been analyzed extensively in the community.

To date, no significant problems have been found with Rijndael. One property that has been discovered, which is both good and bad, is that it is quite regular. Regularity is evident if an input is chosen and all bytes except one of that input are held constant. Then, the one remaining byte is repeatedly changed through all 256 different possible values; after one round of Rijndael, 4 bytes will go through all 256 values, and after two rounds, 16 bytes will go through all 256 values. This result demonstrates unusually good diffusion, in that small changes in the input have a widespread effect. However, the regularity of this pattern might give some clue to an attacker, although that is unlikely.

We have noted that Rijndael draws heavily from algebra, especially Galois fields. The substitution and column mixing functions are not just numbers chosen at random but instead solve certain fundamental problems in Galois field theory. The authors have not offered a mathematical argument for why such a basis gives strength toor at least does not detract fromthe approach. But substantial work in that area makes it unlikely that there are any hidden shortcutsways in which an attacker could solve an encryption in a manner significantly easier than a brute force key search. Over time we can expect mathematicians to explore this algorithm and its underlying field.

For now, the AES seems a solid replacement for the DES.

RC2, RC4, and RC5

The RC2, RC4 and RC5 ciphers all come from Ron Rivest, one of the inventors of the RSA algorithm and founder of RSA Laboratories. The RC in the names means either "Rivest cipher" or "Ron's code," depending on which source you believe. The ciphers are structurally different, but all have some degree of common use, so we explore them briefly here.

RC2

RC2 is a block cipher designed as a simple and fast algorithm [KNU02]. Although Rivest originally intended the algorithm to be held proprietary, someone released its design description on the Internet in 1996. The algorithm was first intended for international use by the Lotus Notes office application suite; it would use a short enough key (40 bits) to satisfy U.S. export restrictions to most countries, thereby assuring Lotus of international marketablity. In fact, RC2 supports key sizes from 8 to 128 bits, giving it strength exceeding DES against exhaustive key search. Its operation is similar enough to DES that it can be substituted for DES in applications, giving an international edition with no difficulty. With relaxation of export restrictions in 2000, the need for a shorter-key DES replacement has fallen.

RC2 consists of two operations: mixing and mashing. In mixing, a bit stream undergoes some transposition in the form of bit shifting with concurrent substitution through binary (AND, OR, NOT) operations on parts of the bits. During each round of mixing, a complete shuffle of bits occurs from right, moving left, and cycling around to the right again. There are sixteen rounds of mixing. The mashing round is pure substitution. Two mashing rounds are performed after mixing rounds 5 and 11.

Invented in 1987, RC2 is old as cryptosystems go. There have been no serious weaknesses discovered in the design.

RC4

RC4 is a stream cipher, widely used in wireless networks (WEP and WPA), as well as in SSL and various products. It was especially popular before 2000 because, like RC2, it employs a variable length key and so could be configured to use a 40-bit key, short enough to pass export restrictions.

RC4 is essentially a keyed pseudorandom number generator (PRNG); it generates a stream of bits in no predictable order. For encryption, the stream of bits is XORed with the plaintext bits.

The algorithm is ingeniously simple. It uses a 256-element array A containing each of the 256 possible values of an 8-bit byte. Pointers i and j identify bytes from the array to be swapped. At each step, i is incremented by 1, j is replaced by j + A[i], A[i] and A[j] are swapped, and the byte A[A[i]+A[j]] is produced as output. (All additions are carried out mod 256.) The algorithm is very efficient, especially for a software implementation.

No serious cryptanalytic weaknesses have been found in the algorithm itself. However, as noted in Chapter 2, the random number sequence of an XOR stream cipher must never repeat. That is, the same key must never be used for two different plaintexts. To see why, consider plaintexts p₁ and p ₂, encrypted with a common key k.

from which p₁ and p₂ may be recoverable with frequency analysis, probable plaintext, or other techniques.

Many implementations of RC4 have exactly that weakness. To initialize array A, the algorithm starts with all 256 bytes in numerical order.

Then it works through the 256 bytes, swapping each byte with a byte whose location depends, in part, on a byte from the key: for each i,

j := j + A[i] + key[i]

and A[i] and A[j] are swapped. So the up-to-256-byte key controls how the random number array is initialized.

To protect against identical plaintext attacks, ciphers, especially XOR stream ciphers, are used with an initialization vector, also called a nonce. In some implementations of RC4 the nonce is appended to the key, effectively extending and randomizing the key.

Fluhrer et al. [FLU01] analyzed the output of RC4 for all possible keys and found that the output is biased, leaking information about the key. If the nonce has been appended to the key, it is possible to narrow the search space for the key significantly.

RC4 is widely used for WEP encryption on wireless networks. The wireless access point and remote device use the same key indefinitely until manually rekeyed. The weakness Fluhrer et al. identified has allowed WEP encryption to be broken in minutes. This weakness has led to the development of WPA and WPA2 for wireless communication, the latter using the much stronger AES encryption.

RC4 has also been used in Microsoft Office products Word and Excel to encrypt password-protected documents. Microsoft makes the mistake of encrypting each version of a document under the same encryption key (password). Wu [WU05] describes an attack like the XOR stream attack described above by which the text of an encrypted document can be retrieved easily given two versions of the document.

RC5

RC5 is a fully parameterized block cipher; this means the key length, block size, and number of cycles can be varied to alter the balance between security and complexity of operation and use. RC5 [RIV94] uses a simple design that served as a model for the AES candidate RC6.

A data block in RC5 is split in half, the left half is modified, the halves are swapped, the new left half (that is, the old right half) is modified the same way, and the halves are swapped again. That sequence constitutes a full round of the algorithm. The modifications of each half - round involve XOR, circular shift, and addition of a portion of the key. In an unusual twist for a cryptographic algorithm, the number of bits shifted depends on the input data: The left half is shifted by the number of bits of the value of the right half.

No significant weaknesses have been found in RC5. Encryption with a small number of rounds (12) has been found to be subject to differential cryptanalysis, but the number of rounds can be set arbitrarily. Because the operations per round are few and simple and the speed of the implementation depends linearly on the number of rounds, raising the number of rounds above 12 does not significantly slow down encryption.

Cryptographic Challenges

RSA Laboratories has issued cryptographic challenges. They post ciphertext strings under a specified algorithm, and they offer a cash prize to the first person who correctly finds the corresponding plaintext and decryption key. (For more details, see www.rsasecurity.com/rsalabs/node.asp?id=2091.)

The first challenge, for DES, has already been solved. In a breathtaking 22 hours and 15 minutes, the Electronic Frontier Foundation (EFF) managed to decrypt the DES-encrypted string posted 18 January 1999. The solvers used a network of 100,000 computers to derive the 56-bit key in conjunction with a special-purpose hardware-cracking unit built for approximately $250,000. EFF won an earlier competition with the hardware cracker alone, by finding a key in three days' time [EFF98].

RSA Labs posted challenges for various sizes of RC5 in 1997. The first challenge, RC5-32/12/5, was broken in 3.5 hours. (The notation RC5-x/y/z means RC5 with an x-bit word (block) size, using y rounds and a z-byte key.) RC5-32/12/6 was broken in 313 hours, RC5-32/12/7 in 265 days, and RC5-32/12/8 in 2002 after 1,757 days. Work is underway on RC5-32/12/9 (a 72-bit key). The major contender is the distributed collaboration put together by distributed.net, which won both the /6 and /7 RC-5 challenges.

These challenges are interesting mathematical and cryptological puzzles, but they serve another purpose as well. They show clearly that standard 56-bit DES keys are no longer secure enough to be used for situations requiring any real security. However, 64-bit RC5 keys have required more than four years by a very large network of machines to be broken. This result is encouraging because it indicates that 112-bit triple DES (or the stronger 168-bit variety) is amply secure even for data requiring long-term protection. This analysis matches the 1996 recommendations of a distinguished panel of cryptologists: Blaze et al. [BLA96] said then that for safety, keys in 1996 should be about 75 bits long, and to provide 20 years' of protection 90 bits were preferable. In 2005, NIST investigated encryption algorithms [NIS05] and recommended using 80-bit keys for 5 years of protection, 112-bit keys for 25 years, and 128 bits for more than 25 years.