Data Encryption Standard

Data Encryption Standard

The symmetric systems provide a two-way channel to their users: A and B share a secret key, and they can both encrypt information to send to the other as well as decrypt information from the other. The symmetry of this situation is a major advantage.

As long as the key remains secret, the system also provides authentication, proof that a message received was not fabricated by someone other than the declared sender. Authenticity is ensured because only the legitimate sender can produce a message that will decrypt properly with the shared key.

As we noted in Chapter 2, the Data Encryption Standard (DES) [NBS77] is a system developed for the U.S. government for use by the general public. It has been officially accepted as a cryptographic standard both in the United States and abroad. Many hardware and software systems use the DES. However, its adequacy has recently been questioned.

Overview of the DES Algorithm

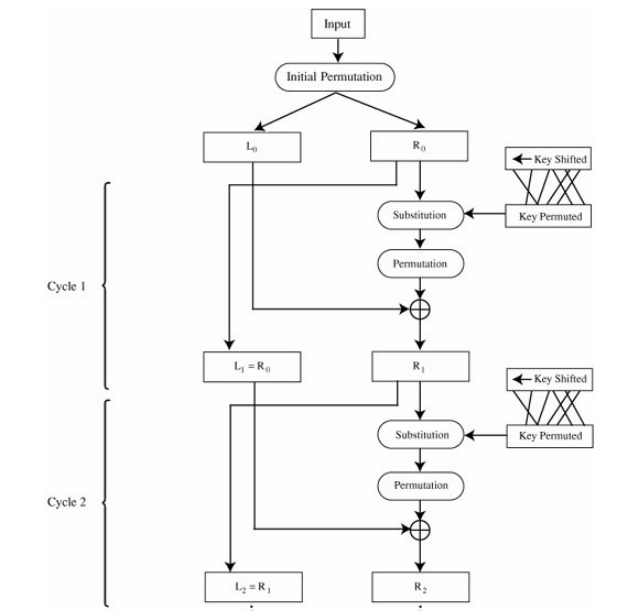
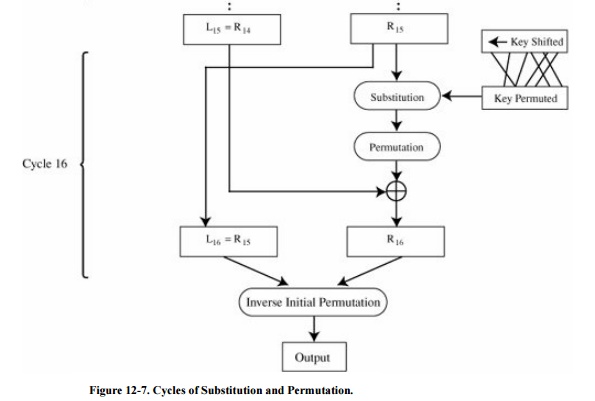
Recall that the strength of the DES algorithm derives from repeated application of substitution and permutation, one on top of the other, for a total of 16 cycles. That is, plaintext is affected by a series of cycles of a substitution then a permutation. The iterative substitutions and permutations are performed as outlined in Figure 12-7.

We noted in Chapter 2 that the algorithm uses only standard arithmetic and logical operations on up to 64-bit numbers, so it is suitable for implementation in software on most current computers. Although complex, the algorithm is repetitive, making it suitable for implementation on a single-purpose chip. In fact, several such chips are available on the market for use as basic components in devices that use DES encryption in an application.

Details of the Encryption Algorithm

The basis of the DES is two different ciphers, applied alternately. Shannon noted that two weak but complementary ciphers can be made more secure by being applied together (called the "product" of the two ciphers) alternately, in a structure called a product cipher. The product of two ciphers is depicted in Figure 12-8.

After initialization, the DES algorithm operates on blocks of data. It splits a data block in half, scrambles each half independently, combines the key with one half, and swaps the two halves. This process is repeated 16 times. It is an iterative algorithm using just table lookups and simple bit operations. Although the bit-level manipulations of the algorithm are complex, the algorithm itself can be implemented quite efficiently. The rest of this section identifies the individual steps of the algorithm. In the next section, we describe each step in full detail.

Input to the DES is divided into blocks of 64 bits. The 64 data bits are permuted by a so-called initial permutation. The data bits are transformed by a 64-bit key (of which only 56 bits are used). The key is reduced from 64 bits to 56 bits by dropping bits 8, 16, 24, … 64 (where the most significant bit is named bit "1"). These bits are assumed to be parity bits that carry no information in the key.

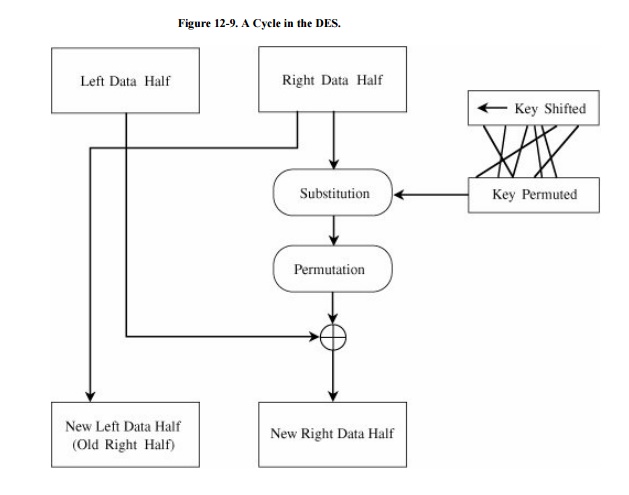
Next begins the sequence of operations known as a cycle. The 64 permuted data bits are broken into a left half and a right half of 32 bits each. The key is shifted left by a number of bits and permuted. The key is combined with the right half, which is then combined with the left half. The result of these combinations becomes the new right half; the old right half becomes the new left half. This sequence of activities, which constitutes a cycle, is shown in Figure 12-9. The cycles are repeated 16 times. After the last cycle is a final permutation, which is the inverse of the initial permutation.

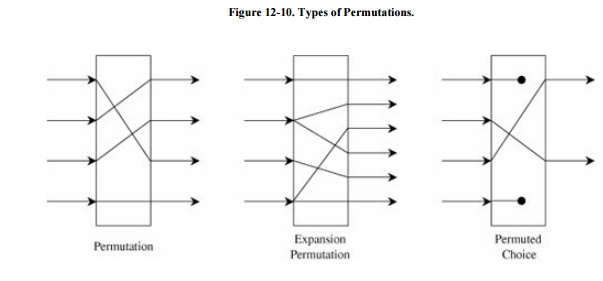
For a 32-bit right half to be combined with a 64 -bit key, two changes are needed. First, the algorithm expands the 32-bit half to 48 bits by repeating certain bits, while reducing the 56-bit key to 48 bits by choosing only certain bits. These last two operations, called expansion permutations and permuted choices, are shown in the diagram of Figure 12-10.

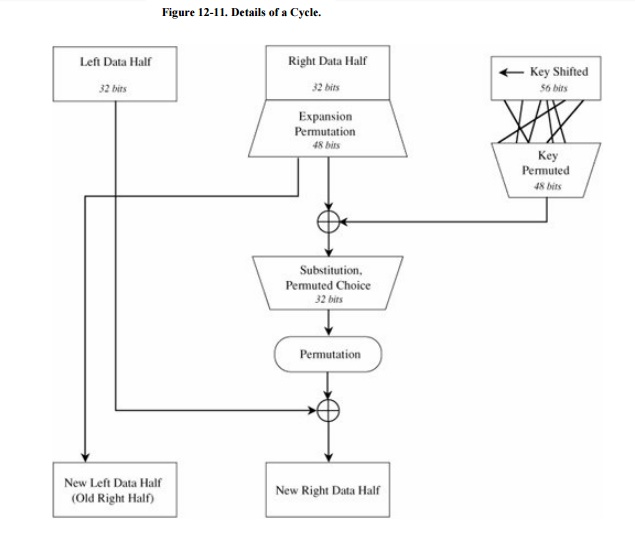
Details of Each Cycle of the Algorithm

Each cycle of the algorithm is really four separate operations. First, a right half is expanded from 32 bits to 48. Then, it is combined with a form of the key. The result of this operation is then substituted for another result and condensed to 32 bits at the same time. The 32 bits are permuted and then combined with the left half to yield a new right half. This whole process is shown in Figure 12-11.

Expansion Permutation

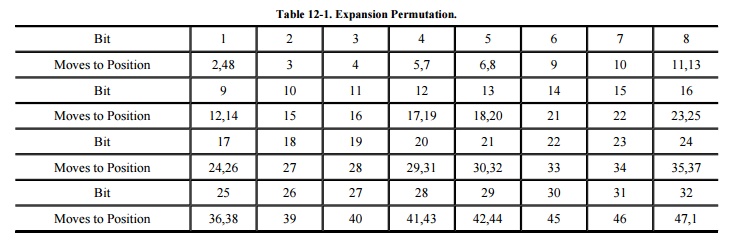
Each right half is expanded from 32 to 48 bits by means of the expansion permutation. The expansion permutes the order of the bits and also repeats certain bits. The expansion has two purposes: to make the intermediate halves of the ciphertext comparable in size to the key and to provide a longer result that can later be compressed.

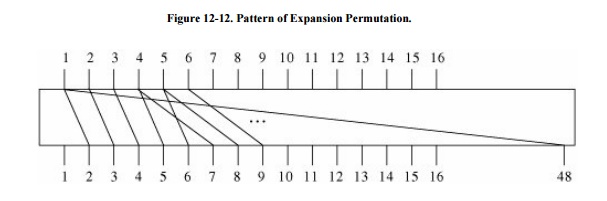
The expansion permutation is defined by Table 12-1. For each 4-bit block, the first and fourth bits are duplicated, while the second and third are used only once. This table shows to which output position(s) the input bits move. Since this is an expansion permutation, some bits move to more than one position. Each row of the table shows the movement of eight bits. The interpretation of this table is that bit 1 moves to positions 2 and 48 of the output, while bit 10 moves to position 15. A portion of the pattern is also shown in Figure 12-12.

Key Transformation

As described above, the 64-bit key immediately becomes a 56-bit key by deletion of every eighth bit. At each step in the cycle, the key is split into two 28 -bit halves, the halves are shifted left by a specified number of digits, the halves are then pasted together again, and 48 of these 56 bits are permuted to use as a key during this cycle.

Next, the key for the cycle is combined by an exclusive OR function with the expanded right half. That result moves into the S-boxes we are about to describe.

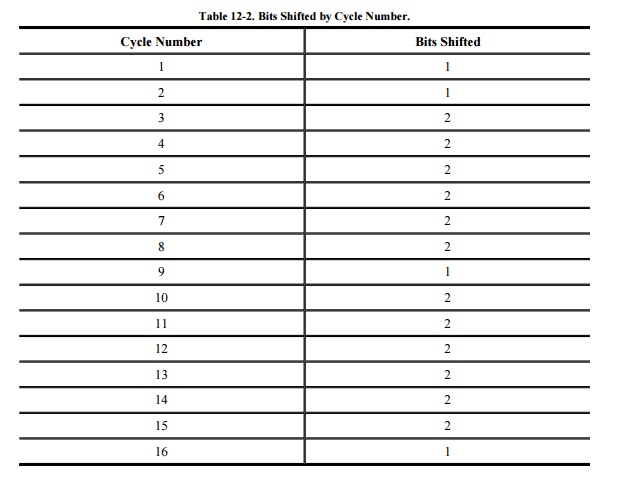
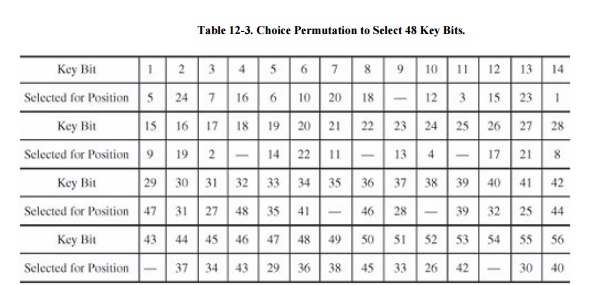
At each cycle, the halves of the key are independently shifted left circularly by a specified number of bit positions. The number of bits shifted is given in Table 12-2.

After being shifted, 48 of the 56 bits are extracted for the exclusive OR combination with the expanded right half. The choice permutation that selects these 48 bits is shown in Table 12-3. For example, from this table we see that bit 1 of the shifted key goes to output position 5, and bit 9 is ignored in this cycle.

S-Boxes

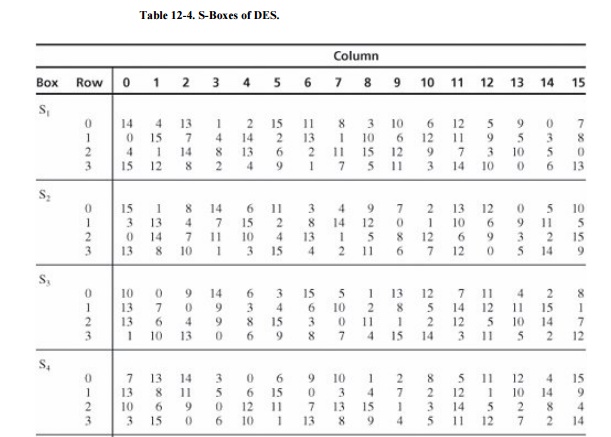
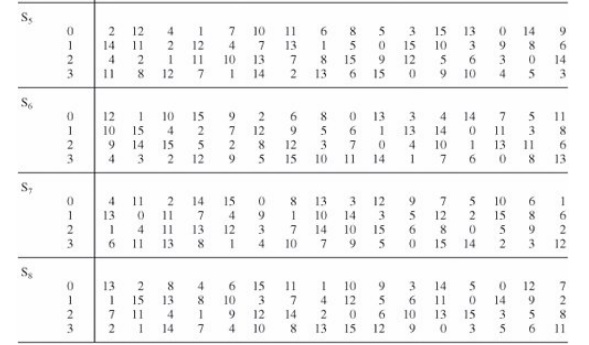
Substitutions are performed by eight S-boxes. An S-box is a permuted choice function by which six bits of data are replaced by four bits. The 48-bit input is divided into eight 6-bit blocks, identified as B₁B₂... B₈; block B_j is operated on by S-box S_j.

The S-boxes are substitutions based on a table of 4 rows and 16 columns. Suppose that block B_j is the six bits b₁b₂b₃b₄b₅b₆. Bits b₁ and b₆, taken together, form a two-bit binary number b₁b₆, having a decimal value from 0 to 3. Call this value r. Bits b₂, b₃, b₄, and b₅ taken together form a 4-bit binary number b₂b₃b₄b₅, having a decimal value from 0 to 15. Call this value c. The substitutions from the S-boxes transform each 6-bit block B_j into the 4-bit result shown in row r, column c of section S_i of Table 12-4. For example, assume that block B₇ in binary is 010011. Then, r = 01 = 1 and c = 1001 = 9. The transformation of block B₇ is found in row 1, column 9 of section 7 of Table 12-4. The value 3 = 0011 is substituted for the value 010011.

P-Boxes

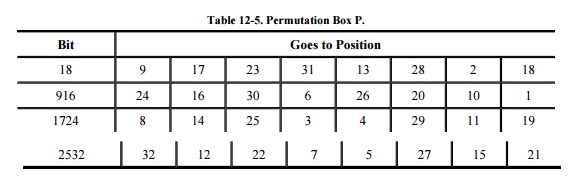
After an S-box substitution, all 32 bits of a result are permuted by a straight permutation, P. Table 12-5 shows the position to which bits are moved. Eight bits are shown on each row. For example, bit 1 of the output of the substitution moves to bit 9, and bit 10 moves to position 16.

Initial and Final Permutations

The DES algorithm begins with an initial permutation that reorders the 64 bits of each input block. The initial permutation is shown in Table 12-6.

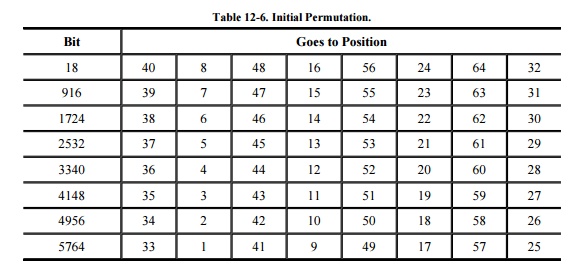
At the conclusion of the 16 substitutionpermutation rounds, the DES algorithm finishes with a final permutation (or inverse initial permutation), which is shown in Table 12-7.

Complete DES

Now we can put all the pieces back together. First, the key is reduced to 56 bits. Then, a block of 64 data bits is permuted by the initial permutation. Following are 16 cycles in which the key is shifted and permuted, half of the data block is transformed with the substitution and permutation functions, and the result is combined with the remaining half of the data block. After the last cycle, the data block is permuted with the final permutation.

Decryption of the DES

The same DES algorithm is used both for encryption and decryption. This result is true because cycle j derives from cycle (j-1) in the following manner:

Equation (1)

Equations (3) and (5) show that these same values could be obtained from the results of later cycles. This property makes the DES a reversible procedure; we can encrypt a string and also decrypt the result to derive the plaintext again.

With the DES, the same function f is used forward to encrypt or backward to decrypt. The only change is that the keys must be taken in reverse order (k₁₆, k₁₅, ..., k₁) for decryption. Using one algorithm either to encrypt or to decrypt is very convenient for a hardware or

software implementation of the DES.

Questions About the Security of the DES

Since its first announcement, there has been controversy concerning the security provided by the DES. Although much of this controversy has appeared in the open literature, certain features of the DES have neither been revealed by the designers nor inferred by outside analysts.

Design of the Algorithm

Initially, there was concern with the basic algorithm itself. During development of the algorithm, the National Security Agency (NSA) indicated that key elements of the algorithm design were "sensitive" and would not be made public. These elements include the rationale behind transformations by the S-boxes, the P-boxes, and the key changes. There are many possibilities for the S-box substitutions, but one particular set was chosen for the DES.

Two issues arose about the design's secrecy. The first involved a fear that certain "trapdoors" had been embedded in the DES algorithm so that a covert, easy means was available to decrypt any DES-encrypted message. For instance, such trapdoors would give NSA the ability to inspect private communications.

After a Congressional inquiry, the results of which are classified, an unclassified summary exonerated NSA from any improper involvement in the DES design. (For a good discussion on the design of DES, see [SMI88a].)

The second issue addressed the possibility that a design flaw would be (or perhaps has been) discovered by a cryptanalyst, this time giving an interceptor the ability to access private communications.

Both Bell Laboratories [MOR77] and the Lexan Corporation [LEX76] scrutinized the operation (not the design) of the S -boxes. Neither analysis revealed any weakness that impairs the proper functioning of the S-boxes. The DES algorithm has been studied extensively and, to date, no serious flaws have been published.

In response to criticism, the NSA released certain information on the selection of the S-boxes ([KON81, BRA77]).

No S-box is a linear or affine function of its input; that is, the four output bits cannot be expressed as a system of linear equations of the six input bits.

Changing one bit in the input of an S-box results in changing at least two output bits; that is, the S-boxes diffuse their information well throughout their outputs.

The S-boxes were chosen to minimize the difference between the number of 1s and 0s when any single input bit is held constant; that is, holding a single bit constant as a 0 or 1 and changing the bits around it should not lead to disproportionately many 0s or 1s in the output.

Number of lterations

Many analysts wonder whether 16 iterations are sufficient. Since each iteration diffuses the information of the plaintext throughout the ciphertext, it is not clear that 16 cycles diffuse the information sufficiently. For example, with only one cycle, a single ciphertext bit is affected only by a few bits of plaintext. With more cycles, the diffusion becomes greater, so ideally no one ciphertext bit depends on any subset of plaintext bits.

Experimentation with both the DES and its IBM predecessor Lucifer was performed by the NBS and by IBM as part of the certification process of the DES algorithm. These experiments have shown [KON81] that 8 iterations are sufficient to eliminate any observed dependence. Thus, the 16 iterations of the DES should surely be adequate.

Key Length

The length of the key is the most serious objection raised. The key in the original IBM implementation of Lucifer was 128 bits, whereas the DES key is effectively only 56 bits long. The argument for a longer key centers around the feasibility of an exhaustive search for a key.

Given a piece of plaintext known to be enciphered as a particular piece of ciphertext, the goal for the interceptor is to find the key under which the encipherment was done. This attack assumes that the same key will be used to encipher other (unknown) plaintext. Knowing the key, the interceptor can easily decipher intercepted ciphertext.

The attack strategy is the "brute force" attack: Encipher the known plaintext with an orderly series of keys, repeating with a new key until the enciphered plaintext matches the known ciphertext. There are 2⁵⁶ 56-bit keys. If someone could test one every 100 milliseconds, the

time to test all keys would be 7.2 * 10¹⁵ seconds, or about 228 million years. If the test took only one microsecond, then the total time for the search is (only!) about 2,280 years. Even supposing the test time to be one nanosecond, infeasible on current technology machines, the search time is still in excess of two years, assuming full-time work with no hardware or software failures!

Diffie and Hellman [DIF77] suggest a parallel attack. With a parallel design, multiple processors can be assigned the same problem  simultaneously. If one chip, working at a rate of one key per microsecond, can check about 8.6 * 1010 keys in one day, it would take 106  days to try all 2⁵⁶ 7 * 10¹⁶ keys. However, 106 chips working in parallel at that rate could check all keys in one day.  

Hellman's original estimate of the cost of such a machine was $20 million (at 1977 prices). The price was subsequently revised upward to $50 million. Assuming a "key shop" existed where people would bring their plaintext/ciphertext pairs to obtain keys and assuming that there was enough business to keep this machine busy 24 hours a day for 5 years, the proportionate cost would be only about $20,000 per solution. As hardware costs continue to fall, the cost of such a machine becomes lower. The stumbling block in the economics of this argument is prorating the cost over five years: If people learned such a device was available at affordable prices, use of the DES would cease for important data. Hellman predicted [HEL79] that hardware prices would fall to the point where this attack would be feasible.

There has been a dramatic drop in the price of computing hardware per instruction per microsecond. In 1998 a piece of special-purpose hardware was built that could infer a DES key in 112 hours for only $130,000. Kocher [KOC99] describes the machine. As the price of hardware continues to drop, the security of DES continues to fall.

An alternative attack strategy is the table lookup argument [HEL80]. For this attack, assume a chosen plaintext attack. That is, assume we have the ability to insert a given plaintext block into the encryption stream and obtain the resulting ciphertext under a still-secret key.

Hellman argues that with enough advance time and enough storage space, it would be possible to compute all of the 2⁵⁶ results of encrypting the chosen block under every possible key. Then, determining which key was used is a matter of looking up the output obtained.

By a heuristic algorithm, Hellman suggests an approach that will limit the amount of computation and data stored to 2³⁷, or about 6.4 * 10¹¹. Again assuming many DES devices working in parallel, it would be possible to precompute and store results.

A brute force parallel attack against DES succeeded in 1997. (Thus, the concerns about key length in 1977 were validated in two decades.) Using the Internet, a team of researchers divided the key search problem into pieces (so that computer A tries all keys beginning 0000..., computer B tries all keys beginning 0001..., computer C tries all keys beginning 0010..., and so forth) . This attack works because the key space is linear: any 56-bit string could be used as a key, and the parallel attack simply divides the key space among all search machines. In four months, using approximately 3500 machines, the researchers were able to recover a key to a DES challenge posted by RSA Laboratories [KOC99]. This challenge required thousands of cooperating participants. It is doubtful that such an attack could be accomplished in secret with public machines. Because the approach is linear, 3500 machines in 120 days is equivalent to 35,000 machines in 12 days.

Weaknesses of the DES

The DES algorithm also has known weaknesses, but these weaknesses are not believed to be serious limitations of the algorithm's effectiveness.

Complements

The first known weakness concerns complements. (Throughout this discussion, "complement" means "ones complement," the result obtained by replacing all 1s by 0s and 0s by 1s in a binary number.) If a message is encrypted with a particular key, the complement of that encryption will be the encryption of the complement message under the complement key. Stated formally, let p represent a plaintext message and k a key, and let the symbol ¬x mean the complement of the binary string x. If c = DES(p, k) (meaning c is the DES encryption of p using key k), then ¬c = DES(¬p, ¬k). Since most applications of encryption do not deal with complement messages and since users can be warned not to use complement keys, this problem is not serious.

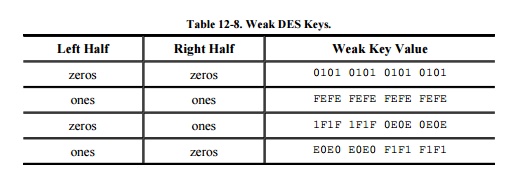
Weak Keys

A second known weakness concerns choice of keys. Because the initial key is split into two halves and the two halves are independently shifted circularly, if the value being shifted is all 0s or all 1s, then the key used for encryption in each cycle is the same as for all other cycles. Remember that the difference between encryption and decryption is that the key shifts are applied in reverse. Key shifts are right shifts, and the number of positions shifted is taken from the bottom of the table up, instead of top down. But if the keys are all 0s or all 1s anyway, right or left shifts by 0, 1, or 2 positions are all the same. For these keys, encryption is the same as decryption: c = DES(p, k), and p = DES(c, k). These keys are called "weak keys." The same thing happens if one half of the key is all 0s and the other half is all 1s. Since these keys are known, they can simply be avoided, so this, too, is not a serious problem.

The four weak keys are shown in hexadecimal notation in Table 12-8. (The initial key permutation extracts every eighth bit as a parity bit and scrambles the key order slightly. Therefore, the "half zeros, half ones" keys are not just split in the middle.)

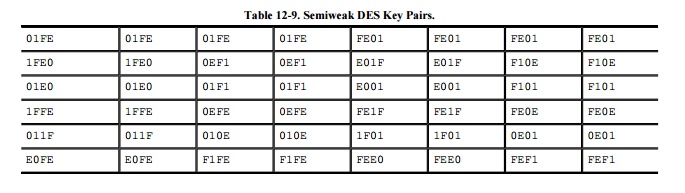
Semiweak Keys

A third difficulty is similar: Specific pairs of keys have identical decryption. That is, there are two different keys, k₁ and k₂, for which c = DES(p, k₁) and c = DES(p, k₂). This similarity implies that k₁ can decrypt a message encrypted under k₂. These socalled semiweak keys are shown in Table 12-9. Other key patterns have been investigated with no additional weaknesses found to date. We should, however, avoid any key having an obvious pattern such as these.

Design Weaknesses

In another analysis of the DES, [DAV83b] shows that the expansion permutation repeats the first and fourth bits of every 4-bit series, crossing bits from neighboring 4-bit series. This analysis further indicates that in S-box S4, one can derive the last three output bits the same way as the first by complementing some of the input bits. Of course, this small weakness raises the question of whether there are similar weaknesses in other S-boxes or in pairs of S-boxes.

It has also been shown that two different, but carefully chosen, inputs to S-boxes can produce the same output (see [DAV83b]). Desmedt et al. [DES84] make the point that in a single cycle, by changing bits only in three neighboring S-boxes, it is possible to obtain the same output; that is, two slightly different inputs, encrypted under the same key, will produce identical results at the end of just one of the l6 cycles.

Key Clustering

Finally, the researchers in [DES84] investigate a phenomenon called "key clustering." They seek to determine whether two different keys can generate the same ciphertext from the same plaintext, that is, two keys can produce the same encryption. The semiweak keys are key clusters, but the researchers seek others. Their analysis is very involved, looking at ciphertexts that produce identical plaintext with different keys in one cycle of the DES, then looking at two cycles, then three, and so forth. Up through three cycles, they found key clusters. Because of the complexity involved, they had to stop the analysis after three cycles.

Differential Cryptanalysis

These inherent design problemsweak keys, key clustering, and so forthwere all discovered through intensive research into the strength of DES shortly after its introduction. Although the results are significant from the standpoint of cryptologists, none of them called into question the overall usefulness of DES.

In 1990 Biham and Shamir [BIH90] (see also [BIH91, BIH92, and BIH93]) announced a technique they named differential cryptanalysis. The technique applied to cryptographic algorithms that use substitution and permutation. This powerful technique was the first to have impressive effects against a broad range of algorithms of this type.

The technique uses carefully selected pairs of plaintext with subtle differences and studies the effects of these differences on resulting ciphertexts. If particular combinations of input bits are modified simultaneously, particular intermediate bits are also likely with a high probability to change in a particular way. The technique looks at the exclusive OR (XOR) of a pair of inputs; the XOR will have a 0 in any bit in which the inputs are identical and a 1 where they differ.

The full analysis is rather complicated, but we present a sketch of it here. The S-boxes transform six bits into four. If the S-boxes were perfectly uniform, one would expect all 4-bit outputs to be equally likely. However, as Biham and Shamir show, certain similar texts are more likely to produce similar outputs than others. For example, examining all pairs of 6-bit strings with an XOR pattern 35 in hexadecimal notation (that is, strings of the form ddsdsd where d means the bit value is different between the two strings and s means the bit value is the same) for S-box S₁, the researchers found that the pairs have an output pattern of dsss 14 times, ddds 14 times, and all other patterns a

frequency ranging between 0 and 8. That says that an input of the form ddsdsd has an output of the form dsss 14 times out of 64, and ddds another 14 times out of 64; each of these results is almost 1/4, which continues to the next round. Biham and Shamir call each of these recognizable effects a "characteristic"; they then extend their result by concatenating characteristics. The attack lets them infer values in

specific positions of the key. If m bits of a k-bit key can be found, the remaining (k-m) bits can be found in an exhaustive search of all 2^(k-m) possible keys; if m is large enough, the 2^(k-m) exhaustive search is feasible.

In Biham and Shamir [BIH90] the authors present the conclusions of many results they have produced by using differential cryptanalysis;  they describe the details of these results in the succeeding papers. The attack on Lucifer, the IBM-designed predecessor to DES, succeeds with only 30 ciphertext pairs. FEAL is an algorithm similar to DES that uses any number of rounds; the n-round version is called FEAL-n.  

FEAL-4 can be broken with 20 chosen plaintext items [MUR90], FEAL-8 [MIY89] with 10,000 pairs [GIL90]; and FEAL-n for n 31  can be broken faster by differential cryptanalysis than by full exhaustive search [BIH91].

The results concerning DES are impressive. Shortening DES to fewer than its normal 16 rounds allows a key to be determined from chosen ciphertexts in fewer than the 2⁵⁶ (actually, expected value of 2⁵⁵) searches. For example, with 15 rounds, only 2⁵² tests are needed (which is still a large number of tests); with 10 rounds, the number of tests falls to 2³⁵, and with 6 rounds, only 2⁸ tests are needed. However, with the full 16 rounds, this technique requires 2⁵⁸ tests, or 2² = 4 times more than an exhaustive search would require.

Finally, the authors show that with randomly selected S-box values, DES is easy to break. Indeed, even with a change of only one entry in one S-box, DES becomes easy to break. One might conclude that the design of the S-boxes and the number of rounds were chosen to be optimal.

In fact, that is true. Don Coppersmith of IBM, one of the original team working on Lucifer and DES, acknowledged [COP92] that the technique of differential cryptanalysis was known to the design team in 1974 when they were designing DES. The S-boxes and permutations were chosen in such a way as to defeat that line of attack.

Security of the DES

The cryptanalytic attacks described here have not exposed any significant, exploitable vulnerabilities in the design of DES. But the weakness of the 56-bit key is now apparent. Although the amount of computing power or time needed is still significant enough to deter casual DES key browsing, a dedicated adversary could succeed against a specific DES ciphertext of significant interest.

Does this mean the DES is insecure? No, not yet. Nobody has yet shown serious flaws in the DES. With a triple DES approach (described

in Chapter 2), the effective key length is raised from 56 bits to 112 or 168 bits,^[4] increasing the difficulty of attack exponentially. In the near term (years, probably decades) triple DES is strong enough to protect even significant commercial data (such as financial data or patient medical records). Still, DES is nearing the end of its useful lifetime, and a replacement is in order. With millions of computers in the world, clearly DES is inadequate to protect sensitive information with a modest time value. Similarly, algorithms with key lengths of 64 and 80 bits may be strong enough for a while, but an improvement in processor speeds and number of parallel computers threatens those, too. (See [BLA96] and [LEN01] for more discussion on the relationship between key length and security with various algorithms.)