Measuring and Improving Cache Performance

MEASURING AND IMPROVING CACHE PERFORMANCE

As a working example, suppose the cache has 2⁷ = 128 lines, each with 2⁴ = 16 words. Suppose the memory has a 16-bit address, so that 2¹⁶ = 64K words are in the memory's address space.

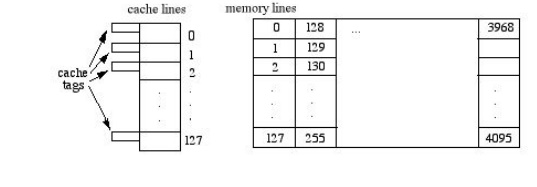
Direct Mapping

Under this mapping scheme, each memory line j maps to cache line j mod 128 so the memory address looks like this:

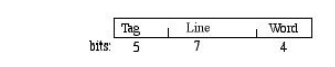
Here, the "Word" field selects one from among the 16 addressable words in a line. The "Line" field defines the cache line where this memory line should reside. The "Tag" field of the address is is then compared with that cache line's 5-bit tag to determine whether there is a hit or a miss. If there's a miss, we need to swap out the memory line that occupies that position in the cache and replace it with the desired memory line.

E.g., Suppose we want to read or write a word at the address 357A, whose 16 bits are 0011010101111010. This translates to Tag = 6, line = 87, and Word = 10 (all in decimal). If line 87 in the cache has the same tag (6), then memory address 357A is in the cache. Otherwise, a miss has occurred and the contents of cache line 87 must be replaced by the memory line 001101010111 = 855 before the read or write is executed.

Direct mapping is the most efficient cache mapping scheme, but it is also the least effective in its utilization of the cache - that is, it may leave some cache lines unused.

Associative Mapping

This mapping scheme attempts to improve cache utilization, but at the expense of speed. Here, the cache line tags are 12 bits, rather than 5, and any memory line can be stored in any cache line. The memory address looks like this:

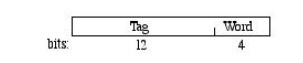
Here, the "Tag" field identifies one of the 2 ¹² = 4096 memory lines; all the cache tags are searched to find out whether or not the Tag field matches one of the cache tags. If so, we have a hit, and if not there's a miss and we need to replace one of the cache lines by this line before reading or writing into the cache. (The "Word" field again selects one from among 16 addressable words (bytes) within the line.)

For example, suppose again that we want to read or write a word at the address 357A, whose 16 bits are 0011010101111010. Under associative mapping, this translates to Tag = 855 and Word = 10 (in decimal). So we search all of the 128 cache tags to see if any one of them will match with 855. If not, there's a miss and we need to replace one of the cache lines with line 855 from memory before completing the read or write.

The search of all 128 tags in the cache is time-consuming. However, the cache is fully utilized since none of its lines will be unused prior to a miss (recall that direct mapping may detect a miss even though the cache is not completely full of active lines).

Set-associative Mapping

This scheme is a compromise between the direct and associative schemes described above. Here, the cache is divided into sets of tags, and the set number is directly mapped from the memory address (e.g., memory line j is mapped to cache set j mod 64), as suggested by the diagram below:

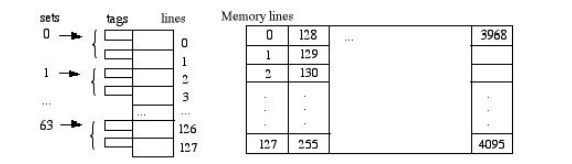
The memory address is now partitioned to like this:

Here, the "Tag" field identifies one of the 2⁶ = 64 different memory lines in each of the 2⁶ = 64 different "Set" values. Since each cache set has room for only two lines at a time, the search for a match is limited to those two lines (rather than the entire cache). If there's a match, we have a hit and the read or write can proceed immediately.

Otherwise, there's a miss and we need to replace one of the two cache lines by this line before reading or writing into the cache. (The "Word" field again select one from among 16 addressable words inside the line.) In set-associative mapping, when the number of lines per set is n, the mapping is called n-way associative. For instance, the above example is 2-way associative.

E.g., Again suppose we want to read or write a word at the memory address 357A, whose 16 bits are 0011010101111010. Under set-associative mapping, this translates to Tag = 13, Set = 23, and Word = 10 (all in decimal). So we search only the two tags in cache set 23 to see if either one matches tag 13. If so, we have a hit. Otherwise, one of these two must be replaced by the memory line being addressed (good old line 855) before the read or write can be executed.

A Detailed Example

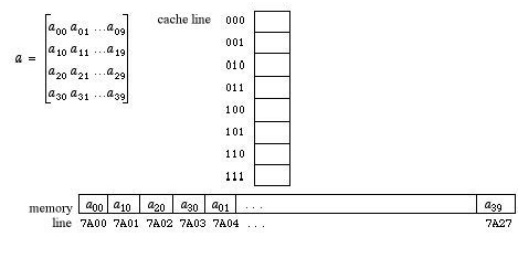
Suppose we have an 8-word cache and a 16-bit memory address space, where each memory "line" is a single word (so the memory address need not have a "Word" field to distinguish individual words within a line). Suppose we also have a 4x10 array a of numbers (one number per addressible memory word) allocated in memory column-by-column, beginning at address 7A00. That is, we have the following declaration and memory allocation picture for

The array a:

float [a = new float [4][10];

Here  is  a  simple  equation  that  recalculates  the  elements  of  the  first  row  of  a:

This  calculation could  have  been  implemented directly  in  C/C++/Java  as  follows:

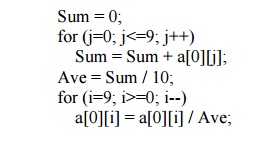
The emphasis here is on the underlined parts of this program which represent memory read and write operations in the array a. Note that the 3rd and 6th lines involve a memory read of a[0][j] and a[0][i], and the 6th line involves a memory write of a[0][i]. So altogether, there are 20 memory reads and 10 memory writes during the execution of this program. The following discussion focusses on those particular parts of this program and their impact on the cache.

Direct Mapping

Direct mapping of the cache for this model can be accomplished by using the rightmost 3 bits of the memory address. For instance, the memory address 7A00 = 0111101000000 000, which maps to cache address 000. Thus, the cache address of any value in the array a is just its memory address modulo 8.

Using this scheme, we see that the above calculation uses only cache words 000 and 100, since each entry in the first row of a has a memory address with either 000 or 100 as its rightmost 3 bits. The hit rate of a program is the number of cache hits among its reads and writes divided by the total number of memory reads and writes. There are 30 memory reads and writes for this program, and the following diagram illustrates cache utilization for direct mapping throughout the life of these two loops:

Reading the sequence of events from left to right over the ranges of the indexes i and j, it is easy to pick out the hits and misses. In fact, the first loop has a series of 10 misses (no hits). The second loop contains a read and a write of the same memory location on each repetition (i.e., a[0][i] = a[0][i]/Ave; ), so that the 10 writes are guaranteed to be hits. Moreover, the first two repetitions of the second loop have hits in their read operations, since a₀₉ and a₀₈ are still in the cache at the end of the first loop. Thus, the hit rate for direct mapping in this algorithm is 12/30 = 40%

Associative Mapping

Associative mapping for this problem simply uses the entire address as the cache tag. If we use the least recently used cache replacement strategy, the sequence of events in the cache after the first loop completes is shown in the left-half of the following diagram. The second loop happily finds all of a ₀₉ - a₀₂ already in the cache, so it will experience a series of 16 hits (2 for each repetition) before missing on a ₀₁ when i=1. The last two steps of the second loop therefore have 2 hits and 2 misses.

Set-Associative Mapping

Set associative mapping tries to compromise these two. Suppose we divide the cache into two sets, distinguished from each other by the rightmost bit of the memory address, and assume the least recently used strategy for cache line replacement. Cache utilization for our program can now be pictured as follows:

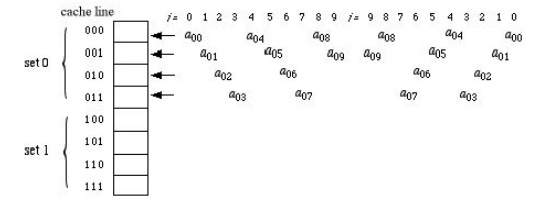
Here all the entries in a that are referenced in this algorithm have even-numbered addresses (their rightmost bit = 0), so only the top half of the cache is utilized. The hit rate is therefore slightly worse than associative mapping and slightly better than direct. That is, set-associative cache mapping for this program yields 14 hits out of 30 read/writes for a hit rate of 46%.