Math - java.lang

Math

The Math class contains all the floating-point functions that are used for geometry and trigonometry, as well as several general-purpose methods. Math defines two double constants: E (approximately 2.72) and PI (approximately 3.14).

Trigonometric Functions

The following methods accept a double parameter for an angle in radians and return the result of their respective trigonometric function:

Method : Description

static double sin(double arg) : Returns the sine of the angle specified by arg in radians.

static double cos(double arg) : Returns the cosine of the angle specified by arg in radians.

static double tan(double arg) : Returns the tangent of the angle specified by arg in radians.

The next methods take as a parameter the result of a trigonometric function and return, in radians, the angle that would produce that result. They are the inverse of their non-arc companions.

Method : Description

static double asin(double arg) : Returns the angle whose sine is specified by arg.

static double acos(double arg) : Returns the angle whose cosine is specified by arg.

static double atan(double arg) : Returns the angle whose tangent is specified by arg.

static double atan2(double x, double y) : Returns the angle whose tangent is x/y.

The next methods compute the hyperbolic sine, cosine, and tangent of an angle:

Method : Description

static double sinh(double arg) : Returns the hyperbolic sine of the angle specified by arg.

static double cosh(double arg) : Returns the hyperbolic cosine of the angle specified by arg.

static double tanh(double arg) : Returns the hyperbolic tangent of the angle specified by arg.

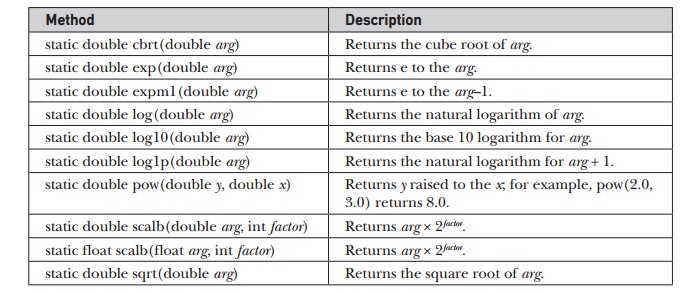
Exponential Functions

Math defines the following exponential methods:

Rounding Functions

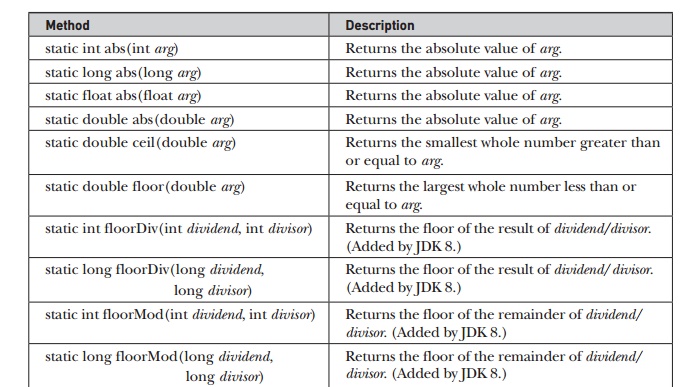
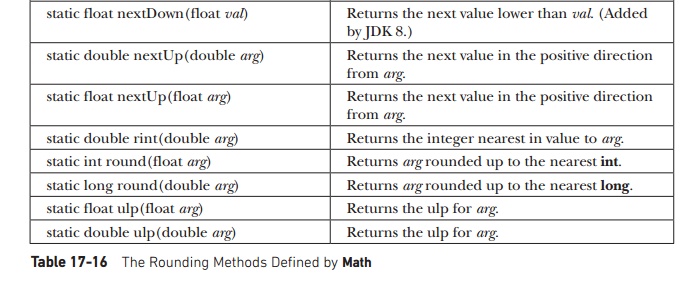
The Math class defines several methods that provide various types of rounding operations. They are shown in Table 17-16. Notice the two ulp( ) methods at the end of the table. In this context, ulp stands for units in the last place. It indicates the distance between a value and the next higher value. It can be used to help assess the accuracy of a result.

Miscellaneous Math Methods

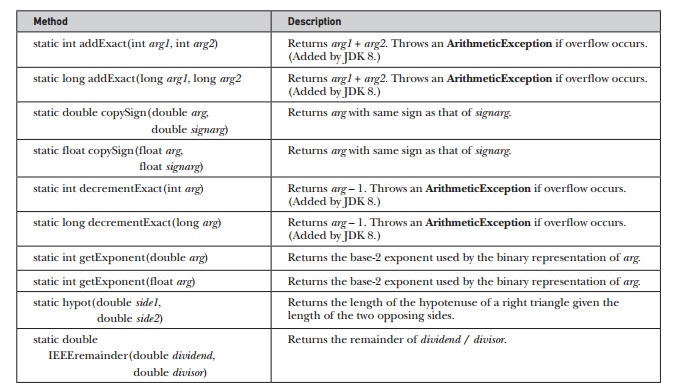
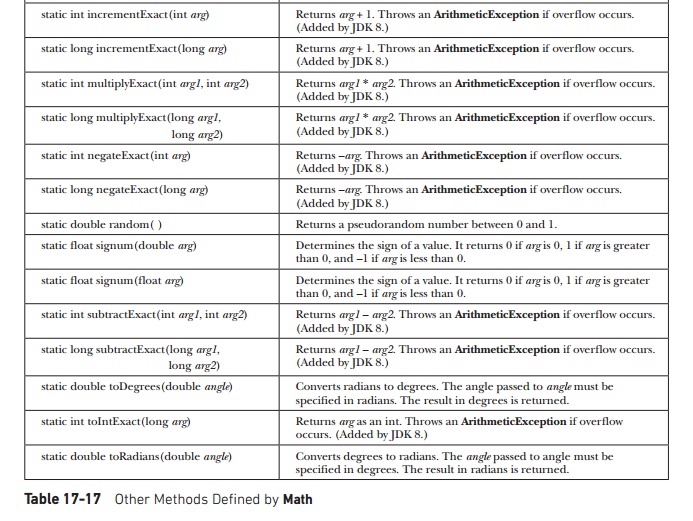
In addition to the methods just shown, Math defines several other methods, which are shown in Table 17-17. Notice that several of the methods use the suffix Exact. These were added by JDK 8. They throw an ArithmeticException if overflow occurs. Thus, these methods give you an easy way to watch various operations for overflow.

The following program demonstrates toRadians( ) and toDegrees( ):

// Demonstrate toDegrees() and toRadians().

class Angles {

public static void main(String args[]) { double theta = 120.0;