Magnetron

MAGNETRON

MAGNETRON OSCILLATORS

Hull invented the magnetron in 1921 , but it was only an interesting laboratory device until about 1940. During World War II, an urgent need for high-power microwave generators for radar transmitters led to the rapid development of the magnetron to its present state.

All magnetrons consist of some form of anode and cathode operated in a de magnetic field normal to of the crossed field between the cathode and anode, the electrons emitted from the cathode are influenced by the crossed field to move in curved paths. If the de magnetic field is strong enough, the electrons will not arrive in the anode but return instead to the cathode. Consequently, the anode current is cut off. Magnetrons can be classified into three types:

1.Split-anode magnetron: This type of magnetron uses a static negative resistance between two anode segments.

2.Cyclotron-frequency magnetrons: This type operates under the influence of synchronism between an alternating component of electric field and a periodic oscillation of electrons in a direction parallel to the field.

3.Traveling-wave magnetrons: This type depends on the interaction of electrons with a traveling electromagnetic field of linear velocity. They are customarily referred to simply as magnetrons.

Cylindrical Magnetron

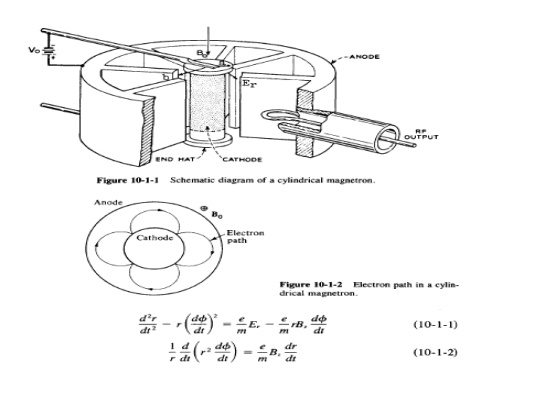
A schematic diagram of a cylindrical magnetron oscillator is shown in Fig. 10-1-1. This type of magnetron is also called a conventional magnetron.

In a cylindrical magnetron, several reentrant cavities are connected to the gaps. The de voltage Vo is applied between the cathode and the anode. The magnetic flux density Bo is in the positive z direction. When the de voltage and the magnetic flux are adjusted properly, the electrons will follow cycloidal paths in the cathodeanode space under the combined force of both electric and magnetic fields as shown inFig. 10-1-2.

Equations of electron motion. The equations of motion for electrons in a cylindrical magnetron can be written with the aid of Eqs.(l-2-Sa) and (1-2-Sb) as

Cyclotron angular frequency. Since the magnetic field is normal to the motion of electrons that travel in a cycloidal path, the outward centrifugal force is equal to the pulling force. Hence

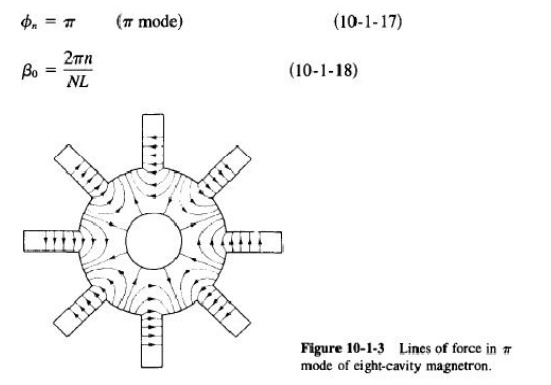
Since the slow-wave structure is closed on itself, or "reentrant," oscillations are possible only if the total phase shift around the structure is an integral multiple of 27T radians. Thus, if there are N reentrant cavities in the anode structure, the phase shift between two adjacent cavities can be expressed as

where n is an integer indicating the nth mode of oscillation. In order for oscillations to be produced in the structure, the anode de voltage must be adjusted so that the average rotational velocity of the electrons corresponds to the phase velocity of the field in the slow-wave structure. Magnetron oscillators are ordinarily operated in the 7T mode. That is

Maxwell's equations subject to the boundary conditions. The solution for the fundamental cf> component of the electric field has the form

where £ 1 is a constant and f3o is given in Eq. (10-1-18). Thus, the traveling field of the fundamental mode travels around the structure with angular velocity

where~ can be found from Eq. (10-1-19). When the cyclotron frequency of the electrons is equal to the angular frequency of the field, the interactions between the field and electron occurs and the energy is transferred. That is,