Introduction to Data-Flow Analysis

Introduction to Data-Flow Analysis

1 The Data-Flow Abstraction

2 The Data-Flow Analysis Schema

3 Data-Flow Schemas on Basic Blocks

4 Reaching Definitions

5 Live-Variable Analysis

6 Available Expressions

7 Summary

8 Exercises for Section 9.2

All the optimizations introduced in Section 9.1 depend on data-flow analysis. "Data-flow analysis" refers to a body of techniques that derive information about the flow of data along program execution paths. For example, one way to implement global common subexpression elimination requires us to determine whether two textually identical expressions evaluate to the same value along any possible execution path of the program. As another example, if the result of an assignment is not used along any subsequent execution path, then we can eliminate the assignment as dead code. These and many other important questions can be answered by data-flow analysis.

1. The Data-Flow Abstraction

Following Section 1.6.2, the execution of a program can be viewed as a series of transformations of the program state, which consists of the values of all the variables in the program, including those associated with stack frames below the top of the run-time stack. Each execution of an intermediate-code statement transforms an input state to a new output state. The input state is associated with the program point before the statement and the output state is associated with the program point after the statement.

When we analyze the behavior of a program, we must consider all the pos-sible sequences of program points ("paths") through a flow graph that the pro-gram execution can take. We then extract, from the possible program states at each point, the information we need for the particular data-flow analysis problem we want to solve. In more complex analyses, we must consider paths that jump among the flow graphs for various procedures, as calls and returns are executed. However, to begin our study, we shall concentrate on the paths through a single flow graph for a single procedure.

Let us see what the flow graph tells us about the possible execution paths.

            Within one basic block, the program point after a statement is the same as the program point before the next statement.

            If there is an edge from block B1 to block E>₂ , then the program point after the last statement of By may be followed immediately by the program point before the first statement of B₂.

Thus, we may define an  execution path (or just path) from point pi  to point pn to  be  a sequence  of points pi,p2,...  ,pn such that  for each i  =  1,2, ... ,n - 1, either

            Pi is the point immediately preceding a statement and pi₊i is the point immediately following that same statement, or

pi is the end of some block and p_i+1    is the beginning of a successor block.

In general, there is an infinite number of possible execution paths through a program, and there is no finite upper bound on the length of an execution path. Program analyses summarize all the possible program states that can occur at a point in the program with a finite set of facts. Different analyses may choose to abstract out different information, and in general, no analysis is necessarily a perfect representation of the state.

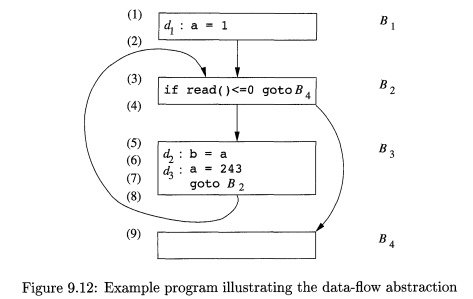
Example 9 . 8 : Even the simple program in Fig. 9.12 describes an unbounded number of execution paths. Not entering the loop at all, the shortest com-plete execution path consists of the program points (1,2,3,4,9) . The next shortest path  executes one  iteration of the loop and consists of the  points ( 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 3 , 4 , 9 ) . We know that, for example, the first time program point  (5) is executed, the value of a is 1  due to definition d1. We say that  d i reaches point (5) i n the f i r s t iteration. I n subsequent iterations, ^ 3 reaches point (5) and the value of a is 243.

In general, it is not possible to keep track of all the program states for all possible paths. In data-flow analysis, we do not distinguish among the paths taken to reach a program point. Moreover, we do not keep track of entire states; rather, we abstract out certain details, keeping only the data we need for the purpose of the analysis. Two examples will illustrate how the same program states may lead to different information abstracted at a point.

1. To help users debug their programs, we may wish to find out what are all the values a variable may have at a program point, and where these values may be defined. For instance, we may summarize all the program states at point (5) by saying that the value of a is one of {1,243}, and that it may be defined by one of { ^ 1 , ^ 3 } . The definitions that may reach a program point along some path are known as reaching definitions.

2. Suppose, instead, we are interested in implementing constant folding. If a use of the variable x is reached by only one definition, and that definition

assigns a constant to x, then we can simply replace x by the constant. If, on the other hand, several definitions of x may reach a single program point, then we cannot perform constant folding on x. Thus, for constant folding we wish to find those definitions that are the unique definition of their variable to reach a given program point, no matter which execution path is taken. For point (5) of Fig. 9.12, there is no definition that must be the definition of a at that point, so this set is empty for a at point (5). Even if a variable has a unique definition at a point, that definition must assign a constant to the variable. Thus, we may simply describe certain variables as "not a constant," instead of collecting all their possible values or all their possible definitions.

Thus, we see that the same information may be summarized differently, de-pending on the purpose of the analysis. •

2. The Data-Flow Analysis Schema

In each application of data-flow analysis, we associate with every program point a data-flow value that represents an abstraction of the set of all possible program states that can be observed for that point.  The set of possible data-flow values is the domain for this application. For example, the domain of data-flow values for reaching definitions is the set of all subsets of definitions in the program.

A particular data-flow value is a set of definitions, and we want to associate with each point in the program the exact set of definitions that can reach that point. As discussed above, the choice of abstraction depends on the goal of the analysis; to be efficient, we only keep track of information that is relevant.

We denote the data-flow values before and after each statement s by IN[S ] and OUT[s], respectively. The  data-flow problem is to find a solution to a set of constraints on the IN[S]'S and OUT[s]'s, for all statements s. There are two sets of constraints: those based on the semantics of the statements ("transfer functions") and those based on the flow of control.

Transfer     Functions

The data-flow values before and after a statement are constrained by the se-mantics of the statement. For example, suppose our data-flow analysis involves determining the constant value of variables at points. If variable a has value v before executing statement b = a, then both a and b will have the value v after the statement.  This relationship between the data-flow values before and after the assignment  statement  is  known  as  a  transfer function.  

 Transfer functions come in two flavors: information may propagate forward along execution paths, or it may flow backwards up the execution paths.  In a forward-flow problem, the transfer function of a statement s, which we shall usually denote f(a), takes the data-flow value before the statement and produces a new data-flow value after the statement.  That is,

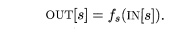
Conversely, in a backward-flow problem, the transfer function f(a) for statement 8 converts a data-flow value after the statement to a new data-flow value before the statement. That is,

Control – Flow Constraints

The second set of constraints on data-flow values is derived from the flow of control. Within a basic block, control flow is simple. If a block B consists of statements s1, s ₂ , • • • ,s_n in that order, then the control-flow value out of Si is the same as the control-flow value into Si+i. That is,

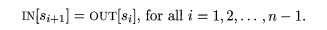
However, control-flow edges between basic blocks create more complex con-

straints between the last statement of one basic block and the first statement

of the following block. For example, if we are interested in collecting all the definitions that may reach a program point, then the set of definitions reaching the leader statement of a basic block is the union of the definitions after the last statements of each of the predecessor blocks. The next section gives the details of how data flows among the blocks.

3.  Data-Flow Schemas on Basic Blocks

While a data-flow schema technically involves data-flow values at each point in the program, we can save time and space by recognizing that what goes on inside a block is usually quite simple. Control flows from the beginning to the end of the block, without interruption or branching. Thus, we can restate the schema in terms of data-flow values entering and leaving the blocks. We denote the data-flow values immediately before and immediately after each basic block B by m[B] and 0 U T [ S ] , respectively. The constraints involving m[B] and 0UT[B] can be derived from those involving w[s] and OUT[s] for the various statements s in B as follows.

Suppose block B consists of statements s 1 , . . .  , sn, in that order.  If si is the first statement of basic block B, then m[B] =  I N [ S I ] , Similarly, if sn    is the last statement of basic block B, then OUT[S] = OUT[s„] . The transfer function of a basic block B, which we denote fB, can be derived by composing the transfer functions of the statements in the block.  That is, let fa.  be the transfer function of statement  st.  Then  of statement si. Then fB = f,sn, o . . . o f,s2, o fsl. . The relationship between the beginning and end of the block is

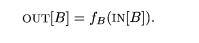
The constraints due to control flow between basic blocks can easily be rewrit-ten by substituting IN[B] and OVT[B] for IN[SI ] and OUT[sn], respectively. For instance, if data-flow values are information about the sets of constants that may be assigned to a variable, then we have a forward-flow problem in which

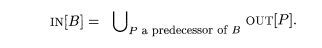
When the data-flow is backwards as we shall soon see in live-variable analy-sis, the equations are similar, but with the roles of the IN's and OUT's reversed. That is,

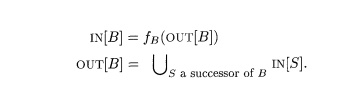
Unlike linear arithmetic equations, the data-flow equations usually do not have a unique solution. Our goal is to find the most "precise" solution that satisfies the two sets of constraints: control-flow and transfer constraints. That is, we need a solution that encourages valid code improvements, but does not justify unsafe transformations — those that change what the program com-putes. This issue is discussed briefly in the box on "Conservatism" and more extensively in Section 9.3.4. In the following subsections, we discuss some of the most important examples of problems that can be solved by data-flow analysis.

4. Reaching Definitions

"Reaching definitions" is one of the most common and useful data-flow schemas. By knowing where in a program each variable x may have been defined when control reaches each point p, we can determine many things about x. For just two examples, a compiler then knows whether x is a constant at point p, and a debugger can tell whether it is possible for x to be an undefined variable, should x be used at p.

We say a definition d reaches a point p if there is a path from the point immediately following d to p, such that d is not "killed" along that path. We kill a definition of a variable x if there is any other definition of x anywhere along the path . ³ Intuitively, if a definition d of some variable x reaches point p, then d might be the place at which the value of x used at p was last defined.

A definition of a variable x is a statement that assigns, or may assign, a value to x. Procedure parameters, array accesses, and indirect references all may have aliases, and it is not easy to tell if a statement is referring to a particular variable x. Program analysis must be conservative; if we do not

³ N o te that the path may have loops, so we could come to another occurrence of d along the path, which does not "kill" d.

Detecting Possible Uses Before Definition

Here is how we use a solution to the reaching-definitions problem to detect uses before definition. The trick is to introduce a dummy definition for each variable x in the entry to the flow graph. If the dummy definition of x reaches a point p where x might be used, then there might be an opportunity to use x before definition. Note that we can never be abso-lutely certain that the program has a bug, since there may be some reason, possibly involving a complex logical argument, why the path along which p is reached without a real definition of x can never be taken.

know whether a statement s is assigning a value to x, we must assume that it may assign to it; that is, variable x after statement s may have either its original value before s or the new value created by s. For the sake of simplicity, the rest of the chapter assumes that we are dealing only with variables that have no aliases. This class of variables includes all local scalar variables in most languages; in the case of C and C++, local variables whose addresses have been computed at some point are excluded.

Example 9 . 9 :  Shown in Fig. 9.13 is a flow graph with seven definitions.  Let us focus on the definitions reaching block B2  •  All the definitions in block B1 reach the beginning of block B2. The definition d§: j = j - 1 in block B2    also reaches the beginning of block B2, because no other definitions of j can be found in the loop leading back to B2.  This definition, however, kills the definition d2: j =  n, preventing it from reaching B% or J34 . The statement d4:  i =  i+1 in B2 does not reach the beginning of B2 though, because the variable i is always redefined by d^: i = u3 . Finally, the definition d 6 : a = u2 also reaches the beginning of block B2.

By defining reaching definitions as we have, we sometimes allow inaccuracies. However, they are all in the "safe," or "conservative," direction. For example, notice our assumption that all edges of a flow graph can be traversed. This assumption may not be true in practice. For example, for no values of a and b can the flow of control actually reach statement 2 in the following program fragment:

if (a ==  b) statement 1; else  if (a == b)  statement 2;

To decide in general whether each path in a flow graph can be taken is an undecidable problem. Thus, we simply assume that every path in the flow graph can be followed in some execution of the program. In most applications of reaching definitions, it is conservative to assume that a definition can reach a point even if it might not. Thus, we may allow paths that are never be traversed in any execution of the program, and we may allow definitions to pass through ambiguous definitions of the same variable safely.

Conservatism in Data-Flow Analysis

Since all data-flow schemas compute approximations to the ground truth (as defined by all possible execution paths of the program), we are obliged to assure that any errors are in the "safe" direction. A policy decision is safe (or conservative) if it never allows us to change what the program computes. Safe policies may, unfortunately, cause us to miss some code improvements that would retain the meaning of the program, but in essen-tially all code optimizations there is no safe policy that misses nothing. It would generally be unacceptable to use an unsafe policy — one that sped up the code at the expense of changing what the program computes.

Thus, when designing a data-flow schema, we must be conscious of how the information will be used, and make sure that any approximations we make are in the "conservative" or "safe" direction. Each schema and application must be considered independently. For instance, if we use reaching definitions for constant folding, it is safe to think a definition reaches when it doesn't (we might think x is not a constant, when in fact it is and could have been folded), but not safe to think a definition doesn't reach when it does (we might replace x by a constant, when the program would at times have a value for x other than that constant).

Transfer  Equations for  Reaching Definitions

We shall now set up the constraints for the reaching definitions problem. We start by examining the details of a single statement. Consider a definition

Here, and frequently in what follows, + is used as a generic binary operator. This statement "generates" a definition d of variable u and "kills" all the

other definitions in the program that define variable u, while leaving the re-maining incoming definitions unaffected. The transfer function of definition d thus can be expressed as

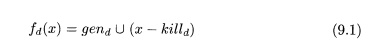
where gend = {d}, the set of definitions generated by the statement, and killd is the set of all other definitions of u in the program.

As discussed in Section 9.2.2, the transfer function of a basic block can be found by composing the transfer functions of the statements contained therein. The composition of functions of the form (9.1), which we shall refer to as "gen-kill form," is also of that form, as we can see as follows. Suppose there are two functions fi(x) = gen1 U (x - kill1) and f2(x) = gen2 U (x — kill2). Then

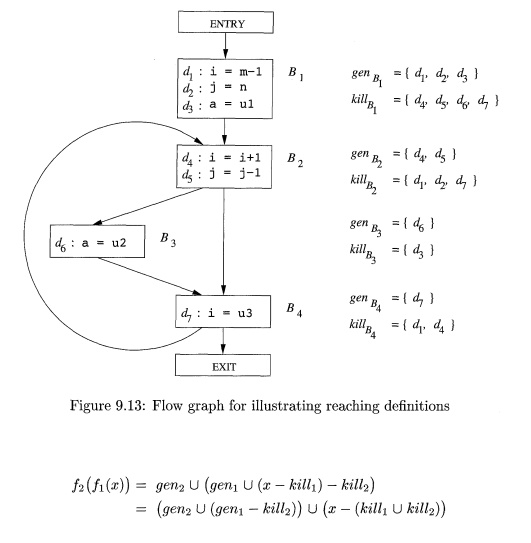
This rule extends to a block consisting of any number of statements. Suppose block B has n statements, with transfer functions fi(x) = geni U (x — kilh) for i = 1,2, ... , n. Then the transfer function for block B may be written as:

Thus, like a statement, a basic block also generates a set of definitions and kills a set of definitions. The gen set contains all the definitions inside the block that are "visible" immediately after the block — we refer to them as downwards exposed. A definition is downwards exposed in a basic block only if it is not "killed" by a subsequent definition to the same variable inside the same basic block. A basic block's kill set is simply the union of all the definitions killed by the individual statements. Notice that a definition may appear in both the gen and kill set of a basic block. If so, the fact that it is in gen takes precedence, because in gen-kill form, the kill set is applied before the gen set.

Example 9 . 1 0 : The gen set for the basic block

is {d2} since d1 is not downwards exposed.  The kill set contains both d1  and d2,  since d1 kills d2    and vice versa.  Nonetheless, since the subtraction of the kill set precedes the union operation with the gen set, the result of the transfer function for this block always includes definition d2.

Control - Flow     Equations

Next, we consider the set of constraints derived from the control flow between basic blocks. Since a definition reaches a program point as long as there exists at least one path along which the definition reaches, O U T [ P ] C m[B] whenever there is a control-flow edge from P to B. However, since a definition cannot reach a point unless there is a path along which it reaches, w[B] needs to be no larger than the union of the reaching definitions of all the predecessor blocks. That is, it is safe to assume

We refer to union as the meet operator for reaching definitions. In any data-flow schema, the meet operator is the one we use to create a summary of the contributions from different paths at the confluence of those paths.

Iterative  Algorithm for Reaching Definitions

We assume that every control-flow graph has two empty basic blocks, an ENTRY node, which represents the starting point of the graph, and an EXIT node to which all exits out of the graph go.  Since no definitions reach the beginning of the graph, the transfer function for the ENTRY  block is a simple constant function that returns 0 as an answer.  That is, O U T [ E N T R Y ] = 0.

The reaching definitions problem is defined by the following equations:

These equations can be solved using the following algorithm. The result of the algorithm is the least fixedpoint of the equations, i.e., the solution whose assigned values to the IN ' s and OUT's is contained in the corresponding values for any other solution to the equations. The result of the algorithm below is acceptable, since any definition in one of the sets IN or OUT surely must reach the point described. It is a desirable solution, since it does not include any definitions that we can be sure do not reach.

A l g o r i t h m 9 . 1 1 :  Reaching definitions.

INPUT: A flow graph for which kills and gen_B have been computed for each block B.

OUTPUT: I N [ B ] and O U T [ B ] , the set of definitions reaching the entry and exit of each block B of the flow graph.

METHOD: We use an iterative approach, in which we start with the "estimate" OUT[JB] = 0 for all B and converge to the desired values of IN and OUT. As we must iterate until the IN ' s (and hence the OUT's) converge, we could use a boolean variable change to record, on each pass through the blocks, whether any OUT has changed. However, in this and in similar algorithms described later, we assume that the exact mechanism for keeping track of changes is understood, and we elide those details.

The algorithm is sketched in Fig. 9.14. The first two lines initialize certain data-flow values.⁴ Line (3) starts the loop in which we iterate until convergence, and the inner loop of lines (4) through (6) applies the data-flow equations to every block other than the entry. •

Intuitively, Algorithm 9.11 propagates definitions as far as they will go with-out being killed, thus simulating all possible executions of the program. Algo-rithm 9.11 will eventually halt, because for every B, OUT[B] never shrinks; once a definition is added, it stays there forever. (See Exercise 9.2.6.) Since the set of all definitions is finite, eventually there must be a pass of the while-loop during which nothing is added to any OUT, and the algorithm then terminates. We are safe terminating then because if the OUT's have not changed, the IN ' s will

not change on the next pass. And, if the IN'S do not change, the OUT's cannot, so on all subsequent passes there can be no changes.

The number of nodes in the flow graph is an upper bound on the number of times around the while-loop. The reason is that if a definition reaches a point, it can do so along a cycle-free path, and the number of nodes in a flow graph is an upper bound on the number of nodes in a cycle-free path. Each time around the while-loop, each definition progresses by at least one node along the path in question, and it often progresses by more than one node, depending on the order in which the nodes are visited.

In fact, if we properly order the blocks in the for-loop of line (5), there is empirical evidence that the average number of iterations of the while-loop is under 5 (see Section 9.6.7). Since sets of definitions can be represented by bit vectors, and the operations on these sets can be implemented by logical operations on the bit vectors, Algorithm 9.11 is surprisingly efficient in practice.

Example 9 . 1 2 : We shall represent the seven definitions d1, d2, • • • ,d>j in the flow graph of Fig. 9.13 by bit vectors, where bit i from the left represents definition d{. The union of sets is computed by taking the logical OR of the corresponding bit vectors. The difference of two sets S — T is computed by complementing the bit vector of T, and then taking the logical AND of that complement, with the bit vector for S.

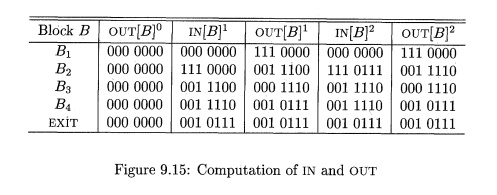
Shown in the table of Fig. 9.15 are the values taken on by the IN and OUT sets in Algorithm 9.11. The initial values, indicated by a superscript 0, as in OUTfS]0 , are assigned, by the loop of line (2) of Fig. 9.14. They are each the empty set, represented by bit vector 000 0000. The values of subsequent passes of the algorithm are also indicated by superscripts, and labeled IN [I?]1 and OUTfS]1 for the first pass and m[Bf and OUT[S]2 for the second.

 Suppose the for-loop of lines (4) through (6) is executed with B taking on the values

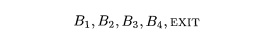
in that order. With B = B1, since OUT [ ENTRY ] = 0, [IN B1]-Pow(1) is the empty set, and OUT[P1]1 is genBl. This value differs from the previous value OUT[Si]0 , so

we now know there is a change on the first round (and will proceed to a second round).

Then we consider B = B₂    and compute

This computation is summarized in Fig. 9.15. For instance, at the end of the first pass, OUT [ 5 2 ] 1 = 001 1100, reflecting the fact that d4 and d5 are generated in B2, while d3 reaches the beginning of B2 and is not killed in B2.

Notice that after the second round, OUT [ B2 ] has changed to reflect the fact that d& also reaches the beginning of B2 and is not killed by B2. We did not learn that fact on the first pass, because the path from d6 to the end of B2, which is B3 -» B4 -> B2, is not traversed in that order by a single pass. That is, by the time we learn that d$ reaches the end of B4, we have already computed IN[B2 ] and OUT [ B 2 ] on the first pass.

There are no changes in any of the OUT sets after the second pass. Thus, after a third pass, the algorithm terminates, with the IN's and OUT's as in the final two columns of Fig. 9.15.

5. Live-Variable Analysis

Some code-improving transformations depend on information computed in the direction opposite to the flow of control in a program; we shall examine one such example now. In live-variable analysis we wish to know for variable x and point p whether the value of x at p could be used along some path in the flow graph starting at p. If so, we say x is live at p; otherwise, x is dead at p.

An important use for live-variable information is register allocation for basic blocks. Aspects of this issue were introduced in Sections 8.6 and 8.8. After a value is computed in a register, and presumably used within a block, it is not necessary to store that value if it is dead at the end of the block. Also, if all registers are full and we need another register, we should favor using a register with a dead value, since that value does not have to be stored.

Here, we  define  the  data-flow  equations  directly in  terms  of IN [5]  and OUTpB], which represent the set of variables live at the points immediately before and after block B, respectively. These equations can also be derived by first defining the transfer functions of individual statements and composing them to create the transfer function of a basic block.  Define

1.  defB    as the set of variables  defined  (i.e., definitely assigned values)  in B prior to any use of that variable in B, and useB as the set of variables whose values may be used in B prior to any definition of the variable.

Example 9 . 1 3 : For instance, block B2    in Fig. 9.13 definitely uses i. It also uses j before any redefinition of j, unless it is possible that i and j are aliases of one another.  Assuming there are no aliases among the variables in Fig. 9.13, then uses2     =  {i,j}- Also,  B2    clearly defines i  and j. Assuming there  are no aliases, defB2   =  as well.

As a consequence of the definitions, any variable in useB must be considered live on  entrance to block B, while definitions  of variables in defB     definitely are dead  at  the beginning of B.   In  effect, membership in defB "kills" any opportunity for a variable to be live because of paths that begin at B.

Thus, the equations relating def and use to the unknowns IN and OUT are defined as follows:

The first equation specifies the boundary condition, which is that no variables are live on exit from the program. The second equation says that a variable is live coming into a block if either it is used before redefinition in the block or it is live coming out of the block and is not redefined in the block. The third equation says that a variable is live coming out of a block if and only if it is live coming into one of its successors.

The relationship between the equations for liveness and the reaching-defin-itions equations should be noticed:

            Both sets of equations have union as the meet operator. The reason is that in each data-flow schema we propagate information along paths, and we care only about whether any path with desired properties exist, rather

than whether something is true along all paths.

• However, information flow for liveness travels "backward," opposite to the direction of control flow, because in this problem we want to make sure that the use of a variable x at a point p is transmitted to all points prior to p in an execution path, so that we may know at the prior point that x will have its value used.

To solve a backward problem, instead of initializing O U T [ E N T R Y ] , we initialize I N [EXIT ] . Sets I N and  O U T have their roles interchanged, and use and def substitute for gen and kill, respectively. As for reaching definitions, the solution to the liveness equations is not necessarily unique, and we want the so-lution with the smallest sets of live variables. The algorithm used is essentially a backwards version of Algorithm 9.11.

Algorithm 9 . 1 4 : Live-variable analysis.

INPUT: A flow graph with  def and use computed for each block.

OUTPUT: m[B] and O U T [ £ ] ,  the set of variables live on entry and exit of each block B of the flow graph.

METHOD: Execute the program in Fig. 9.16. •

6. Available Expressions

An expression x + y is available at a point p if every path from the entry node to p evaluates  x + y, and  after the last  such evaluation prior to reaching p, there are no subsequent assignments to x or y.5 For the available-expressions data-flow schema we say that a block kills expression x + y if it assigns (or may 5 N o te that, as usual in this chapter, we use the operator + as a generic operator, not necessarily standing for addition.

assign) x or y and does not subsequently recompute x + y. A block generates expression x + y if it definitely evaluates x + y and does not subsequently define x or y.

Note that the notion of "killing" or "generating" an available expression is not exactly the same as that for reaching definitions. Nevertheless, these notions of "kill" and "generate" behave essentially as they do for reaching definitions.

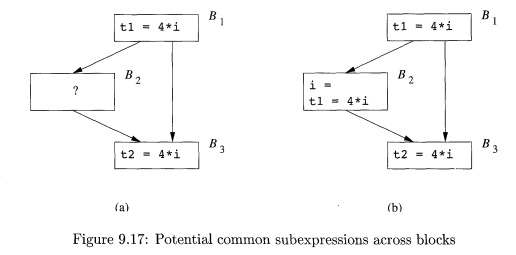
The primary use of available-expression information is for detecting global common subexpressions. For example, in Fig. 9.17(a), the expression 4 * i in block Bs will be a common subexpression if 4 * i is available at the entry point of block B3. It will be available if i is not assigned a new value in block B2, or  if, as in Fig. 9.17(b), 4 * i is recomputed after i is assigned in B2.

We can compute the set of generated expressions for each point in a block, working from beginning to end of the block. At the point prior to the block, no expressions are generated. If at point p set S of expressions is available, and q is the point after p, with statement x = y+z between them, then we form the set of expressions available at q by the following two steps.

            Add to S the expression y + z.

            Delete from S any expression involving variable x.

Note the steps must be done in the correct order, as x could be the same as y or z. After we reach the end of the block, S is the set of generated expressions for the block. The set of killed expressions is all expressions, say y + z, such that either y or z is defined in the block, and y + z is not generated by the block.

E x a m p l e 9.15 : Consider the four statements of Fig. 9.18. After the first, b + c is available. After the second statement, a — d becomes available, but b + c is no longer available, because b has been redefined. The third statement does not make b + c available again, because the value of c is immediately changed.

After the last statement, a — d is no longer available, because d has changed. Thus no expressions are generated, and all expressions involving a, b, c, or d are killed.

We can find available expressions in a manner reminiscent of the way reach-ing definitions are computed. Suppose U is the "universal" set of all expressions appearing on the right of one or more statements of the program. For each block B, let IN[B] be the set of expressions in U that are available at the point just before the beginning of B. Let OUT[B] be the same for the point following the end of B. Define e.genB to be the expressions generated by B and eJnills to be the set of expressions in U killed in B. Note that I N , O U T , e_#en, and eJkill can all be represented by bit vectors. The following equations relate the unknowns

T he above equations look almost identical to the equations for reaching definitions. Like reaching definitions, the boundary condition is OUT [ ENTRY ] = 0, because at the exit of the E N T R Y node, there are no available expressions.

The most important difference is that the meet operator is intersection rather than union. This operator is the proper one because an expression is available at the beginning of a block only if it is available at the end of all its predecessors. In contrast, a definition reaches the beginning of a block whenever it reaches the end of any one or more of its predecessors.

The use of D rather than U makes the available-expression equations behave differently from those of reaching definitions. While neither set has a unique solution, for reaching definitions, it is the solution with the smallest sets that corresponds to the definition of "reaching," and we obtained that solution by starting with the assumption that nothing reached anywhere, and building up to the solution. In that way, we never assumed that a definition d could reach a point p unless an actual path propagating d to p could be found. In contrast, for available expression equations we want the solution with the largest sets of available expressions, so we start with an approximation that is too large and work down.

It may not be obvious that by starting with the assumption "everything (i.e., the set U) is available everywhere except at the end of the entry block" and eliminating only those expressions for which we can discover a path along which it is not available, we do reach a set of truly available expressions. In the case of available expressions, it is conservative to produce a subset of the exact set of available expressions. The argument for subsets being conservative is that our intended use of the information is to replace the computation of an available expression by a previously computed value. Not knowing an expres-sion is available only inhibits us from improving the code, while believing an expression is available when it is not could cause us to change what the program computes.

Example 9 . 1 6 :  We shall concentrate on a single block,  B2    in Fig. 9.19, to illustrate the effect of the initial approximation of OUT[B2]  on IN  [ B 2 ] -  Let G and K abbreviate e.genB2 and e-killB2, respectively. The data-flow equations for block B2    are    

Algorithm 9 . 1 7 :  Available expressions.

INPUT: A flow graph with e-kills and e.gens computed for each block B. The initial block is B1.

OUTPUT: IN [5] and O U T [ 5 ] , the set of expressions available at the entry and exit of each block B of the flow graph.

METHOD: Execute the algorithm of Fig. 9.20. The explanation of the steps is similar to that for Fig. 9.14. •

Figure 9.20:  Iterative algorithm to compute available expressions

7. Summary

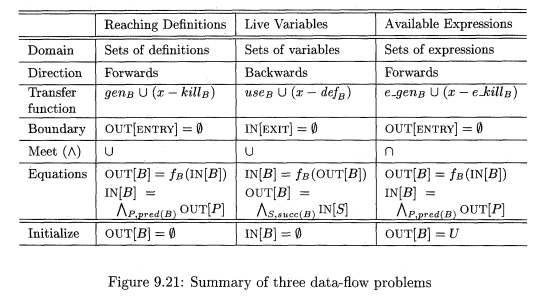
In this section, we have discussed three instances of data-flow problems: reach-ing definitions, live variables, and available expressions. As summarized in Fig. 9.21, the definition of each problem is given by the domain of the data-flow values, the direction of the data flow, the family of transfer functions, the boundary condition, and the meet operator. We denote the meet operator generically as A.

The last row shows the initial values used in the iterative algorithm. These values are chosen so that the iterative algorithm will find the most precise solution to the equations. This choice is not strictly a part of the definition of the data-flow problem, since it is an artifact needed for the iterative algorithm. There are other ways of solving the problem. For example, we saw how the transfer function of a basic block can be derived by composing the transfer functions of the individual statements in the block; a similar compositional approach may be used to compute a transfer function for the entire procedure, or transfer functions from the entry of the procedure to any program point. We shall discuss such an approach in Section 9.7.

8. Exercises for Section 9.2

Exercise 9 . 2 . 1 : For the flow graph of Fig. 9.10 (see the exercises for Sec-tion 9.1), compute

            The gen and kill sets for each block.

            The IN and O U T sets for each block.

Exercise 9 . 2 . 2 : For the flow graph of Fig. 9.10, compute the e_#en, eJkill, I N , and O U T sets for available expressions.

Exercise 9 . 2 . 3 : For the flow graph of Fig. 9.10, compute the def, use, INJ and O U T sets for live variable analysis.

! Exercise 9 . 2 . 4: Suppose V is the set of complex numbers. Which of the following operations can serve as the meet operation for a semilattice on V?

a)  Addition:         (a + ib) L (c + id) = (a + b) + i(c + d).

b)  Multiplication:          (a + ib) L (c + id) = (ac — bd) + i(ad + be).

Why the Available-Expressions Algorithm Works

We need to explain why starting all O U T ' s except that for the entry block with U, the set of all expressions, leads to a conservative solution to the data-flow equations; that is, all expressions found to be available really are available. First, because intersection is the meet operation in this data-flow schema, any reason that an expression x + y is found not to be available at a point will propagate forward in the flow graph, along all possible paths, until x + y is recomputed and becomes available again. Second, there are only two reasons x + y could be unavailable:

x + y is killed in block B because x or y is defined without a subse-quent computation of x + y. In this case, the first time we apply the transfer function  fs,  x + y  will be removed from OVT[B}.

2. x + y is never computed along some path.  Since x + y is never in OUT [ ENTRY ] , and it is never generated along the path in question, we can show by induction on the length of the path that x + y is  eventually removed from I N ' s and O U T ' s along that path. 

Thus, after changes subside, the solution provided by the iterative algo-rithm of Fig. 9.20 will include only truly available expressions.

c) Componentwise minimum: (a + ib) L (c + id) = min(«, c) + i mm(b, d).

d) Componentwise maximum: (a + ib) L (c + id) — max(a, c) + imax(6, of).

Exercise 9 . 2 . 5 :  We claimed that if a block B consists of n statements, and the ith. statement has gen and kill sets gerii and kilk, then the transfer function for block B has gen and kill sets gens and kills  given by

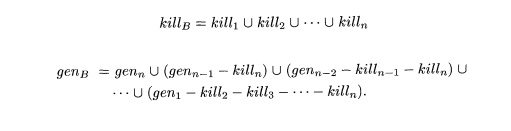
Prove this claim by induction on n.  

Exercise 9 . 2 . 6 :  Prove by induction on the number of iterations of the for-loop of lines (4) through (6) of Algorithm 9.11 that none of the IN ' s or OUT ' s ever shrinks. That is, once a definition is placed in one of these sets on some round, it never disappears on a subsequent round.

! Exercise 9 . 2 . 7 :  Show the correctness of Algorithm 9.11.  That is, show that

            If definition d is put in IN [B] or OUT[2?], then there is a path from d to the beginning or end of block B, respectively, along which the variable defined by d might not be redefined.

b)  If definition   d is not       put    in      w[B] or O U T [ . B ] , then there is no path from d to the beginning or end of block B, respectively, along which the variable defined by          d might      not    be      redefined.

Exercise 9 . 2 . 8: Prove the following about Algorithm 9.14: a) The I N ' s and OUT's never shrink.

b) If variable x is put in m[B] or 0UTp9], then there is a path from the beginning or end of block B, respectively, along which x might be used.

            If variable x is not put in IN[JB] or OUTp9], then there is no path from the beginning or end of block B, respectively, along which x might be used.

        Exercise 9 . 2 . 9 :  Prove the following about Algorithm 9.17:

            The I N ' s and OUT's never grow; that is, successive values of these sets are subsets (not necessarily proper) of their previous values.

            If expression e is removed from IN[B] or OUTpH], then there is a path from the entry of the flow graph to the beginning or end of block B, respectively, along which e is either never computed, or after its last computation, one of its arguments might be redefined.

            If expression e remains in IN[B] or OUTpB], then along every path from the

entry of the flow graph to the beginning or end of block B, respectively, e is computed, and after the last computation, no argument of e could be redefined.

        Exercise 9 . 2 . 1 0 : The astute reader will notice that in Algorithm 9.11 we could have saved some time by initializing OUTpB] to gens for all blocks B. Likewise, in Algorithm 9.14 we could have initialized m[B] to gens- We did not do so for uniformity in the treatment of the subject, as we shall see in Algorithm 9.25. However, is it possible to initialize OUTpB] to e^gens in Algorithm 9.17? Why or why not?

        Exercise 9 . 2 . 1 1 : Our data-flow analyses so far do not take advantage of the semantics of conditionals. Suppose we find at the end of a basic block a test such as

if           (x  <      10)  goto       . . .

How could we use our understanding of what the test x < 10 means to improve our knowledge of reaching definitions? Remember, "improve" here means that we eliminate certain reaching definitions that really cannot ever reach a certain program point.