Chapter: Compilers : Principles, Techniques, & Tools : Machine-Independent Optimizations
Constant Propagation
Constant Propagation
1 Data-Flow Values for the Constant-Propagation
Frame-work
2 The Meet for the Constant-Propagation Framework
3 Transfer Functions for the Constant-Propagation
Frame-work
4 Monotonicity of the Constant-Propagation
Framework
5 Nondistributivity of the Constant-Propagation
Framework
6 Interpretation of the Results
7 Exercises for Section 9.4
All the
data-flow schemas discussed in Section 9.2 are actually simple examples of
distributive frameworks with finite height. Thus, the iterative Algorithm 9.25
applies to them in either its forward or backward version and produces the MOP
solution in each case. In this section, we shall examine in detail a useful
data-flow framework with more interesting properties.
Recall
that constant propagation, or "constant folding," replaces
expressions that evaluate to the same constant every time they are executed, by
that con-stant. The constant-propagation framework described below is different
from all the data-flow problems discussed so far, in that
it has an unbounded set of possible data-flow
values, even for a fixed flow graph, and it is not distributive.
Constant propagation is a forward data-flow
problem. The semilattice rep-resenting the data-flow values and the family of
transfer functions are presented next.
1. Data-Flow Values for the
Constant-Propagation Framework
The set of data-flow values is a product lattice, with one component for
each variable in a program. The lattice for a single variable consists of the
following:
1. All constants appropriate for the type of the variable.
The value N A C , which stands for not-a-constant. A variable is mapped to
this value if it is determined not to have a constant value. The variable may
have been assigned an input value, or derived from a variable that is not a
constant, or assigned different constants along different paths that lead to
the same program point.
3. The value U N D E F , which
stands for undefined. A variable is assigned this value if nothing may yet be
asserted; presumably, no definition of the variable has been discovered to
reach the point in question.
Note that N A C and U N D E F are not the same; they are essentially opposites. N A C says we have seen so many ways a variable could be defined
that we know it is not constant; U N D E F says we have seen so little about the variable that we cannot say
anything at all.
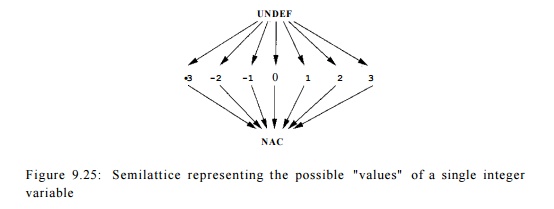
The semilattice for a typical integer-valued variable is shown in Fig.
9.25.
Here the top element is U N D E F , and the bottom element is N A C .
That is, the greatest value in the partial order is U N D E F and the least is
N A C . The constant values are unordered, but they are all less than
UNDEF and greater than NAC .
As discussed in Section 9.3.1, the meet of two values is their greatest
lower bound. Thus, for all values v,

A data-flow value for this framework is a map from each variable in the
program to one of the values in the constant semilattice. The value of a
variable v in a map m is denoted by m(v).
2. The Meet for the
Constant-Propagation Framework
The semilattice of data-flow values is simply the product of the
semilattices like Fig. 9.25, one for each variable. Thus, m < m' if and only if for all
variables v we have m(v) < m'(v).
Put another way, mAm' =
m" if m"(v) = m(v)Am'(v) for all variables v.
3. Transfer Functions for the
Constant-Propagation Framework
We assume in the following that a basic block contains only one
statement. Transfer functions for basic blocks containing several statements
can be con-structed by composing the functions corresponding to individual
statements.
The set F consists of certain transfer functions that accept a map of
variables to values in the constant lattice and return another such map .
F contains the identity function,
which takes a map as input and returns the same map as output. F also contains the constant transfer
function for the E N T R Y node. This
transfer function, given any input map, returns a map mo, where mo(v) = U N D E
F , for all variables v. This boundary condition makes sense, because
before executing any program statements there are no definitions for any
variables.
In general, let fs be the
transfer function of statement s, and let m and m' represent data-flow values
such that m' = f(m). We shall describe /s
in terms of the relationship between m and m'.
1. If s is not an assignment statement, then fs is simply the identity function.
2. If s is an assignment to variable x,
then m'(v) = m(v), for all
variables v ^ x, provided one of the
following conditions holds:
If the right-hand-side (RHS) of
the statement s is a constant c, then m'(x) = c.
(b) If the RHS is of the form y +
z, then
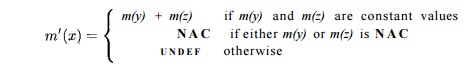
(c) If the RHS is any other expression (e.g. a function call or
assignment through a pointer), then m'(x) = N A C .
As usual, + represents a generic operator, not necessarily addition.
4. Monotonicity of the
Constant-Propagation Framework
Let us show that the constant propagation framework is monotone. First,
we can consider the effect of a function fs on a single variable. In all but case 2(b), f8 either
does not change the value of m(x), or
it changes the map to return a constant
or N A C . In these cases, /s must
surely be monotone.
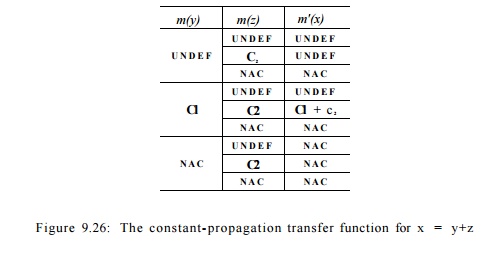
For case 2(b), the effect of fs is tabulated in Fig 9.26. The first and second columns represent the
possible input values of y and z1 the last represents the output value
of x. The values are ordered from the
greatest to the smallest in each column or sub column. To show that the
function is monotone, we check that for each possible input value of y, the value of x does not get bigger as the value of z gets smaller. For example, in the case where y has a constant value ci, as the value of z varies from U N D E F to c 2 to N A C , the value of x varies from U N D E F
, to ci + c 2 , and
then to N A C , respectively. We can repeat this
procedure for all the possible values of y. Because of symmetry, we do not even
need to repeat the procedure for the second operand before we conclude that the
output value cannot get larger as the input gets smaller.
5. Nondistributivity of the
Constant-Propagation Framework
The constant-propagation framework as defined is monotone but not
distribu-tive. That is, the iterative solution MFP is safe but may be smaller
than the MOP solution. An example will prove that the framework is not distributive.
Example 9 . 2 6 : In the program in Fig. 9.27, x and y are set to 2 and
3 in block Bi, and to 3 and 2, respectively, in block B2. We know that regardless of which path is
taken, the value of z at the end of block B3 is 5. The iterative algorithm does not discover
this fact, however. Rather, it applies
the meet operator at the entry of B3, getting as the values of x and y. Since
adding two
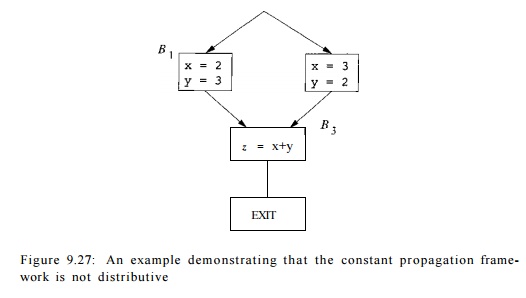
Figure 9.27: An example demonstrating that the constant propagation
frame-work is not distributive
yields a NAC, the output produced by Algorithm 9.25 is that z — NAC at the exit of the program. This
result is safe, but imprecise. Algorithm 9.25 is imprecise
because it does not keep track of the correlation that whenever x is 2, y is 3,
and vice versa. It is possible, but significantly more expensive, to use
a more complex framework that tracks all the possible equalities that hold
among pairs of expressions involving the variables in the program; this
approach is discussed in Exercise 9.4.2.
Theoretically, we can attribute this loss of precision to the
nondistributivity of the constant propagation
framework. Let f1 , f2,
and fa be
the transfer functions
representing blocks B1, B2 and B3, respectively. As shown in Fig 9.28,

6. Interpretation of the Results
The value U N D E F is used
in the iterative algorithm for two purposes: to initialize the E N T R Y node and to initialize the interior points of the program before the
iterations. The meaning is slightly different in the two cases. The first says
that variables are undefined at the beginning of the program execution; the
second says that for lack of information at the beginning of the iterative
process, we approximate the solution
with the top element UNDEF . At
the end of the iterative process, the
variables at the exit of the ENTRY node
will still hold the U N D E F value,
since OUT [ ENTRY ] never changes.
It is possible that U N D E F ' S may show up at some other program points.
When they do, it means that no definitions have been observed for that
variable along any of the paths leading up to that program point. Notice that
with the way we define the meet operator, as long as there exists a path that
defines a variable reaching a program point, the variable will not have an U N D E F value. If all the definitions reaching a program point have the same
constant value, the variable is considered a constant even though it may not be
defined along some program path.
By assuming that the program is correct, the algorithm can find more
con-stants than it otherwise would. That is, the algorithm conveniently chooses
some values for those possibly undefined variables in order to make the
pro-gram more efficient. This change is legal in most programming languages,
since undefined variables are allowed to take on any value. If the language
semantics requires that all undefined variables be given some specific value,
then we must change our problem formulation accordingly. And if instead we are
interested in finding possibly undefined variables in a program, we can
formulate a different data-flow analysis to provide that result (see Exercise
9.4.1).
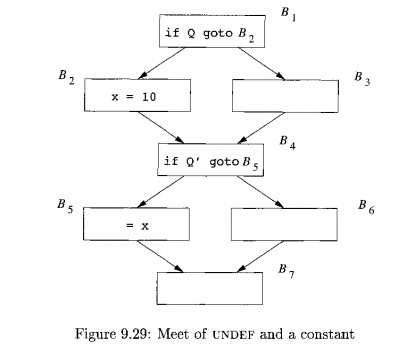
Example 9 . 2 7 : In Fig. 9.29, the values of x are 10 and U N D E F at
the exit of basic blocks B2 and B$, respectively. Since U N D E F A 10 =
10, the value of x is 10 on entry to block B4.
Thus, block B5, where x is used, can be optimized by replacing x by 10.
Had the path executed been B1 -» Bs -> B4 -» B5, the value of x reaching
basic block B5 would have been undefined. So, it appears incorrect to replace
the use of x by 10.
However, if it is impossible for predicate Q to be false while Q' is
true, then this execution path never occurs. While the programmer may be aware
of that fact, it may well be beyond the capability of any data-flow analysis to
determine. Thus, if we assume that the program is correct and that all the
variables are defined before they are used, it is indeed correct that the value
of x at the beginning of basic block B5
can only be 10. And if the program is incorrect to begin with, then choosing 10
as the value of x cannot be worse than allowing x to assume some random value.
7. Exercises for Section 9.4
Exercise 9 . 4 . 1 : Suppose we wish to detect all possibility of
a variable being
uninitialized along any path to a point where it is used. How would you
modify the framework of this section to detect such situations?
Exercise 9 . 4 . 2 : An interesting and powerful data-flow-analysis
framework is obtained by imagining the domain V to be all possible partitions of expressions, so that two
expressions are in the same class if and only if they are certain to have the
same value along any path to the point in question. To avoid having to list an
infinity of expressions, we can represent V
by listing only the minimal pairs of equivalent expressions. For example, if we
execute the statements
a = b
c = a + d
then the minimal set of equivalences is {a = 6, c = a + d}. From
these follow other equivalences, such as c = b + d and a + e = b + e,
but there is no need to list these explicitly.
a) What is the appropriate meet operator for this framework?
b) Give a data structure to represent domain values and an algorithm to
implement the meet operator.
c) What are the appropriate functions to associate with statements?
Explain the effect that a statement such as a = b+c should have on a partition
of expressions (i.e., on a value in V).
d) Is this framework
monotone? Distributive?
Related Topics