Internal Hashing

Internal Hashing

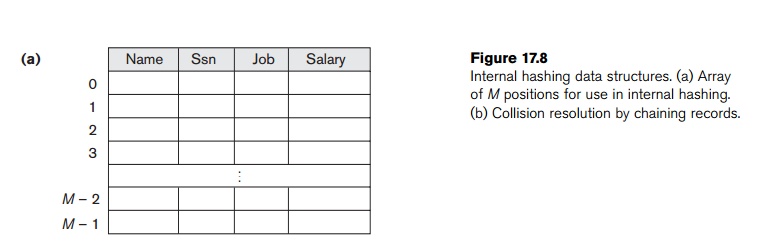
For internal files, hashing is typically implemented as a hash table through the use of an array of records. Suppose that the array index range is from 0 to M – 1, as shown in Figure 17.8(a); then we have M slots whose addresses correspond to the array indexes. We choose a hash function that transforms the hash field value into an integer between 0 and M − 1. One common hash function is the h(K) = K mod M function, which returns the remainder of an integer hash field value K after division by M; this value is then used for the record address.

Noninteger hash field values can be transformed into integers before the mod function is applied. For character strings, the numeric (ASCII) codes associated with characters can be used in the transformation—for example, by multiplying those code values. For a hash field whose data type is a string of 20 characters, Algorithm 17.2(a) can be used to calculate the hash address. We assume that the code function returns the numeric code of a character and that we are given a hash field value K of type K: array [1..20] of char (in Pascal) or char K[20] (in C).

Algorithm 17.2. Two simple hashing algorithms: (a) Applying the mod hash function to a character string K. (b) Collision resolution by open addressing.

        temp ← 1;

for i ← 1 to 20 do temp ← temp _* code(K[i ] ) mod M ; hash_address ← temp mod M;

        i ← hash_address(K); a ← i; if location i is occupied

then begin i ← (i + 1) mod M;

while (i ≠ a) and location i is occupied do i ← (i + 1) mod M;

if (i = a) then all positions are full else new_hash_address ← i;

end;

Other hashing functions can be used. One technique, called folding, involves applying an arithmetic function such as addition or a logical function such as exclusive or to different portions of the hash field value to calculate the hash address (for exam-ple, with an address space from 0 to 999 to store 1,000 keys, a 6-digit key 235469 may be folded and stored at the address: (235+964) mod 1000 = 199). Another technique involves picking some digits of the hash field value—for instance, the third, fifth, and eighth digits—to form the hash address (for example, storing 1,000 employees with Social Security numbers of 10 digits into a hash file with 1,000 positions would give the Social Security number 301-67-8923 a hash value of 172 by this hash function).⁹ The problem with most hashing functions is that they do not guarantee that distinct values will hash to distinct addresses, because the hash field space—the number of possible values a hash field can take—is usually much larger than the address space—the number of available addresses for records. The hashing function maps the hash field space to the address space.

A collision occurs when the hash field value of a record that is being inserted hashes to an address that already contains a different record. In this situation, we must insert the new record in some other position, since its hash address is occupied. The process of finding another position is called collision resolution. There are numerous methods for collision resolution, including the following:

        Open addressing. Proceeding from the occupied position specified by the hash address, the program checks the subsequent positions in order until an unused (empty) position is found. Algorithm 17.2(b) may be used for this purpose.

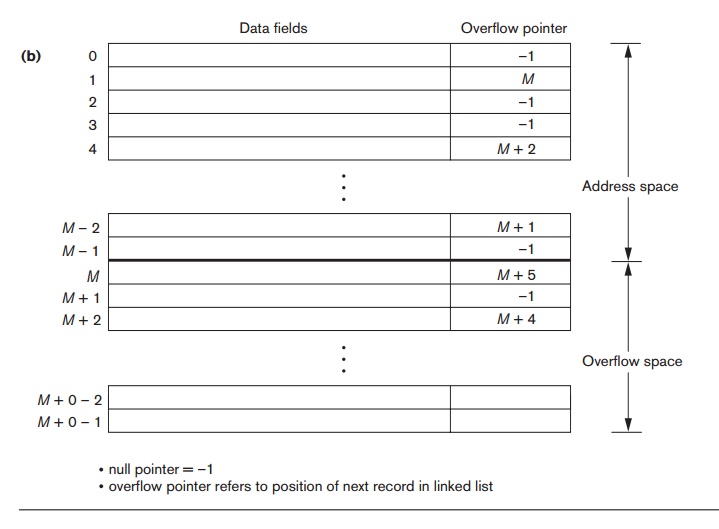
Chaining. For this method, various overflow locations are kept, usually by extending the array with a number of overflow positions. Additionally, a pointer field is added to each record location. A collision is resolved by placing the new record in an unused overflow location and setting the pointer of the occupied hash address location to the address of that overflow location.

A linked list of overflow records for each hash address is thus maintained, as shown in Figure 17.8(b).

        Multiple hashing. The program applies a second hash function if the first results in a collision. If another collision results, the program uses open addressing or applies a third hash function and then uses open addressing if necessary.

Each collision resolution method requires its own algorithms for insertion, retrieval, and deletion of records. The algorithms for chaining are the simplest. Deletion algorithms for open addressing are rather tricky. Data structures textbooks discuss internal hashing algorithms in more detail.