Chapter: Communication Theory : Random Process
Important Short Questions and Answers: Communication Theory - Random Process
RANDOM PROCESS
1. Define random variables.
A random
variable, usually written X, is a variable whose possible values are numerical
outcomes of a random phenomenon. Random variable consists of two types they are
discrete and continuous type variables.
2. What is meant by probability distribution?
The
probability distribution of a discrete random variable is a list of
probabilities associated with each of its possible values. It is also sometimes
called the probability function or the probability mass function.
3. What are the conditions applied in the central
limit theorem?
[1] The mean
of the population of means is always equal to the mean of the parent population
from which the population samples were drawn.
[2] The
standard deviation of the population of means is always equal to the standard
deviation of the parent population divided by the square root of the sample
size (N).
[3] The
distribution of means will increasingly approximate a normal distribution as
the size N of samples increases.
4. Define
stationary process.
Stationary
process is a stochastic process whose joint probability distribution does not
change when shifted in time. Consequently, parameters such as the mean and
variance, if they are present, also do not change over time and do not follow
any trends.
5.Write the equation for correlation?
The
population correlation coefficient ρX,Y between two random variables X and Y
with expected values μX and μY and standard deviations σX and σY is defined as:
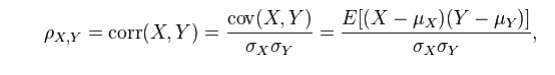
6. what is meant by covariance?
Covariance
is a measure of how much two variables change together, and the covariance
function, or kernel, describes the spatial covariance of a random variable
process or field.
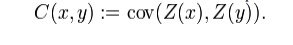
7. Define random process.
A random
process X(t) is a Gaussian process if for all n and all (t1 ,t2 ,…,tn ), the
random variables have a jointly Gaussian density function.
8. Write the equation of Autocorrelation?
The
autocorrelation function of the output random process Y (t). By definition, we
have
RY (t, u)
= E[Y (t)Y (u)]
where t
and u denote the time instants at which the process is observe
9.Write the applications of random process?
The
available noise power is directly proportional to temperature and it is
independent of value of resistance. This power specified in terms of
temperature is called as noise temperature. It is denoted by Te . It is given
as,
• Te =(F−1)T A Gaussian process can be used as
a prior probability distribution over functions in Bayesian inference.
• Wiener
process (aka Brownian motion) is the integral of a white noise Gaussian
process. It is not stationary, but it has stationary increments.
Related Topics