Stationary Process

STATIONARY PROCESS:

In mathematics and statistics, a stationary process is a stochastic process whose joint probability distribution does not change when shifted in time. Consequently, parameters such as the mean and variance, if they are present, also do not change over time and do not follow any trends.

Stationary is used as a tool in time series analysis, where the raw data is often transformed to become stationary; for example, economic data are often seasonal and/or dependent on a non-stationary price level. An important type of non-stationary process that does not include a trend-like behaviour is the cyclostationary process.

Note that a "stationary process" is not the same thing as a "process with a stationary distribution". Indeed there are further possibilities for confusion with the use of "stationary" in the context of stochastic processes; for example a "time-homogeneous" Markov chain is sometimes said to have "stationary transition probabilities". Besides, all stationary Markov random processes are time-homogeneous.

^ü   Definition:

^ü   Wide Sense Stationary:

Weaker form of stationary commonly employed in signal processing is known as weak-sense stationary, wide-sense stationary (WSS), covariance stationary, or second-order stationary. WSS random processes only require that 1st moment and covariance do not vary with respect to time. Any strictly stationary process which has a mean and a covariance is also WSS.

So, a continuous-time random process x(t) which is WSS has the following restrictions on its mean function.

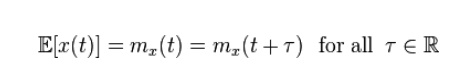
and auto covariance function.