Linear Filtering of Random Processes

LINEAR FILTERING OF RANDOM PROCESSES:

• A random process X(t) is applied as input to a linear time-invariant filter of impulse response h(t),

• It produces a random process Y (t) at the filter output as

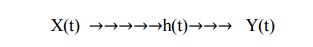
• Difficult to describe the probability distribution of the output random process Y (t), even when the probability distribution of the input random process X(t) is completely specified for −∞ ≤ t ≤ +∞.

•    Estimate characteristics like mean and autocorrelation of the output and try to analyse its behaviour.

•  Mean The input to the above system X(t) is assumed stationary. The mean of the output random process Y (t) can be calculated

where H(0) is the zero frequency response of the system.

^ü   Autocorrelation:

The autocorrelation function of the output random process Y (t). By definition, we have

RY (t, u) = E[Y (t)Y (u)]

where t and u denote the time instants at which the process is observed. We may therefore use the convolution integral to write

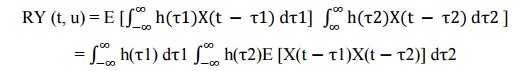
When the input X(t) is a wide-stationary random process, autocorrelation function of X(t) is only a function of the difference between the observation times t − τ1 and u − τ2.

Putting τ = t − u, we get

The mean square value of the output random process Y (t) is obtained by putting τ = 0 in the above equation.

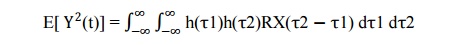
The mean square value of the output of a stable linear time-invariant filter in response to a wide-sense stationary random process is equal to the integral over all frequencies.

of the power spectral density of the input random process multiplied by the squared magnitude of the transfer function of the filter.