Covariance Functions

COVARIANCE FUNCTIONS:

In probability theory and statistics, covariance is a measure of how much two variables change together, and the covariance function, or kernel, describes the spatial covariance of a random variable process or field. For a random field or stochastic process Z(x) on a domain D, a covariance function C(x, y) gives the covariance of the values of the random field at the two locations x and y:

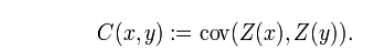
The same C(x, y) is called the auto covariance function in two instances: in time series (to denote exactly the same concept except that x and y refer to locations in time rather than in space), and in multivariate random fields (to refer to the covariance of a variable with itself, as opposed to the cross covariance between two different variables at different locations, Cov(Z(x₁), Y(x₂)))

^ü   Mean & Variance of covariance functions:

For locations x₁, x₂, …, xN ∈ D the variance of every linear combination

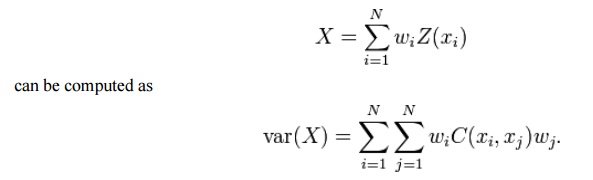
A function is a valid covariance function if and only if this variance is non-negative for all possible choices of N and weights w₁, …, w_N. A function with this property is called positive definite.